4 Складний опір

4.1 Поняття про складний опір

Під складним опором (або складним вантаженням) мають на увазі різні комбінації раніше розглянутих простих навантажених станів брусів (розтягання, стикання , зсув, кручення або згинання).

Особливо зазначають:

- одночасне згинання у двох головних площинах (складне і косе згинання);

- одночасне розтягання або стикання зі згинанням, зокрема, позацентрове розтягання-стикання;

- одночасна дія згинання і кручення з розтягуванням або без нього.

Чого-небудь принципово нового задачі складного опору при достатньо жорстких брусах не вносять, оскільки спільна дія сил призводить до напруженого стану, який може бути отриманий шляхом підсумовування напружених станів, викликаних кожним окремим видом простого вантаження. Уміючи визначити нормальні і дотичні напруження в окремих точках об'єму стрижня і знаючи способи переходу до головних напружень, можна потім, користуючись тією або іншою теорією міцності, виконати перевірку міцності даного стрижня. Аналогічно можуть бути знайдені деформації або переміщення бруса шляхом складання переміщень, що отримуються при окремих простіших навантаженнях. На практиці більшість деталей працюють в умовах складного опору.

4.1.1 Складне і косе згинання

Складним згинанням називається такий вид вантаження, при якому навантаження діють у декількох площинах, що проходить через вісь балки (рис. 4.1, а).

Якщо навантаження діють в одній площині, не співпадаючій ні з однією з головних площин, то такий вид згинання називається косим (рис. 4.1, б).

Розглянемо косе згинання стрижня (рис. 4.2), у якого плоскість згинання не збігається з головною плоскістю хz і yz.

Момент М (див. рис. 4.2) можна розкласти на дві складові за напрямками головних осей інерції перерізу:

(4.1)

де М – згинальний момент у даному перерізі в силовій плоскості р-р.

Нормальні напруження в точці з координатами x, y можна визначити сумою напружень від , використовуючи принцип суперпозиції:

(4.2)

або

(4.3)

Формули (4.2) і (4.3) дозволяють визначити нормальні напруження в будь-якій точці поперечного перерізу при складному або, як говорять ще, просторовому згинанні. Згинальний момент і координати точок, у яких визначають напруження, підставляють у формули зі своїм знаком.

Рівняння нейтральної лінії в перерізі знайдемо, вважаючи = 0 і позначаючи координати точок нейтральної лінії (н.л.) через x₀ і y₀:

(4.4)

Цим рівнянням є рівняння прямої, що проходить через початок координат (центр тяжіння перерізу), оскільки перетворюється на нуль при x₀ = y₀ = 0.

Положення нейтральної лінії характеризується її кутовим коефіцієнтом:

(4.5)

Аналіз останньої формули показує, що:

• при косому згинанні, на відміну від плоского прямого згинання, нейтральна лінія не перпендикулярна силовій лінії;

• викривлення осі бруса при косому вигині відбувається в плоскості n-n, нормальній у напрямку до нейтральної лінії (див. рис. 4.2, б); ця площина називається площиною вигину;

• напрямок площини вигину ( 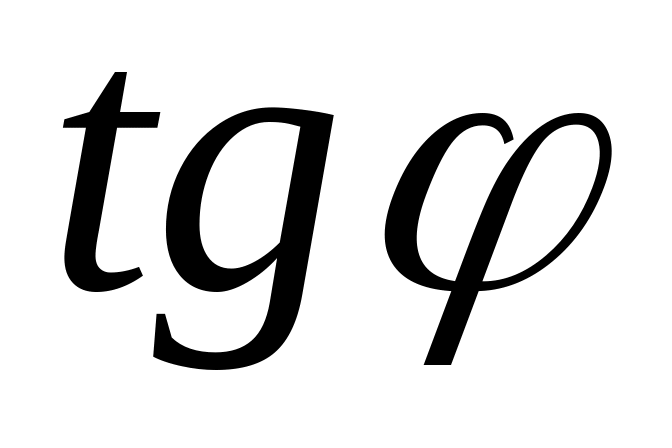) може бути перпендикулярним до площини дії зовнішнього навантаження ( ) тільки тоді, коли остання збігається з однією з головних площин бруса або коли (коло, квадрат і так далі). Загалом кут нахилу  нейтральної лінії n-n не дорівнює куту нахилу силової площині.

Оскільки епюра нормальних напружень у перерізі балки лінійна, то максимальне напруження виникає в точці, найбільш віддаленій від нейтральної лінії. Нехай координати цієї точки ( ). Тоді з рівняння (4.2) отримуємо:

(4.6)

Коли переріз симетричний відносно обох осей, визначення найбільших вантажень значно спрощується. Так, для прямокутного перерізу легко переконатися, що максимальне напруження буде завжди в кутових точках прямокутника, і для них легко записати:

або

(4.7)