2.2. Занятие 6. Магнитный поток. Электромагнитная индукция. Энергия магнитного поля
Краткие теоретические сведения
Основные формулы
Магнитный поток через плоский контур:
а) в случае однородного поля:
где
- угол между вектором нормали к плоскости
контура и вектором магнитной индукции;
- проекция вектора
на нормаль (
);
- площадь контура;
б) вслучае неоднородного поля:
где интегрирование ведется по всей поверхности .
Потокосцепление (полный магнитный поток):
где
- магнитный поток через один виток;
- число витков.
Работа по перемещению замкнутого контура с током в магнитном поле:
где
-
изменение магнитного потока, пронизывающего
поверхность, ограниченную контуром;
-
сила тока в контуре.
Разность потенциалов на концах проводника длиной , движущегося со скоростью в однородном магнитном поле с индукцией , выражается по формуле:
где - угол между направлениями векторов и .
Заряд,
протекающий по замкнутому контуру при
изменении на величину
потокосцепления, пронизывающего все
витки контура:
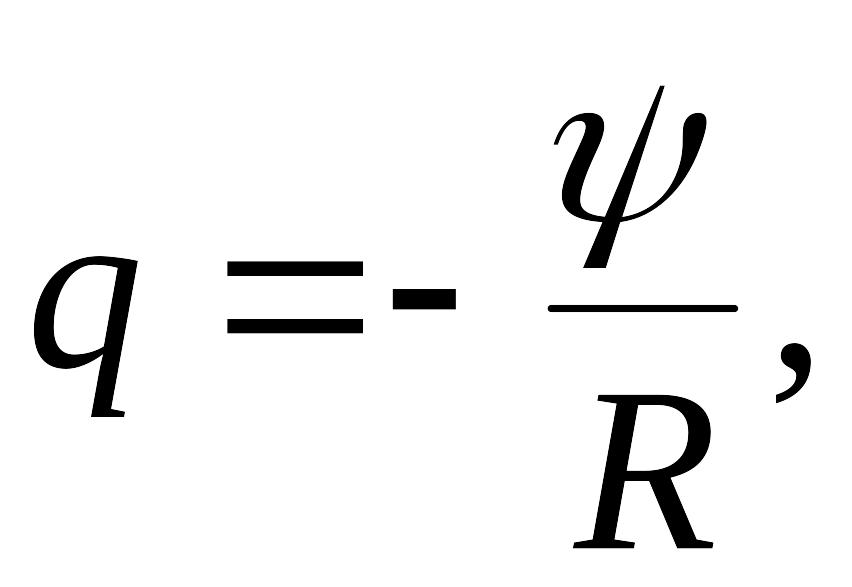
где - сопротивление контура.
Основной закон электромагнитной индукции (закон Фарадея-Максвелла):
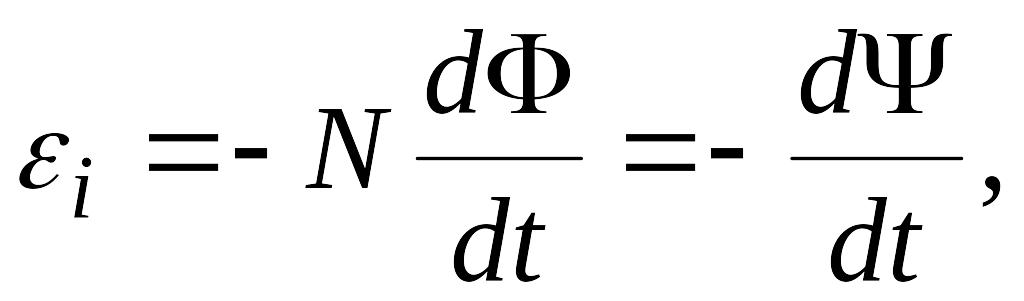
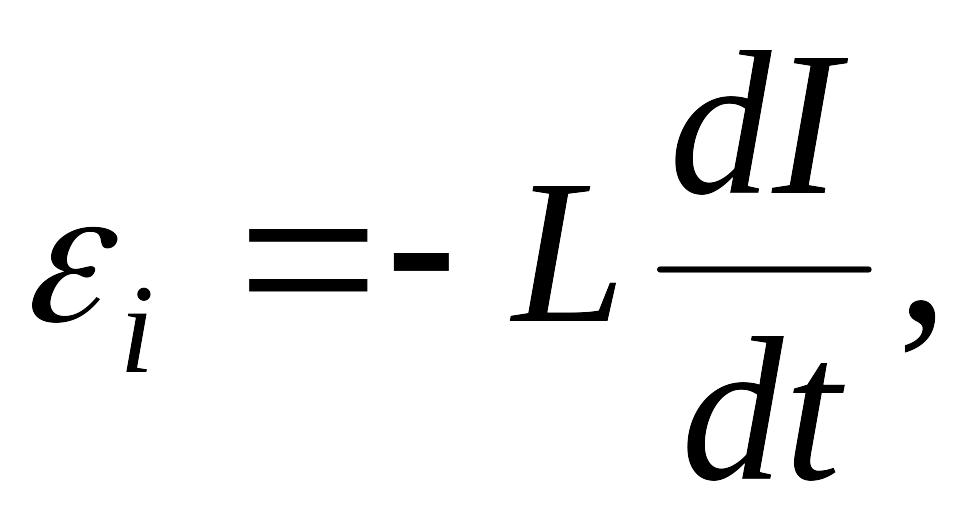
где
-
ЭДС индукции, возникающая в контуре;
- скорость изменения магнитного потока,
-
число витков контура;
- потокосцепление.
- индуктивность контура,
- скорость изменения силы тока.
Индуктивность соленоида:
где - длина соленоида, - площадь его поперечного сечения, - число витков на единицу длины.
ЭДС взаимной индукции:
где
- взаимная индуктивность контуров.
Взаимная индуктивность двух соленоидов, пронизываемых общим магнитным потоком:
где
и
- числа витков на единицу длины этих
соленоидов.
Закон изменения тока при размыкании (выключении) цепи: индуктивностью и сопротивлением :
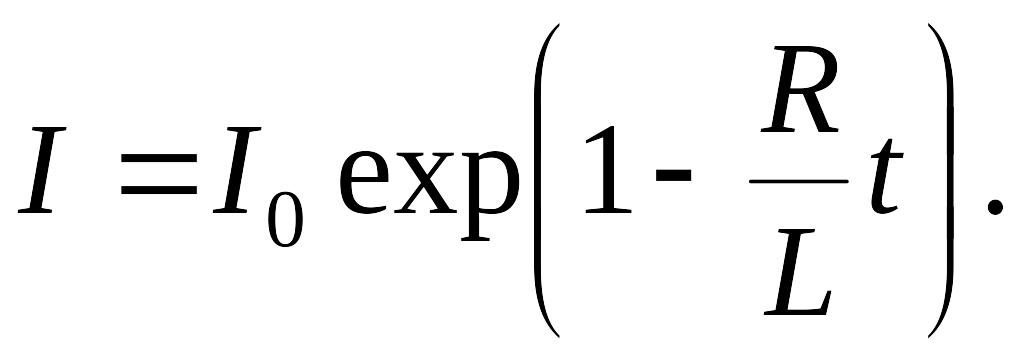
Закон изменения тока при замыкании (включении) цепи:
.
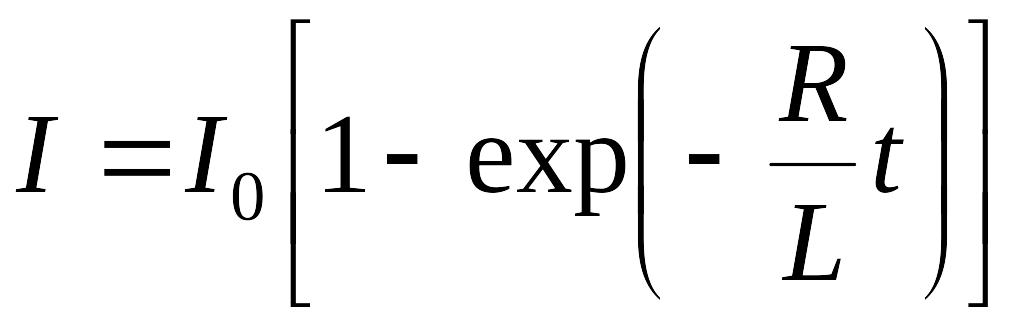Энергия магнитного поля:
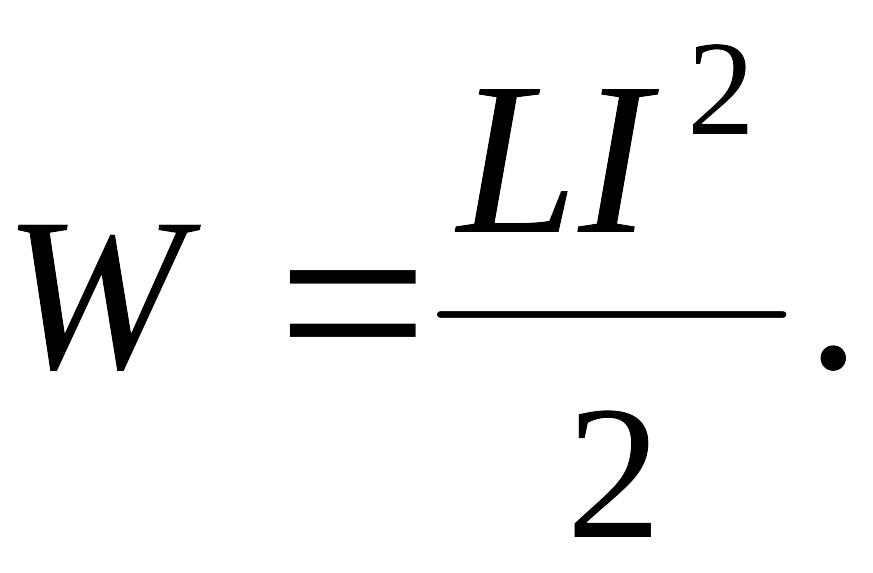
Плотность энергии магнитного поля:
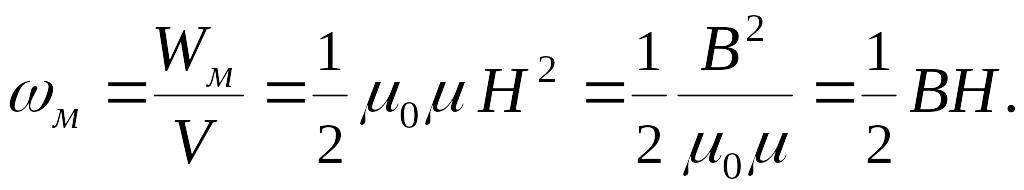
Вопросы для ответа у доски
ЭДС электромагнитной индукции.
Получите формулу для ЭДС индукции, исходя из закона сохранения энергии. Покажите, что ЭДС электромагнитной индукции возникает не только в замкнутом контуре, но и в проводнике, пересекающем при своем движении линии магнитной индукции.
Ток самоиндукции при замыкании и размыкании электрической цепи.
Нарисуйте соответствующие схемы электрических цепей, составьте дифференциальные уравнения и решите их.
Полученные результаты проанализируйте и представьте графически.
Энергия магнитного поля. Плотность энергии.
Рассчитайте работу, выполняемую до полного исчезновения магнитного поля в соленоиде при отключении источника ЭДС.
Покажите, что эта работа равна энергии магнитного поля.
Рассчитайте энергию магнитного поля бесконечного соленоида и введите в рассмотрение понятие плотности магнитной энергии.
Примеры решения задач
Задача 1.
Виток,
по которому течет ток
20А,
свободно установится в однородном
магнитном поле
16мТл.
Диаметр d
витка равен
10 см. Какую работу нужно совершать,
чтобы медленно повернуть виток на угол
/2
относительно оси, совпадающей с
диаметром?
Решение.
При медленном повороте контура в магнитном поле индукционными токами можно пренебречь и считать ток в контуре постоянным. Работа сил поля в этом случае определяется выражением:
где
и
- магнитные потоки, пронизывающие контур
в начальном и конечном положениях.
Работа внешних сил будет равна модулю работе сил поля и противоположна ей по знаку:
(*)
Момент
внешних сил, действующий
на контур, равен нулю,
так как
в начальном положении контур установился
свободно (положение
устойчивого равновесия).
В
этом положении вектор магнитного
момента
контура сонаправлен с вектором
(рис.а) и магнитный поток
максимален (
0,
1),
.
В
конечном положении (рис.б)
вектор
перпендикулярен вектору
(
/2,
0)
и магнитный поток
0.
Подставляя в (*), получаем:
где
площадь контура
С
учетом этого:
.
Подставляя числовые значения, находим:
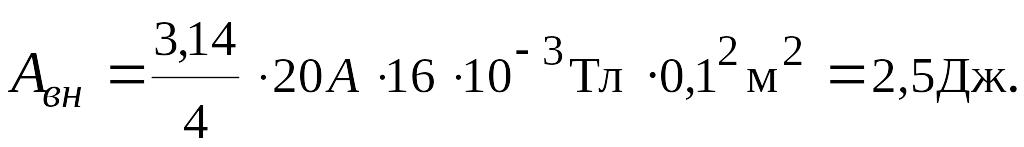
Ответ: 2,5Дж.
Задача 2.
Пусть в магнитном поле имеется замкнутый контур, пронизываемый потоком магнитной индукции . Предположим, что этот поток уменьшается до нуля. Вычислить величину заряда, прошедшего по цепи.
Решение.
Мгновенное значение ЭДС индукции в процессе исчезновения магнитного потока выражается формулой:
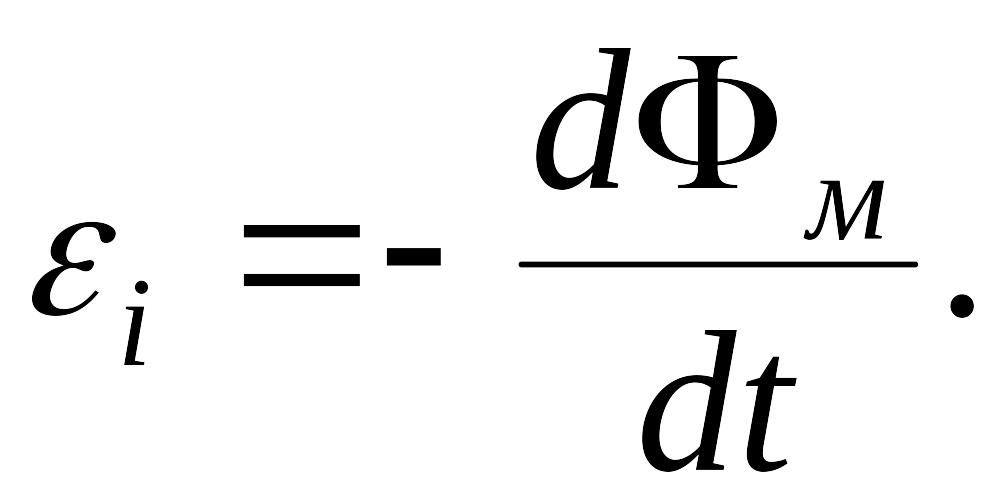
Следовательно, мгновенное значение силы тока по закону Ома будет равно:
,
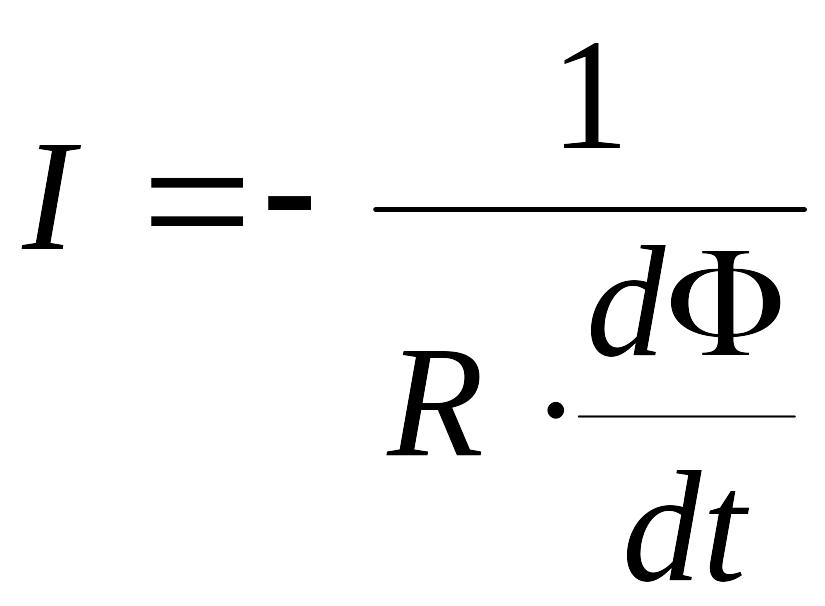где
- полное сопротивление контура.
Тогда величина прошедшего заряда:
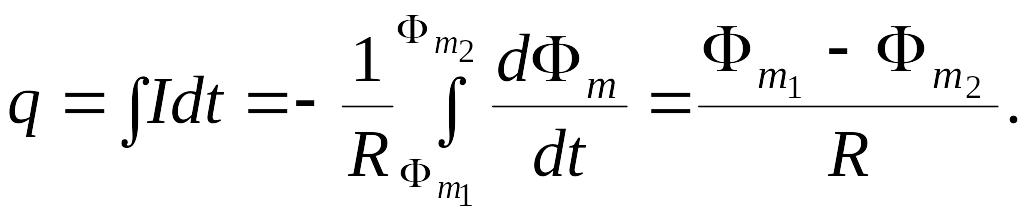
Так
как
,
то
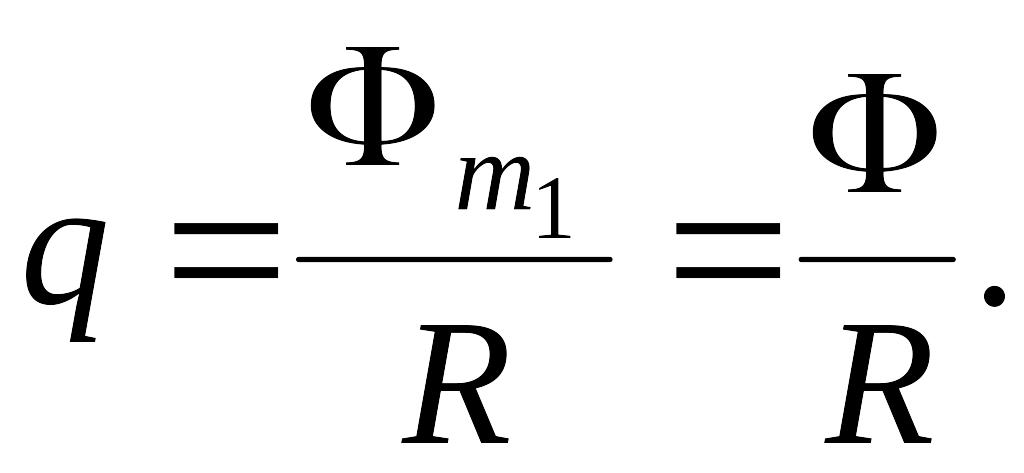
Ответ:
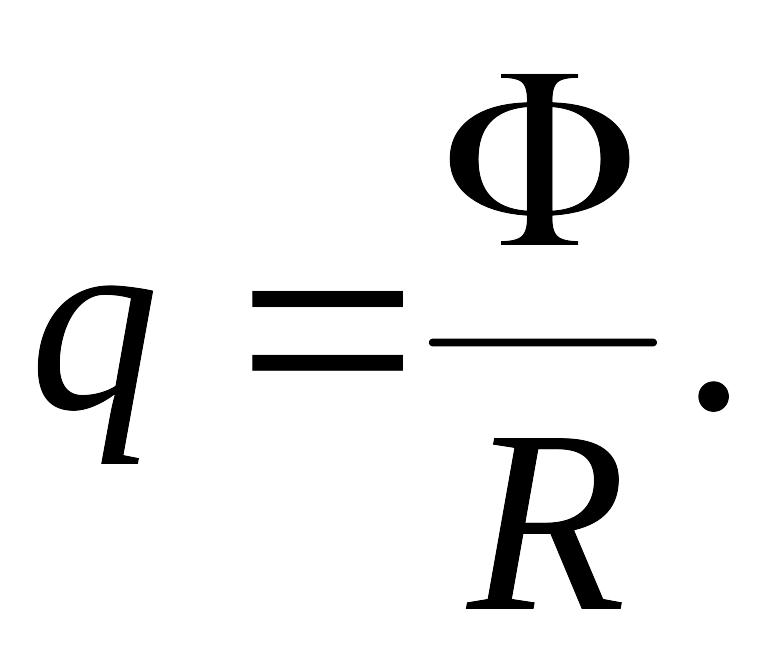
Задача 3.
В
однородном магнитном поле с индукцией
0,1Тл
равномерно вращается рамка, содержащая
1000
витков, с частотой
10с-1.
Площадь
рамки равна 150 см3.
Определить мгновенное значение ЭДС
,
соответствующее
углу поворота рамки 300.
Решение.
Мгновенное значение ЭДС индукции определяется основным уравнением электромагнитной индукции Фарадея-Максвелла:
(*)
Потокосцепление
,
где - число витков, пронизываемых магнитным потоком . Подставив выражение в (*), получим:
(**)
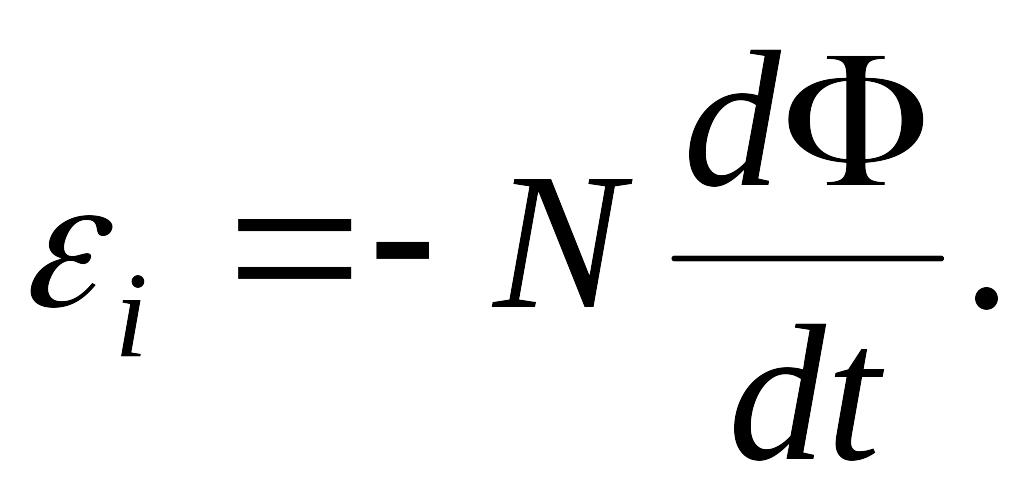При вращении рамки магнитный поток пронизывающий рамку в момент времени , изменяется по закону:
где - магнитная индукция; - площадь рамки; - угловая частота.
Подставив в формулу (**) выражение и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:
(***)
Угловая
частота
связана с частотой
вращения
соотношением
.
Подставив
выражение
в формулу (***) и заменив
на угол
,
получим:
Подставляя численные значения, находим:
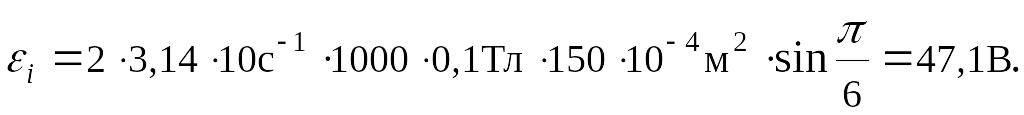
Ответ:
47,1В.
Задача 4.
Обмотка
тороида содержит
10
витков/см. Сердечник немагнитный. При
какой силе тока
плотность энергии магнитного поля
1Дж/м?
Считать, что диаметр витка обмотки
много меньше диаметра тороида.
Решение.
Силовая линия радиусом , проходящая внутри тороида охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому по закону полного тока (теорема о циркуляции):
где
- число витков в тороиде, отсюда:
(*)
-
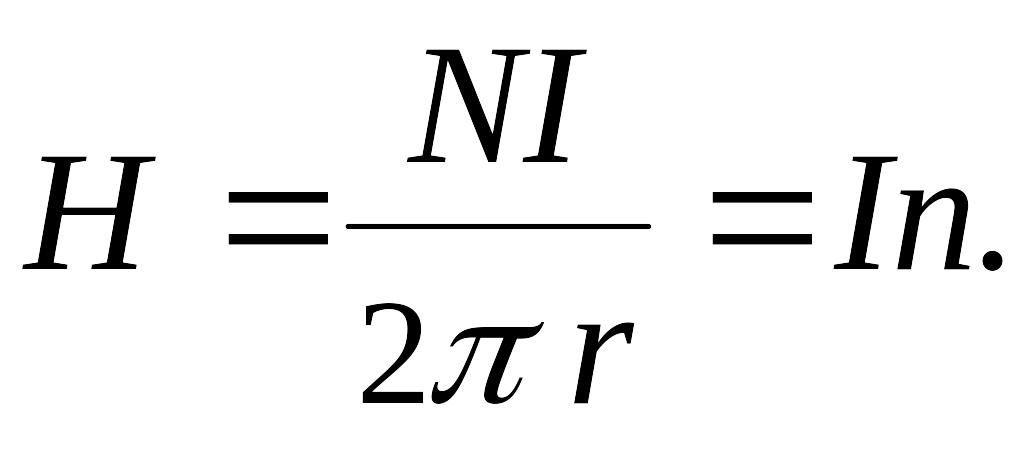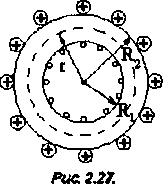
это длина окружности, определяемая
средней линией тороида. По условию
задачи обмотка тороида содержит
10
витков/см,
т.е.: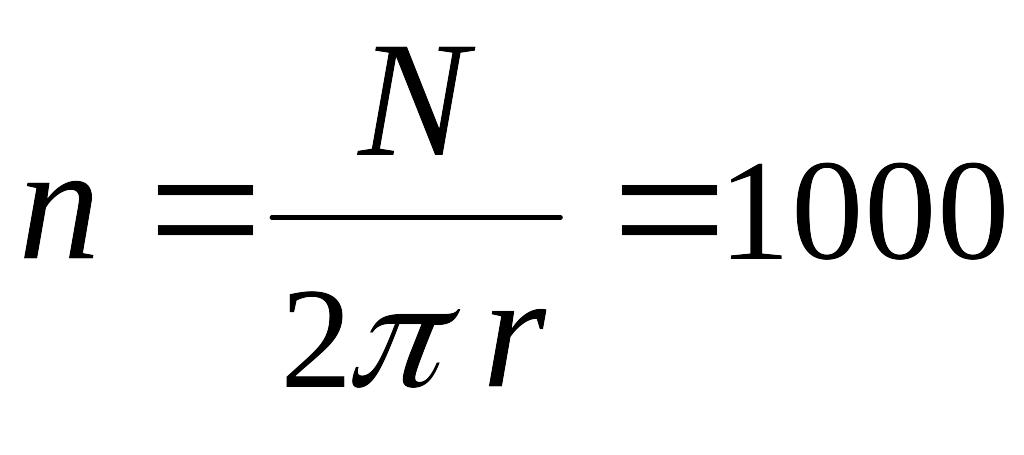
витков/м.
Объемная плотность энергии магнитного поля:
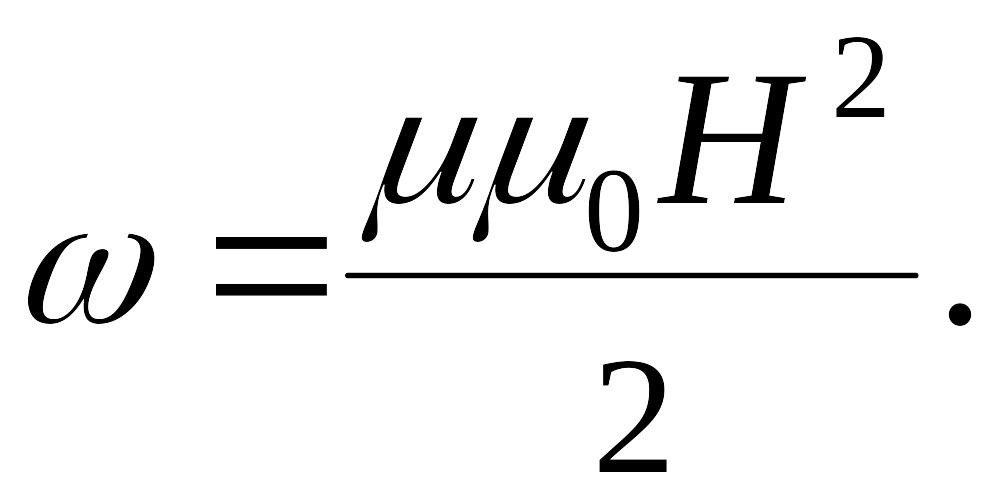
Определим
отсюда
:
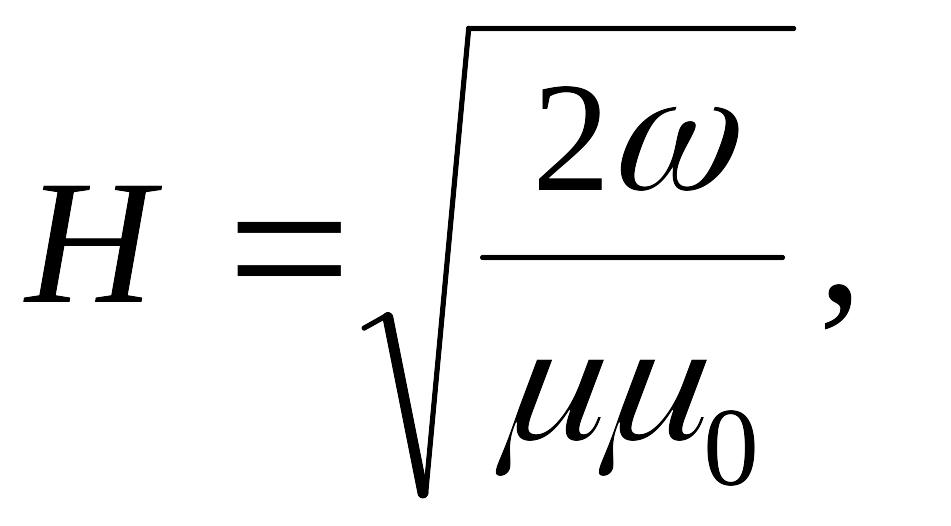согласно
(*)
Приравняв правые части, получаем:
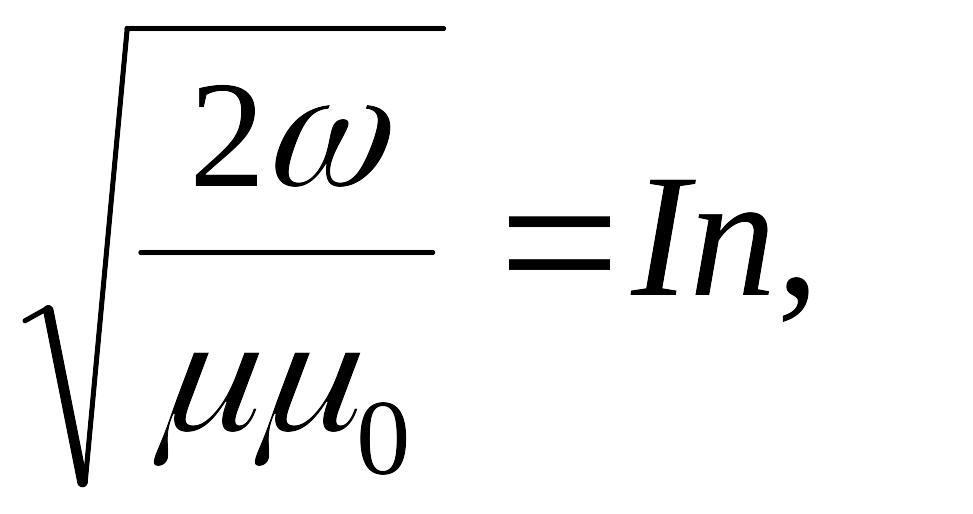отсюда: 
Подставив численные значения, находим:
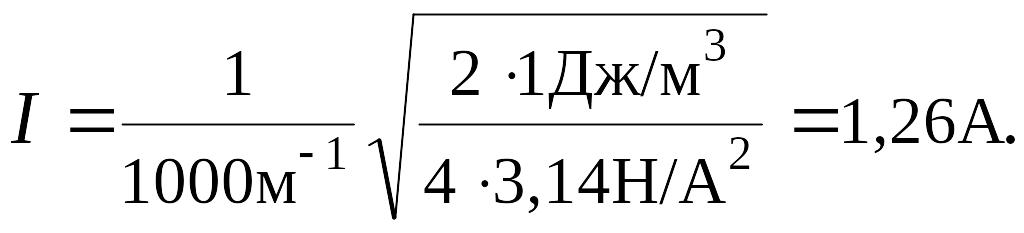
Ответ: 1,26А.
Задача 5.
Кольцо
из сверхпроводника помещено в магнитное
поле, индукция которого нарастает от
нуля до
.
Плоскость кольца перпендикулярна
линиям магнитной индукции поля.
Определите силу индукционного тока,
возникающего в кольце. Радиус кольца
равен r
, индуктивность L.
Решение.
Сопротивление
кольца равно нулю и суммарная
электродвижущая сила в нём должна быть
равна нулю. Иначе сила тока согласно
закону Ома станет бесконечной.
Следовательно, изменение магнитного
потока внешнего магнитного поля равно
по модулю и противоположно по знаку
изменению магнитного потока, созданного
индукционным током:
Учитывая, что поток
нарастает от нуля до
,
а индукционный
ток меняется при этом от 0 до I,
получим:
отсюда:
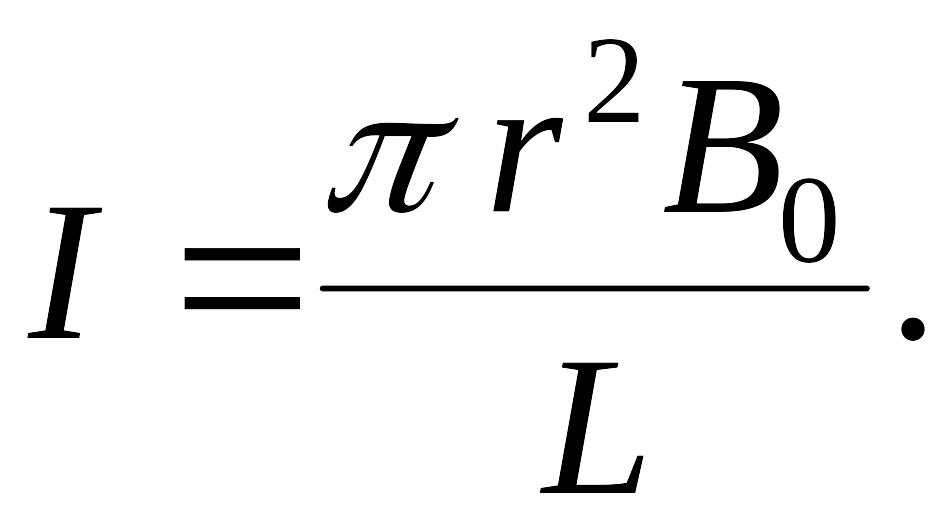
Ответ:
Задача 6.
По обмотке длинного соленоида со стальным сердечником течет ток силой 2А. Определить объёмную плотность энергии магнитного поля в сердечнике, если число витков на каждом сантиметре длины соленоида равно 7см-1.
Решение.
Объёмная плотность энергии магнитного поля найдём по формуле:
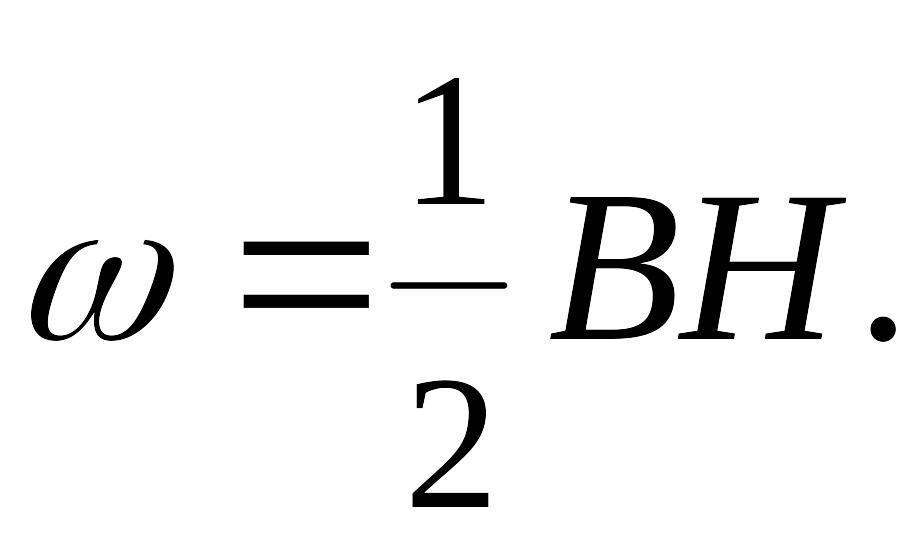
Напряженность
магнитного поля найдем как
Подставив сюда значения
(
7см-1=700м-1),
найдём:
1400А/м.
Магнитную индукцию определим по графику зависимости индукции от напряженности магнитного поля:
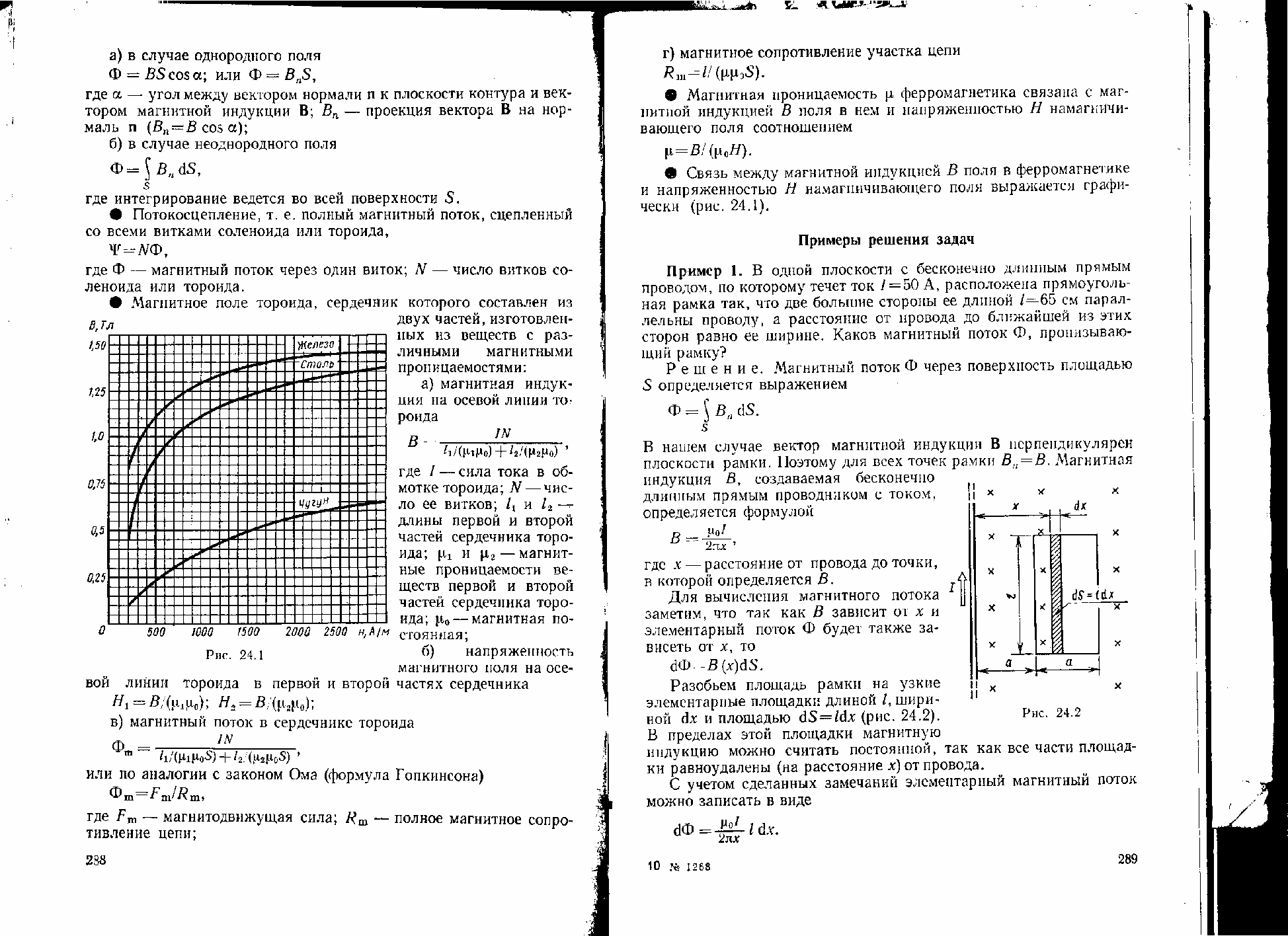
Из справочной литературы по приведенному графику: 1,2Тл.
Отсюда получаем:
840Дж.
Ответ: 840Дж.
Домашнее задание:
[Л-2] – 11.93, 11.98, 11.104, 11.108, 11.117, 11.122, 11.126, 11.128, 11.132;
[Л-3] – 3.125, 3.127, 3.132, 3.134, 3.137, 3.141;
[Л-4] – 3.183, 3.186, 3.187, 3.188, 3.195, 3.198.