
- •Гоу впо «Кемеровский государственный университет»
- •Методы вычислений
- •Предисловие
- •Тема 1. Элементы теории погрешностей
- •1.1. Определения
- •1.2. Абсолютная и относительная погрешности
- •1.3. Значащие цифры и число верных знаков
- •1.4. Погрешности арифметических действий
- •1.5. Погрешность вычисления функции
- •Задания
- •Варианты
- •Тема 2. Интерполирование
- •2.1. Постановка задачи интерполирования
- •2.2. Интерполяционный многочлен Лагранжа
- •2.3. Интерполяционная формула Гаусса
- •2.4. Сплайн- интерполяция
- •2.5. Линейный сплайн
- •Таким образом, линейный сплайн имеет вид
- •2.6. Параболический сплайн
- •2.7. Кубический сплайн
- •Задания
- •Варианты функций
- •Тема 3. Численное интегрирование
- •3.1. Постановка задачи интегрирования
- •3.2. Квадратурные формулы
- •3.3. Выбор шага интегрирования
- •3.4. Квадратурная формула Гаусса
- •Тогда формула Гаусса будет иметь вид
- •Задания
- •Варианты
- •Тема 4. Решение трансцендентных (нелинейных) уравнений
- •4.1. Отделение корней
- •4.2. Метод последовательных приближений (метод простой итерации)
- •4.3. Метод половинного деления (метод проб, метод дихотомии)
- •4.4. Метод пропорционального деления (метод хорд)
- •4.5. Метод Ньютона (метод касательных)
- •4.6. Метод Ньютона модифицированный
- •4.7. Метод Чебышева
- •Задания
- •Варианты уравнений
- •Тема 5. Решение спектральной задачи
- •5.1. Метод скалярных произведений
- •5.2. Метод вращения
- •Задания
- •Варианты матриц
- •Тема 6. Решение систем линейных алгебраических уравнений
- •6.1. Обусловленность матрицы
- •6.2. Метод Гаусса
- •6.3. Метод Гаусса с выбором главного элемента
- •6.4. Нахождение определителя и обращение матрицы с помощью метода Гаусса
- •6.5. Итерационные методы (метод Якоби, метод Зейделя, метод релаксации)
- •6.6. Оптимизация скорости сходимости итерационного процесса
- •6.7. Итерационные методы вариационного типа
- •6.8. Методы сопряженных направлений
- •Задания
- •Тема 7. Решение систем нелинейных алгебраических уравнений
- •7.1. Определения
- •Интеграл в правой части (8.4) вычисляется с помощью численной квадратуры
- •8.2. Метод Эйлера
- •8.3. Методы Рунге-Кутта
- •8.4. Метод Адамса
- •8.5. Метод Милна
- •Задания
- •Варианты
- •8.6. Краевая задача для обыкновенного дифференциального уравнения второго порядка
- •8.6.1. Интегро-интерполяционный метод
- •8.6.2. Метод прогонки
- •Задания
- •Варианты заданий
- •Тема 9. Методы решения дифференциальных уравнений в частных производных
- •9.1. Простейшие приемы построения разностных схем
- •9.2. Сходимость, аппроксимация, устойчивость разностных схем
- •9.3. Решение уравнения параболического типа
- •9.3.1. Явная разностная схема
- •9.3.2. Неявная разностная схема
- •9.3.3. Реализация метода разностной прогонки для уравнения параболического типа
- •Задание
- •Варианты
- •9.4. Решение уравнения эллиптического типа
- •9.4.1. Метод матричной прогонки
- •Задание:
- •Варианты
- •Содержание
- •Тема 7. Решение систем нелинейных алгебраических уравнений 40
- •Тема 8. Решение обыкновенных дифференциальных уравнений 43
- •Тема 9. Методы решения дифференциальных уравнений в частных производных 49
Задания
С помощью метода скалярных произведений найти максимальное по модулю и минимальное по модулю собственное значение и соответствующие им собственные вектора для симметричной матрицы A с заданной точностью ε. Провести расчеты при различных начальных приближениях x(0).
С помощью метода вращения найти все собственные значения и соответствующие им собственные вектора для симметричной действительной матрицы A с заданной точностью ε.
Варианты матриц
1.
 2.
2.
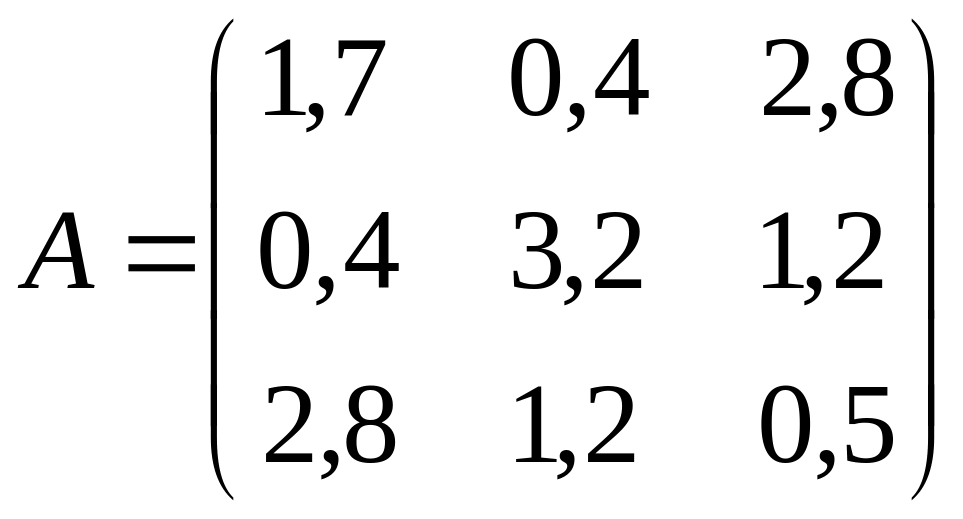
3.
 4.
4.

5.
 6.
6.
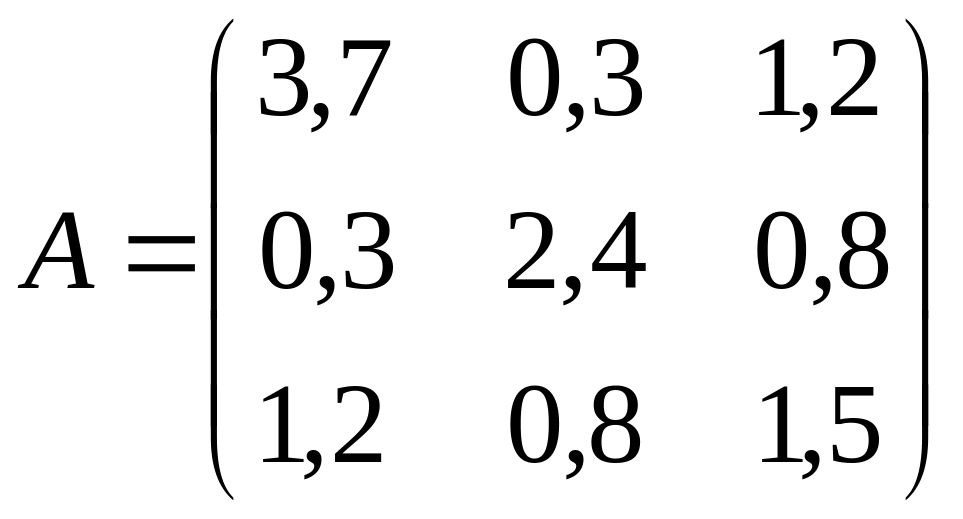
7.
 8.
8.

9.
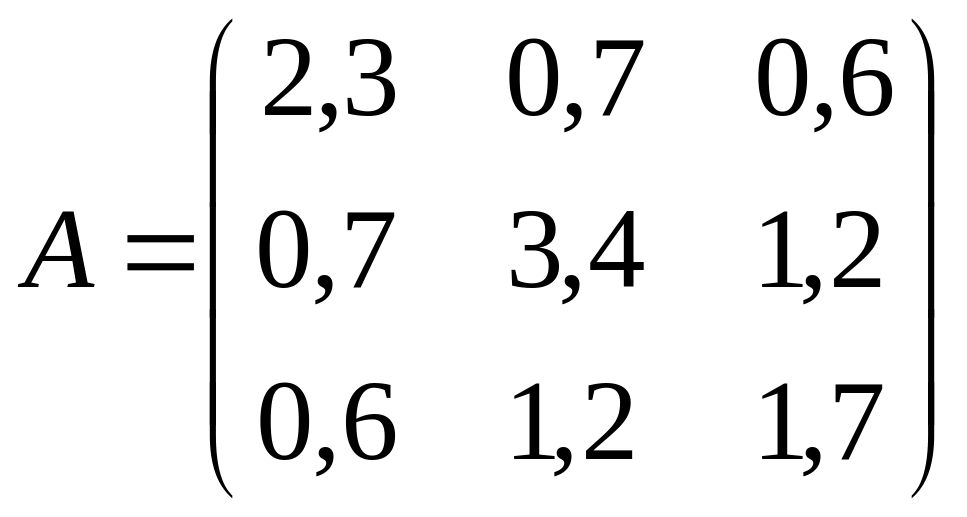 10.
10.

11.
 12.
12.

13.
 14.
14.

15.
 16.
16.

17.
 18.
18.

19.
 20.
20.

Тест: 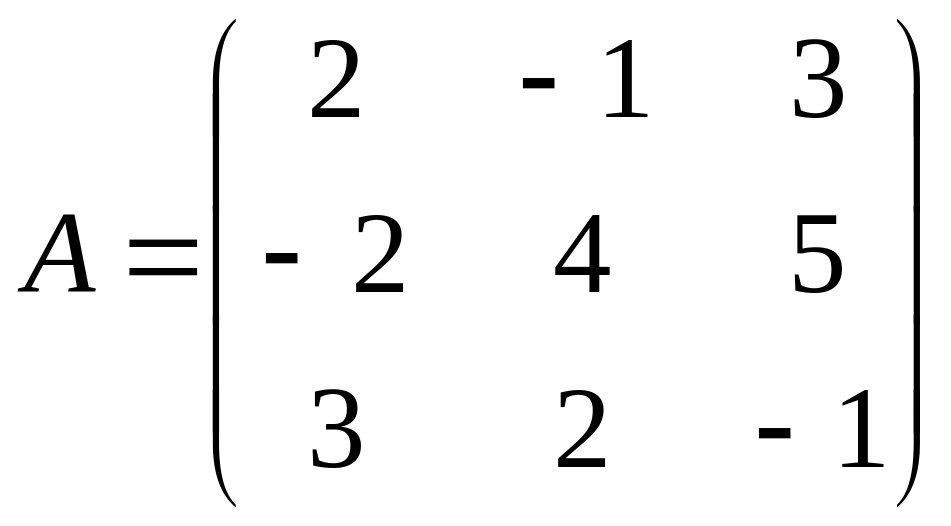 ,
,
λ 1= -4,2841, x1 = (-0,597; -0,746; 1),
λ2 = 3,7621, x 2= (1; -0,492; 0,423),
λ3 = 5,522, , x 3= (-0,00858; 0,228; 1).
Тема 6. Решение систем линейных алгебраических уравнений
6.1. Обусловленность матрицы
При исследовании численных методов для решения математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма. Для каждой математической задачи принято рассматривать вопрос о ее корректности.
Определение. Говорят, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от входных данных.
Рассмотрим систему
A x = f , (6.1)
где А - квадратная, неособенная матрица размерности n, и, следовательно, det(A) ≠ 0, тогда существует единственное решение системы. Чтобы убедиться в корректности задачи (6.1) необходимо еще установить непрерывную зависимость решения от входных данных. Входными данными являются правая часть f и элементы матрицы А.
Соответственно, различают устойчивость по правой части, когда возмущается только правая часть f , а матрица А остается неизменной, и коэффициентную устойчивость, когда возмущается только матрица А .
Будем считать, что решение и правая часть задачи (6.1) принадлежат линейному пространству H, состоящему из n-мерных векторов. Введем в H норму, для которой выполнено:
||x||>0, для всех х≠0 H ,
||α x||=| α| ||x||, для любого числа А и х H ,
||x+y||≤||x||+||y||, для любых x и y H .
Определение.
Нормой матрицы А,
подчиненной данной норме векторов,
называется число
![]() ,
для всех х≠0
H
.
,
для всех х≠0
H
.
Наряду с системой (6.1) рассмотрим «возмущенную» систему A xε = fδ , которая отличается от (6.1) правой частью. Насколько сильно может измениться решение х в результате изменения правой части?
Обозначим δx=x - xε,, δf=f - fδ.
Определение. Говорят, что система (6.1) устойчива по правой части, если при любых f и fδ справедлива оценка || δx||≤ M || δf ||, где M - постоянная, M >0.
Эта оценка выражает факт непрерывной зависимости решения от правой части, то есть показывает, что || δx|| стремится к нулю при || δf ||стремящемся к нулю. Наличие устойчивости очень важно при численном решении систем уравнений, так как никогда нельзя задать правую часть f точно. Погрешность δf возникает в результате округления.
Получим
оценку для относительной погрешности
решения
![]() . Используем неравенство ||f||
≤ ||A||
||x||
. Перемножим его с неравенством
||δx||≤ ||A-1||
|| δf
||, получим
требуемую оценку
. Используем неравенство ||f||
≤ ||A||
||x||
. Перемножим его с неравенством
||δx||≤ ||A-1||
|| δf
||, получим
требуемую оценку
![]() .
.
Определение.
Число ρ(A)=![]() называется числом обусловленности
матрицы A
и характеризует степень зависимости
относительной погрешности решения от
относительной погрешности правой части.
В случае самосопряженной матрицы A
=A*
это число равно
называется числом обусловленности
матрицы A
и характеризует степень зависимости
относительной погрешности решения от
относительной погрешности правой части.
В случае самосопряженной матрицы A
=A*
это число равно
ρ(A)=![]() ,
,
где λmax , λmin – максимальное и минимальное по модулю собственные значения матрицы A.
Матрицы с большим числом обусловленности называются плохо обусловленными. При численном решении систем с такими матрицами возможно сильное накопление погрешности. При небольших изменениях правой части погрешность решения может оказаться значительной.
Например, для матрицы
![]()
число
обусловленности ρ(A)=![]() ,
и если взять
за правую часть системы вектор f=
(1,0000, 1,0000)T,
то получим решение x=(0,3333,
0,0000)T.
Решение «возмущенной» системы с правой
частью fδ
=
(0,9998, 1,0000)T
равно xε=(5,0000,
2,0000)T.
,
и если взять
за правую часть системы вектор f=
(1,0000, 1,0000)T,
то получим решение x=(0,3333,
0,0000)T.
Решение «возмущенной» системы с правой
частью fδ
=
(0,9998, 1,0000)T
равно xε=(5,0000,
2,0000)T.
Если взять матрицу
![]()
и
за правую часть системы вектор f=
(1,0000, 0)T,
то получим решение
![]() .
Решение «возмущенной» системы при
изменении коэффициента a22
= 0,421 на
0,433 равно xε
= (47,983,
-86,879)T.
.
Решение «возмущенной» системы при
изменении коэффициента a22
= 0,421 на
0,433 равно xε
= (47,983,
-86,879)T.
