6.1. Производная по заданному направлению

Начнём с рассмотрения конкретного примера. Для функции

частные производные равны .

В точке P₀(1,2,3) частные производные принимают значения

, , .

Эти три числа являются характеристиками быстроты изменения функции.

Именно из равенства заключаем о том, что функция u в точке P₀ в направлении оси Ox возрастает быстрее, чем x в 23 раза.

Из равенства заключаем, что функция u в направлении оси Oy, в точке P₀ возрастает быстрее, чем y в 16 раз.

Наконец равенство говорит о том, что в направлении оси Oz, в точке P₀ функция u в 34 раза возрастает быстрее, чем z.

Однако, часто бывает нужно знать, как быстро изменяется функция в некоторой точке P₀ по направлению, которое не параллельно направлениям координатных осей Оx, Оy, Оz.

Для ответа на поставленный вопрос нужно ввести новое понятие – понятие производной по заданному направлению в данной точке.

Прежде чем дать определение производной по заданному направлению, напомним, что направление в данной точке P₀(x₀,y₀,z₀) задается тремя углами , которые образует прямая, проходящая через точку P₀(x₀,y₀,z₀), соответственно с координатными осями Ox, Oy, Oz (книга 2, гл.4, §3, п.3.3). Эти три угла однозначно определяют в точке P₀ направление и поэтому, в дальнейшем заданное направление в точке P₀ будем записывать, коротко следующим образом: .

6.1.1. Определение производной по заданному направлению

Пусть функция

(4.36)

задана в трехмерной области D и P₀(x₀,y₀,z₀) есть внутренняя точка в D. Зададим в точке P₀ некоторое направление (рис.31) и выберем на нём точку P(x,y,z). При переходе из точки P₀ в точку P функция (4.36) получает приращение, равное . Разделим это приращение функции на расстояние между точками P и P₀ и рассмотрим отношение

Рис. 31 нанести точки

Определение. Производная по заданному направлению от функции в точке P₀(x₀,y₀,z₀), обозначается , есть предел выражения когда , причём так, что точка P(x,y,z) стремится к точке P₀(x₀,y₀,z₀), оставаясь на направлении , если этот предел существует и конечен, т.е.

. (4.37)

6.1.2. Существование и способ вычисления производной по заданному направлению

Существование и способ вычисления производной по заданному направлению устанавливается следующей теоремой.

Теорема. Для существования производной по любому заданному направлению в точке P₀(x₀,y₀,z₀) от функции , достаточно, чтобы эта функция была дифференцируемой в точке P₀, причём справедливо равенство

.

Для доказательства возьмём на произвольном направлении , выходящем из точки P₀(x₀,y₀,z₀), ещё одну точку и обозначим через расстояние между ними.

Составим полное приращение функции

.

В силу предположенной дифференцируемости функции в точке P₀, получаем

= + ερ.

Деля обе части последнего равенства на , находим

.

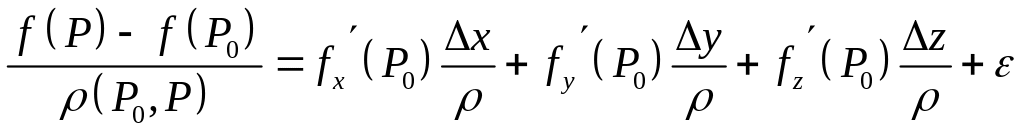Поскольку (см. книга 2, гл.4, §3, п.3.3) этому равенству можно придать следующий вид

. (4.38)

Когда и при этом точка P остаётся на направлении , то в правой части (4.38) первые три члена остаются постоянными, а слагаемое ε стремится к нулю: . Но это означает, что правая часть (4.38) при условии (точка P остаётся на направлении ) имеет предел равный , а поэтому при этих условиях существует предел в левой части (4.38) и

.

Следовательно, в согласии с определением, в точке P₀ существует производная по заданному направлению и справедливо равенство

или что то же самое

. (4.39)

Теорема доказана.

Рассмотрим частные случаи применения формулы (4.39).

Направление в точке P₀(x₀,y₀,z₀) параллельно положительному направлению оси Ox. Поэтому, , , и формула (4.39) принимает вид .

Если в точке P₀ рассмотреть направление , то оно параллельно положительному направлению оси Oy и тогда формула (4.39) даёт .

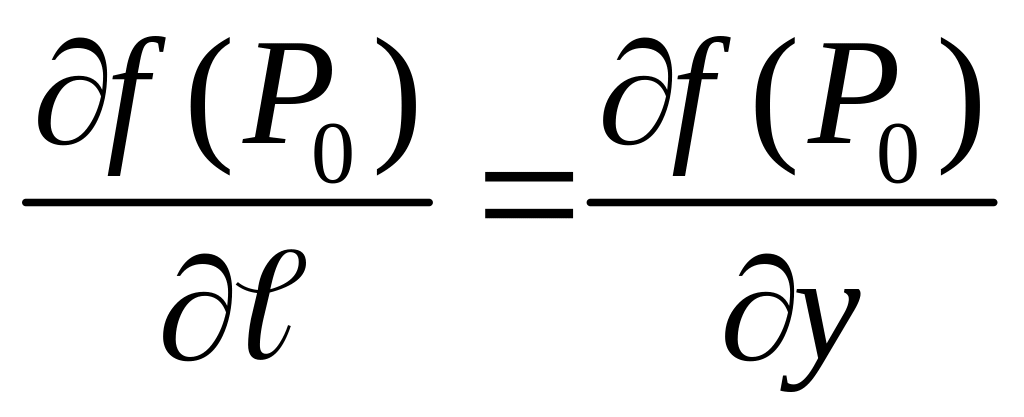Наконец, если в точке P₀ направление задано углами , то .

Из изложенного следует, что понятие производной по заданному направлению является обобщением понятия частной производной и никаких других новых формул дифференцирования для нахождения производной по заданному направлению кроме умения находить частные производные и формулы (4.39) не требуется.