157

Глава 3

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ЧИСЛОВЫХ ФУНКЦИЙ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО

Основной предмет дифференциального исчисления составляет вычисление производной, изучение и использование ее свойств.

§1. Производная числовой функции одного действительного переменного

1.1. Определение производной. Ее физическая и геометрическая интерпретация

Пусть функция определена на числовом промежутке P. Исходя из некоторого значения x = x₀ независимой переменной, придадим ему приращение ∆x, не выводящее его из промежутка P так, что и новое значение x₀ + ∆x принадлежит этому промежутку. Тогда значение y₀ = f(x₀) функции заменится новым значением y₀ + ∆y = f (x₀ + x), т.е. получит приращение

∆y = ∆ f (x₀) = f (x₀ + x) – f (x₀) или y = y – y₀.

Считая x  0, рассмотрим в данной фиксированной точке x₀ отношение приращения ∆y функции в этой точке к соответствующему приращению аргумента ∆x:

. (3.1)

Отношение (3.1) представляет собой функцию аргумента ∆x, и мы имеем право, рассматривать вопрос о существовании предела указанной функции при ∆x  0.

Определение. Если существует предел отношения приращения функции ∆y к вызвавшему его приращению независимой переменной ∆x при стремлении ∆x к нулю, т.е. 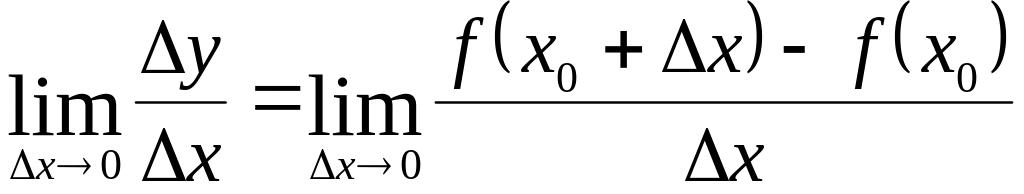, то он называется производной функции по независимой переменной x при данном ее значении (или в данной точке) x = x₀.

Таким образом, производная при данном значении x = x₀ – если существует – есть определенное число, которое будем обозначать (x₀) или (x₀). Итак, по определению,

. (3.2)

Если функция имеет производную для всех х из промежутка Р, то эта производная будет представлять собой некоторую числовую функцию переменной х, также определенную на промежутке Р. Следует заметить, что функция (x) на промежутке Р может быть как непрерывной, так и разрывной функцией.

С физической точки зрения производная определяет мгновенную скорость движущегося тела в конкретный момент времени. Если слово «скорость» понимать в общем смысле, то производную можно трактовать как некую «скорость» протекания физического процесса, который описывается функцией , по отношению к изменению переменной (параметра) х. Например: скорость нагревания или охлаждения тела (т.е. изменение температуры) по отношению к его деформации (изменению объема); скорость изменения плотности вещества по отношению к изменению его температуры; скорость изменения электроемкости плоского конденсатора по отношению к изменению либо расстояния между прокладками, либо заряда на пластинах конденсатора и т.п.

С геометрической точки зрения значение производной (x₀) при данном значении аргумента x = x₀ равняется тангенсу угла, образованного с положительным направлением оси Oх касательной к графику функции f(x) в соответствующей точке М₀ (x₀ , f`(x₀)) (рис.14).

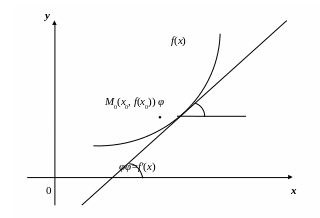
Рис. 14

Уравнение касательной y = kx+b к кривой y = f`(x) в точке М<sub>0</sub> (x<sub>0</sub>, f`(x₀)) определяется выражением:

y = (x₀) (x – x₀) + f`(x₀). (3.3)

1.2. Вычисление производных для основных элементарных функций Операция нахождения производной функции называется дифференцированием функции.

1. Отметим, прежде всего, очевидные результаты, если у = с = const, то Δу = 0, каково бы ни было Δх, так что = 0; если же у = х, то Δу = Δх и = 1.