2.3. Достаточные условия дифференцируемости функции многих переменных

Для того чтобы установить достаточные условия дифференцируемости функции многих переменных докажем прежде теорему вспомогательного характера. Для упрощения записей можно ограничиться случаем функции от трех переменных.

Теорема 1 (формула конечных приращений). Пусть функция f(x,y,z) имеет частные производные по всем трем аргументам, как в самой точке , так и в некоторой окрестности этой точки.

Тогда справедливо равенство (формула конечных приращений)

(4.11)

причем .

Для доказательства, преобразуем полное приращение функции, прибавляя и вычитая две пары одинаковых слагаемых

(4.12)

Преобразуем каждую квадратную скобку с помощью теоремы Лагранжа (гл.3, §4, п.4.2) для функции одной переменной

причем здесь .

Подставляя найденные значения разностей в (4.12), получим равенство (4.11). Теорема доказана. Эта теорема без затруднений переносится на случай функции от любого числа аргументов.

Теорема 2 (достаточное условие дифференцируемости функции многих переменных). Для того чтобы функция f(x,y,z) была бы дифференцируемой в точке достаточно, чтобы для этой функции существовали частные производные по всем ее аргументам как в самой точке P₀, так и в некоторой ее окрестности и, кроме того, чтобы все эти частные производные были непрерывны в точке P₀.

Доказательство. Дадим аргументам приращения и составим в соответствие с формулой конечных приращений (4.11) полное приращение функции

,

. На основании предположений о непрерывности частных производных в точке P₀ при условии, что 0, получаем

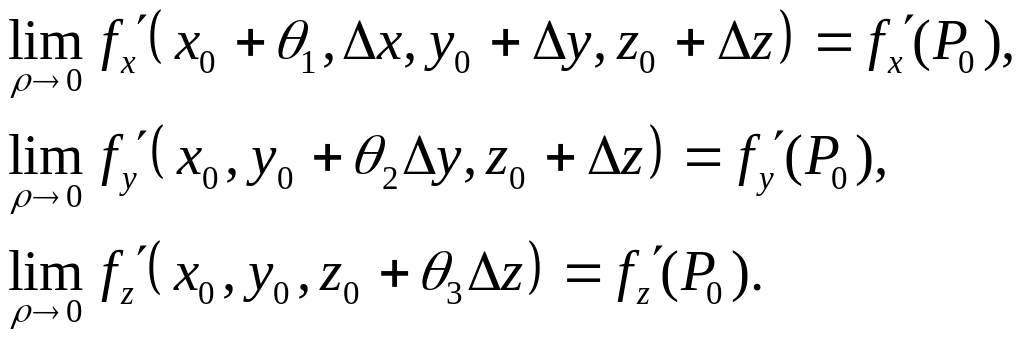
Эти предельные равенства можно записать в равносильной форме следующим образом

. (4.13)

Причем здесь

, , . (4.14)

Теперь подставляя (4.13) в (4.11) находим, что

. (4.15)

Из равенств (4.15) и (4.14), а также из теоремы 2 (§2, п.2.1) следует, что функция f(x,y,z) дифференцируема в точке . Теорема доказана.

§3. Касательная плоскость и нормаль к поверхности. Геометрическое значение полного дифференциала

Рассмотрим поверхность S заданную уравнением

z_пов. = f(x,y). (4.16)

Пусть эта поверхность проектируется на плоскость хОу в виде некоторой области D. Предполагаем, что функция f(x,y) в области D непрерывна и пусть точка – внутренняя точка области D. Точка , где лежит на поверхности S. Через точку M₀ можно провести бесконечное число плоскостей, так называемая связка плоскостей. Ограничимся рассмотрением плоскостей непараллельных оси Оz. Эти плоскости имеют уравнение

, (4.17)

здесь А и В произвольные постоянные числа.

Составим разность аппликат поверхности (4.16) z_пов. и плоскости z_пл. (4.17)

z_пов. – z_пл. = (4.18)

Если через обозначить расстояние от точки до точки Р(х,у), то в силу предположенной непрерывности , а потому из (4.18) находим, что .

Определение 1. Касательной плоскостью к поверхности z = f(x,y) в точке называется та из плоскостей (4.20), для которой разность z_пов. – z_пл. при есть бесконечно малая, порядка более высокого чем , т.е.

, причем (4.19)

Из этого определения, уравнение касательной плоскости находится единственным образом. Действительно, уравнению (4.19) с помощью (4.18) можно придать вид , и отсюда имеем

, (4.20)

здесь, и , а поэтому, из (4.20) следует, что функция f(x,y) дифференцируема в точке . Тогда, согласно теореме 2 (§2, п.2.1), числа A, B определяются равенствами . Значит уравнение касательной плоскости к поверхности S в точке следующее

. (4.21)

Итак, в предположении, что в точке к поверхности z = f(x,y) существует касательная плоскость, было доказано, что функция f(x,y) в точке Р₀ дифференцируема. После этого докажем обратное утверждение, а именно: если функция f(x,y) дифференцируема в точке , то к поверхности z = f(x,y) в точке существует касательная плоскость.

В самом деле, из дифференцируемости функции f(x,y) в точке

следует, что полное приращение этой функции в Р₀ представимо в виде

,

причем , или иначе

. (4.22)

Далее рассмотрим плоскость, заданную уравнением

. (4.23)

С помощью (4.23) равенство (4.22) можно записать в виде , а последнее равенство (так как ) означает, что плоскость, заданная уравнением (4.23) есть касательная плоскость к поверхности z = f(x,y) в точке .

Таким образом, из изложенного следует, что дифференцируемость функции f(x,y) в точке Р₀(х₀,у₀) равнозначна существованию касательной плоскости к поверхности, заданной уравнением z = f(x,y) в точке .

Теперь введем понятие нормали к поверхности.

Определение 2. Нормалью к поверхности z = f(x,y) в точке называется прямая перпендикулярная к касательной плоскости, заданной уравнением (4.23), и проходящая через точку касания .

Отсюда, используя условие перпендикулярности прямой и плоскости (книга 3, гл.4, §5), получаем уравнения нормали

.

Далее, находим формулы для вычисления направляющих косинусов нормали. Обозначая углы нормали с координатными осями Ох, Оу, Оz соответственно через имеем

.

В последних трех формулах берутся всюду либо верхние знаки, либо нижние знаки. Двойные знаки соответствуют двум направлениям для нормали.

Для выяснения геометрического значения полного дифференциала df(х₀,у₀) функции z = f(x,y) в точке Р₀(х₀,у₀) рассмотрим рис.30. Как было установлено, уравнение касательной плоскости Т в точке к поверхности , заданной уравнением z = f(x,y), имеет вид

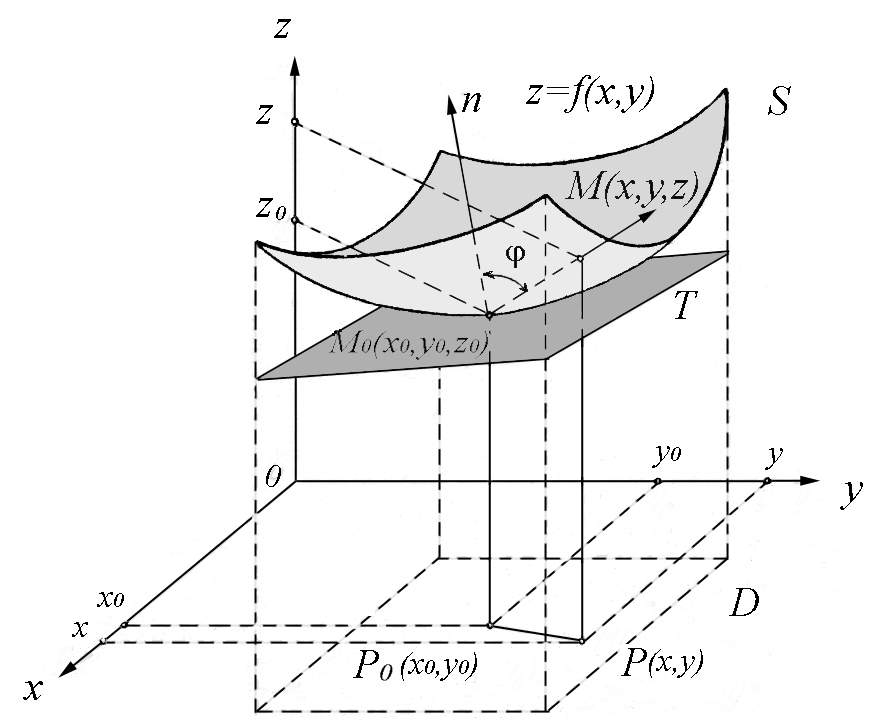
Рис. 30

Итак, получаем, что . Это равенство выражает геометрическое значение полного дифференциала функции z = f(x,y) в точке Р₀(х₀,у₀). Именно: полный дифференциал функции f(x,y) в точке Р₀(х₀,у₀) равен , т.е. приращению аппликаты касательной плоскости к поверхности S в точке , при переходе от точки Р₀(х₀,у₀) к точке Р(х,у) области определения D функции z = f(x,y).