§7. Частные производные высших порядков. Теорема о независимости результата от порядка дифференцирования

В начале, для определённости, речь пойдет о функциях двух независимых переменных

. (4.62)

Пусть для этой функции существуют частные производные

.

Эти частные производные будем называть частными производными первого порядка и они, вообще говоря, являются также функциями от x и y. Предполагая, что для этих функций также существуют частные производные, назовём их частными производными второго порядка от функции (4.62). Таким образом, частных производных второго порядка от функции имеется четыре, и они обозначаются, соответственно, следующим образом

Можно идти и дальше, вводя в рассмотрение восемь частных производных третьего порядка

.

Затем можно перейти к частным производным четвёртого порядка, число которых равно 16 = 2⁴. Вообще число частных производных порядка n равно 2ⁿ.

Пример 1. Найти все частные производные первого и второго порядка для функции . Прежде всего, находим две частные производные первого порядка

Далее, дифференцирование по x даёт

и затем, дифференцированием по y, находим .

Дифференцируя по x и затем по y, получаем

Заметим, что в этом примере всюду в плоскости xOy выполняется равенство

(4.63)

т.е., результат дифференцирования не зависит от того, в каком порядке оно выполнено: сначала по переменной x, а потом по y или же в обратном порядке.

Частные производные второго порядка в равенстве (4.63) будем называть смешанными частными производными второго порядка для функции .

Является ли равенство (4.63) случайным совпадением или же оно имеет место для любых функций?

Ниже приводится пример, показывающий, что не для всякой функции имеет место равенство (4.63).

Пример 2. Пусть функция задана следующим образом всюду в плоскости xOy, кроме точки O(0,0), а в самой точке O(0,0) полагаем . Докажем, что для этой функции . По определению имеем

Пользуясь этими предельными равенствами, сначала найдём .

.

Итак, получили

. (4.64)

Далее по определению имеем

Подставляя в последние два предельных равенства значения, полученные в (4.64), найдём

Поэтому для рассмотренной функции .

Однако нужно заметить, что в подавляющем числе случаев приходится иметь дело с такими функциями, для которых , как это следует из доказательства приводимой ниже теоремы. Даже в приведенном примере, в каждой точке плоскости xOy, за исключением единственной точки O(0,0), имеет место равенство смешанных частных производных второго порядка.

Теорема (о независимости результата от порядка дифференцирования). Пусть в точке P(x₀,y₀) и в некоторой её окрестности D для функции существуют частные производные

и пусть смешанные частные производные второго порядка и непрерывны в точке P(x₀,y₀). Тогда справедливо равенство

.

Для доказательства вводим в рассмотрение вспомогательное выражение

(4.65)

и считаем, что числа h и k достаточно малы по абсолютной величине, причём настолько, чтобы прямоугольник с вершинами в точках всеми своими точками лежал, внутри окрестности D рис.35.

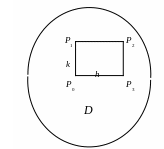
Рис. 35

Доказательство состоит из двух частей, в которых выражение Н преобразуется двумя различными способами. Далее приравнивая полученные значения для Н, и переходя в полученном равенстве к пределу, завершим доказательство.

1-ая часть доказательства. В правой части (4.65) сгруппируем первое слагаемое со вторым, а третье с четвёртым

. (4.66)

Введём вспомогательную функцию одного переменного

. (4.67)

Из (4.67) получаем

Теперь функция (4.66) принимает вид . Применяя в правой части теорему Лагранжа (гл.3, §4, п.4.2), все условия которой выполнены, получим

(4.68)

причём – некоторое число из интервала (0,1), 0 1.

Из (4.67) найдём производную функции : и полагая здесь , найдём .

Подставляя это в равенство (4.58), получим

. (4.69)

Далее введем вспомогательную функцию

(4.70)

и отсюда находим

Подставляя это в (4.69), получаем, что .

Преобразуем разность в правой части по теореме Лагранжа

, (4.71)

где . Из (4.70) найдём : и, подставляя здесь , имеем

. (4.72)

Из (4.71) и (4.72) находим, что

(4.73)

2-ая часть доказательства. На этот раз группируем в (4.65) вместе первое и третье слагаемое, а второе слагаемое с четвёртым

. (4.74)

Вводим вспомогательную функцию одного переменного у

. (4.75)

Отсюда: ; .

Теперь функция (4.74) приобретает вид и по теореме Лагранжа (гл.3, §4, п.4.2)

, где . (4.76)

Дифференцирование (4.75) даёт .

Положим здесь , тогда

и подставляя это в (4.76), находим

. (4.77)

Теперь введём вспомогательную функцию переменного х

. (4.78)

Отсюда

и потому (4.77) принимает вид .

Применение к разности, внутри квадратной скобки, теоремы Лагранжа приводит к равенству

, (4.79)

причём . Дифференцирование (4.78) дает

и, следовательно,

. (4.80)

Подставляя (4.80) в (4.79) получаем

. (4.81)

Теперь приравнивая значения (4.73) и (4.81) полученные для H приходим к равенству

и после сокращения на множитель , имеем

(4.82)

Далее воспользуемся предположенной непрерывностью смешанных частных производных второго порядка в точке P₀(x₀,y₀). Это означает справедливость предельных равенств

И применительно к данному случаю

, (4.83)

. (4.84)

Кроме того, из (4.82) имеем

(4.85)

Наконец из (4.83), (4.84) и (4.85) получаем .

Теорема доказана.

Доказанная теорема простыми рассуждениями может быть перенесена на функции любого числа независимых переменных.

В самом деле, рассмотрим функцию четырёх независимых переменных и пусть нужно доказать, что

. (4.86)

Но, при нахождении этих смешанных частных производных, функция дифференцируется по аргументам y и z и при этом нужно считать остальные два аргумента x и u постоянными x = x₀, u = u₀. Таким образом, речь идёт о доказательстве равенства (4.86) для функции двух независимых переменных y и z: . Поэтому здесь применима доказанная теорема.

Кроме того, установим также, что порядок дифференцирования не влияет на полученный результат и для частных производных порядка выше второго.

С этой целью докажем, что порядок двух смежных дифференцирований (например, третьего и четвёртого для функции ) можно менять местами, не изменяя результата дифференцирования, т.е.

. (4.87)

Введём обозначение . Тогда имеем

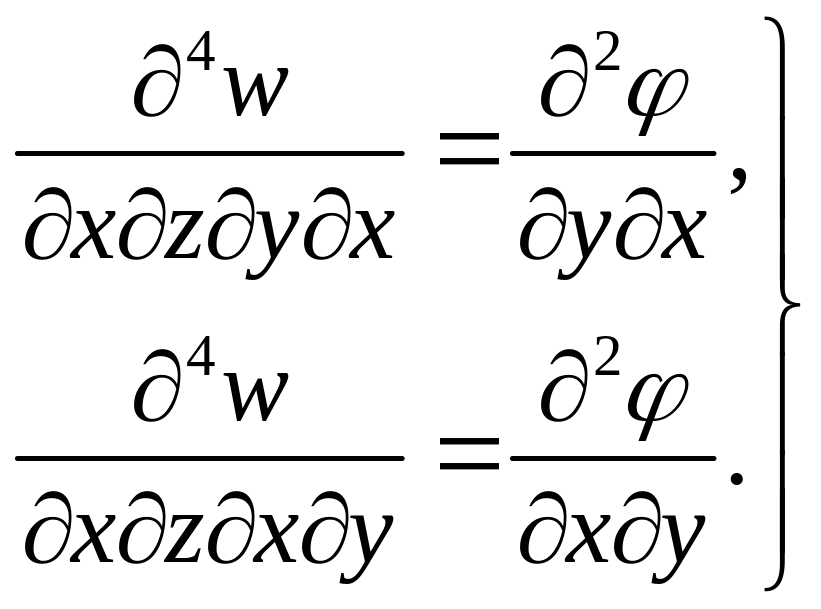(4.88)

Но при соблюдении условий указанной теоремы правые части (4.88) равны, а потому . Дифференцируя последнее равенство еще один раз по u, получим (4.87).

Поэтому, считая в дальнейшем все рассматриваемые функции такими, что для них результат дифференцирования не зависит от порядка дифференцирования, будем вместо писать или короче .

На основании изложенного можно составить следующую схему последовательных частных производных функции рис.36.

Рис. 36

Продолжая эту схему дальше и предполагая, что последовательные частные производные до некоторого порядка n существуют и непрерывны всюду в некоторой области плоскости xOy, получим всего (n + 1) частных производных порядка n для этой функции. В этом заключается упрощающая роль доказанной теоремы о независимости результата от порядка дифференцирования, следует напомнить, что первоначально (до доказательства упомянутой теоремы), число частных производных порядка n для функции было равно 2ⁿ.