2.2. Полный дифференциал функции многих переменных

Определение. Выражение линейным образом зависящие от Δx, Δy, является главной частью полного приращения (4.6) функции в точке P и называется полным дифференциалом функции f(x,y) в точке P(x,y) и обозначается через или dz

. (4.7)

Рассмотрим частный случай дифференцируемой функции всюду в плоскости хOу, когда . В этом случае приращение функции представлено в следующем виде

, (4.8)

а поэтому, полный дифференциал df, или что тоже, dx на основании (4.8) равен

, т.е. .

Точно также найдем, что .

Другими словами, для функции z = f(x,y) полное приращение функции Δz и полный дифференциал функции dz, вообще говоря, различны. Что касается независимых переменных, x, y, то справедливы точные равенства: т.е. дифференциал независимого переменного равен произвольному приращению этого аргумента. На основании двух последних равенств формуле (4.7) можно придать следующий окончательный вид

. (4.9)

Последнюю формулу пишут еще в такой форме

или .

Аналогичный вид имеет формула для полного дифференциала функции от n независимых переменных

или

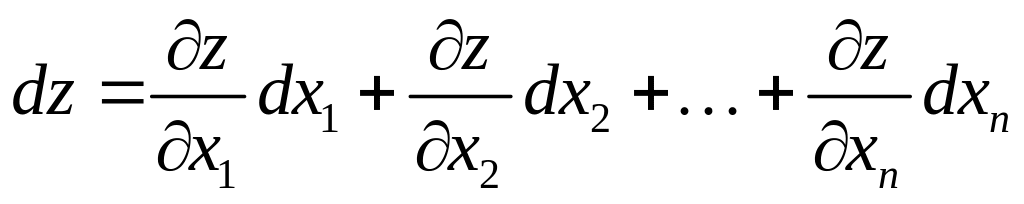, (4.10)

причем суть произвольные приращения соответствующих аргументов .

Из изложенного следует, что равенству (4.6) можно придать вид . Отсюда, при условии, что получаем приближенное равенство , которое широко используется в приближенных вычислениях.

Примеры: 1. Пусть нужно вычислить приближенно следующее выражение . Для этого введем в рассмотрение дифференцируемую функцию трех переменных . Рассмотрим полное приращение этой функции при переходе от точки к точке . Поскольку приращения переменных при переходе от точки к точке P достаточно малы , то, полное приращение функции, возможно заменить на полный дифференциал.

.

Так как , поэтому

Подставляя эти значения частных производных, а также значения , имеем .

2. В нефтеналивном судне один из его танков имеет форму прямоугольного параллелепипеда. При измерении ребер a,b,h этого параллелепипеда получены следующие результаты Найти абсолютную погрешность ρ и относительную погрешность δ при вычислении объема v такого танка.

Поскольку , а dx, dy и dz достаточно малы, то

Так как . Значит .

Подставляя эти значения, получим .

Отсюда и, кроме того

, здесь

Теперь сопоставим свойства дифференцируемых функций одной переменной f(x) и дифференцируемых функций многих переменных . Было доказано, что если функция f(x), дифференцируема в точке x = x₀, то для этой функции существует производная . Если функция дифференцируема в точке , то в этой точке существуют .

Далее из существования следует, что функция f(x) дифференцируема в точке x = x₀, однако, для функции многих переменных, существование не обеспечивает дифференцируемости непрерывной функции в точке . Другими словами: существование всех частных производных недостаточно для дифференцируемости непрерывной функции в точке .

В качестве примера рассмотрим функцию

Легко установить, что эта функция в точке O(0,0) непрерывна и имеет частные производные. Но, как это легко проверить, эта непрерывная функция, имеющая в точке O(0,0) обе частные производные по x и по y, не является дифференцируемой в точке O(0,0).

Из изложенного можно заключить, что свойства дифференцируемых функций одной переменной и многих переменных различны. В отличие от функции одной переменной существование всех частных производных уже недостаточно для дифференцируемости непрерывной функции в точке .