§ 8. Полные дифференциалы высших порядков для функции многих переменных

Пусть есть дифференцируемая функция от независимых переменных x и y, тогда полный дифференциал этой функции определяется равенством , будем называть его первым полным дифференциалом функции . Вторым полным дифференциалом (обозначается ) называется полный дифференциал от первого полного дифференциала .

Аналогично определяются полные дифференциалы третьего, четвёртого, и т.д. порядков

Исходя из этих определений, получим формулы для вычисления полных дифференциалов высших порядков.

Сначала рассмотрим второй полный дифференциал

.

Но, по предположению, x и y независимые переменные, а тогда dx и dy произвольные приращения x и y, которые, следовательно, ни от x ни от y не зависят, а поэтому при дифференцировании по x или по y должны рассматривать, как постоянные. Поэтому dx и dy можно выносить за знак дифференцирования. Значит

. (4.89)

Но

(4.90)

и аналогично

. (4.91)

Будем считать dx и dy в равенствах (4.89), (4.90) и (4.91) равными и тогда, с учетом теоремы о независимости результата от порядка дифференцирования, из этих формул получается, что

. (4.92)

Аналогично можно получить

. (4.93)

Замечаем, что формула (4.92) напоминает формулу квадрата суммы, а формула (4.83) формулу куба суммы двух слагаемых.

Желая установить формулу для вычисления полного дифференциала порядка n для , введём дифференциальный оператор

. (4.94)

Определим для дифференциального оператора (4.94) возвышение в натуральную степень n следующим образом: для возвышения в степень n дифференциального оператора (4.94) нужно применить формулу бинома Ньютона с последующей заменой «произведения» на оператор частной производной ,

«Умножение» оператора (4.94) на функцию сводится к тому, что свободные места в и в заполняются функцией . Поэтому формулы для первого, второго (4.92) и третьего (4.93) полных дифференциалов можно записать, используя, дифференциальный оператор (4.94), следующим образом:

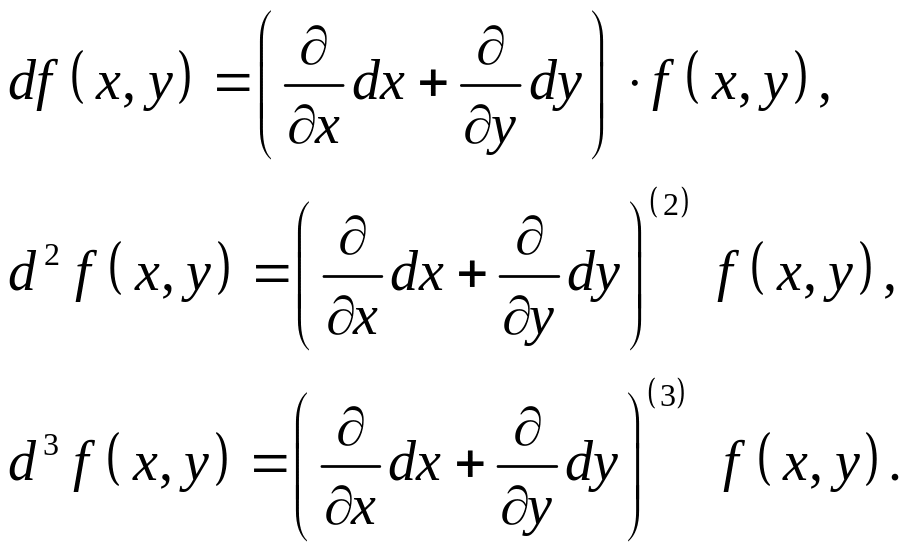
Докажем методом математической индукции, что при любом натуральном n справедлива формула

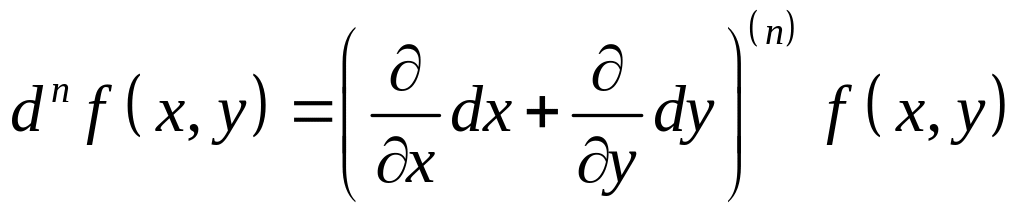. (4.95)

Для этого, предполагая, что формула (4.95) верна при некотором n, докажем её справедливость для .

В самом деле

.

Из предположенной справедливости формулы (4.95), имеем

.

Итак, доказано, что если верна формула

,

то тогда верна также формула

.

Но формула (4.95) верна для n = 3, а потому она верна при n = 4. Если же формула (4.95) верна для n = 4, то она же верна для n = 5 и так далее. Отсюда следует, что формула (4.95) верна для любого натурального n.

В случае функции от m независимых переменных справедлива аналогичная формула

.

После этого установим формулы для вычисления последовательных полных дифференциалов дифференцируемой функции в случае, когда аргументы x и y суть, дифференцируемые функции от других независимых переменных. Здесь первый полный дифференциал определяется по той же формуле, когда x и y являлись независимыми переменными

,

(инвариантность формы первого полного дифференциала), но dx и dy здесь уже не произвольные приращения x и y, а полные дифференциалы. Последовательные полные дифференциалы в этом случае определяются и обозначаются, как и прежде .

Исходя из этого, получим формулу для второго полного дифференциала, но только нужно помнить, что здесь нельзя выносить dx и dy как постоянные множители за знак дифференцирования. Пользуясь формулами полного дифференцирования (гл.3, §3, п.3.4), последовательно находим

Далее, имея в виду, что и применяя формулы (4.90) и (4.91), после упрощений имеем

. (4.96)

Отсюда, сравнивая (4.96) и (4.92), заключаем, что форма полного дифференциала не сохраняется, то есть инвариантность формы имеет место только для первого полного дифференциала. Это же замечание относится и к функциям трёх и большего числа аргументов.

В заключение сделаем одно замечание, которое будет использовано дальше.

Формула (4.95) была доказана в предположении, что аргументы x и y функции независимые переменные. Однако формула (4.95) остаётся верной и в том случае, когда x и y являются линейными функциями от независимых переменных

(4.97)

причём суть постоянные числа. Действительно, в этом случае

Отсюда заключаем, что dx и dy не зависят от , а потому

Из этих равенств и из (4.96) следует, что формула для вычисления будет такая же, как и в случае, когда x и y суть независимые переменные. Это же относится и к . Поэтому формула (4.95), для случая, когда имеет место (4.97), остаётся верной.