Глава 4 дифференциальное исчисление числовых функций многих действительных переменных
§1. Частные производные функции многих переменных
Для сокращения
записей сначала ограничимся рассмотрением
функции двух переменных z
= f(x,y),
которая задана в области D
плоскости хOу.
Пусть М(х,у)
есть внутренняя точка области D.
Это означает, что можно построить круг
достаточно малого радиуса, с центром в
точке М так,
чтобы все точки внутри этого круга были
бы точками области D.
Аргумент y
зафиксируем и зададим аргументу x
приращение
,
такое, чтобы точка
не выходила из области D.
При этом функция z
= f(x,y),
при переходе от точки М(х,у)
к точке
,
получит приращение, определяемое
равенством
. (4.1)
Такое приращение, как было уже сказано в гл.2, §4, п.4.1, называется частным приращением по аргументу x функции z = f(x,y) в точке М.
Аналогично
(4.2)
называется частным
приращением по аргументу y
функции f(x,y)
в точке М.
Если сразу оба аргумента x, y
функции f(x,y)
получают приращения, соответственно
,
то
(4.3)
называется полным приращением функции f(x,y) в точке М(х,у). Сначала обратимся к рассмотрению частных приращений (4.1) и (4.2) функции f(x,y), а затем, изучим полное приращение Δz (4.3).
Определения и обозначения частных производных
Составим отношение приращений:
.
Определение
1. Частной производной
функции z = f(x,y)
в точке М(х,у), по переменной
х, обозначается
,
называется предел отношения частного
приращения по x
к приращению аргумента Δх, вызвавшего
это приращение, когда приращение
аргумента стремится к нулю (
),
если этот предел существует, конечен и
не зависит от способа стремления Δх
к нулю, т.е.
.
Нужно обратить
особое внимание на способ обозначения
частной производной вместо прямого
d,
употребляется круглое
.
Для частной
производной употребляют и другие
обозначения. Вместо
пишут
,
аналогично определяется частная
производная по y.
Определение
2. Частной производной
функции z = f(x,y)
в точке М(х,у) по y,
обозначается
,
называется предел отношения частного
приращения по y
к приращению аргумента Δу, вызвавшего
это приращение, когда приращение
аргумента стремится к нулю (Δу
0),
если этот предел существует, конечен
и не зависит от способа стремления Δу
к нулю, т.е.
.
И в этом случае
для обозначения частной производной
употребляются и другие обозначения
.
Для нахождения частной производной функции z = f(x,y) по переменной x нужно иметь в виду, что аргумент y считается постоянным, следовательно, функция z = f(x,y) при этом превращается в функцию от одной переменной x и поэтому здесь могут применяться установленные прежде правила дифференцирования функций от одной переменной. Поэтому никаких новых правил для нахождения частных производных по x вводить не нужно. Такое же замечание нужно сделать и по поводу нахождения частной производной . В этом случае функция z = f(x,y) также превращается в функцию одного переменного y, а x рассматривается, как постоянная величина.
Совершенно
аналогично определяются и находятся
частные производные функции
с числом переменных более двух.
Пример 1. Найти
частные производные от функции
.
Для нахождения
считаем y постоянной.
Тогда
.
Далее, считая x
постоянной, находим
.
Напомним, что для
функции одной переменной y
= f(x)
производная
есть обычная дробь, числитель которой
есть дифференциал функции y = f(x),
а знаменатель есть произвольное
приращение независимой переменной x.
Наряду с этим следует подчеркнуть, что
для функции многих переменных, в
частности, для z =
f(x)
символы частных производных
нельзя рассматривать как дробь. Это
слитные символы, в которых нет числителя
и знаменателя. В этом можно убедиться
из рассмотрения следующего примера.
Пример 2. Рассмотрим уравнение Менделеева – Клайперона
(4.4)
Здесь
R –
универсальная газовая постоянная. В
уравнении (4.4) связаны между собой три
переменные величины Р (давление
газа), V (объем газа),
T (абсолютная температура
газа). Считая две переменные, из этих
трех, независимыми переменными, а тогда
третья переменная окажется функцией
от первых двух, получим три функции от
двух независимых переменных:
Для каждой из этих функций можно составить по две частных производных
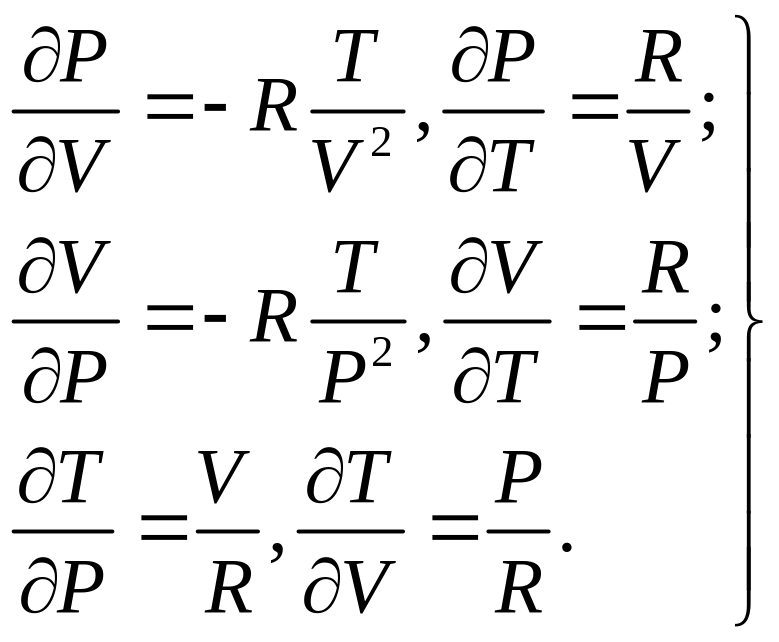(4.5)
Далее
составим произведение
.
С помощью (4.5) находим, что
Но если бы символ частной производной был бы дробью, то в результате сокращений произведение должно было бы равняться +1. Отсюда заключаем, что символ частной производной не дробь.