9.3 Види випадкових потоків

При розгляді випадкових процесів, які протікають в системах з дискретними станами і безперервним часом, часто доводиться стикатися з так званими «потоками подій».

Потоком подій називається послідовність однорідних подій, які слідують одне за одним у випадкові моменти часу.

Прикладами можуть бути:

• потік вимог на телефонній станції;

• потік вантажів, які поступають у складські приміщення;

• автомобілів, що надходять на АЗС, і т. ін.

При розгляді процесів, які протікають в системі з дискретними станами і безперервним часом, часто буває зручно уявити собі процес так, буцімто переходи системи із стану в стан проходять під дією якихось потоків подій (потік вимог, потік несправностей, потік заявок на обслуговування, потік відвідувачів і т. п.) Будемо зображувати потік подій послідовністю точок на осі часу 0t (рис.9.2).

Рис.9.2. Зображення потоку на часовій осі

Користуючись таким зображенням, слід пам'ятати, що положення кожної точки на осі 0t випадкове.

Потік подій зветься регулярним , якщо події слідують одне за одним через строго визначені проміжки часу. Такий потік порівняно рідко зустрічаються на практиці, але являє собою визначений інтерес як граничний випадок.

Частіше приходиться зустрічатися з потоками подій, для яких і моменти появи подій і проміжки часу між ними випадкові.

1. Потік подій зветься стаціонарним, якщо імовірність потрапляння того чи іншого числа подій на ділянку часу довжиною т (рис.9.2) залежить тільки від довжини ділянки і не залежить від того, де саме на осі 0t розташована ця ділянка.

2. Потік подій називається потоком без післядії, якщо для будь-яких ділянок часу, які не перетинаються, число подій, які потрапляють на один із них, не залежить від того, скільки подій потрапило на другу (або іншу, якщо розглядається більше двох ділянок).

3. Потік подій зветься ординарним, якщо імовірність потрапляння на елементарну ділянку двох або більше подій мала на стільки, що нею можна знехтувати в порівнянні з імовірністю потрапляння на неї однієї події.

Розглянемо більш детально ці три властивості потоків.

Стаціонарність потоку означає його однорідність в часі; імовірнісні характеристики такого потоку не повинні змінюватися залежно від часу. Зокрема, інтенсивність потоку подій — середнє число подій в одиницю часу — для стаціонарного потоку повинна залишатися постійною. Зрозуміло, це не означає, що фактична кількість подій, які з'являються в одиницю часу, постійна.

Потік може мати місцеві згущення і розрідження. Важливо, що для стаціонарного потоку ці згущення і розрідження не носять закономірного характеру, а середнє число подій, які потрапляють на одиничну ділянку часу, залишається постійним для усього періоду, який розглядається.

На практиці часто зустрічаються потоки подій, які (принаймні, на обмеженій ділянці часу) можуть розглядатися як стаціонарні. Наприклад, потік вимог, які потрапляють на телефонну станцію, скажемо, на інтервалі від 12 до 13 годин може вважатися стаціонарним. Той же потік на протязі цілої доби вже не буде стаціонарним (вночі інтенсивність потоку вимог набагато менша, ніж у день).

Відсутність післядії в потоці означає, що події, які утворюють потік, з'являються в послідовні моменти часу незалежно одна від одної. Наприклад, потік пасажирів, які входять на станцію метро, можна вважати потоком без післядії, тому що причини, які обумовлюють прихід окремого пасажира саме в даний момент, а не в іншій, як правило, не зв'язані з аналогічними причинами для інших пасажирів.

Ординарність потоку означає, що події в потік потрапляють поодинці, а не парами, трійками і т. п. Наприклад, потік клієнтів, які прямують до перукарні, практично можна вважати ординарним, чого не можна сказати про потік клієнтів, які прямують до ЗАГСу для реєстрації шлюбу. Потік атак винищувачів на бомбардувальник, який знаходиться над

ворожою територією, ординарний, якщо вони атакують ціль поодинці, і не ординарний, якщо вони атакують парами або трійками.

Якщо в неординарному потоці події відбуваються тільки парами, тільки трійками і т.д., то можна його розглядати як ординарний «потік пар», «потік трійок» і т. д.

Якщо потік подій не має післядії, ординарний, але не стаціонарний, він називається нестаціонарним пуассонівським потоком.

Розглянемо потік подій, який володіє всією трійкою властивостей: стаціонарний, без післядії, ординарний. Такий потік зветься простішим (або стаціонарним пуассонівським) потоком. Назва «простіший» пов'язана з тим, що математичний опис подій, пов'язаних з простішими потоками виявляється найбільш простою. Відмітимо також, що простіший потік відіграє серед інших потоків особливу роль.

Якщо потік подій не має післядії, ординарний, але не стаціонарний, він називається нестаціонарним пуассонівським потоком. В такому потоці інтенсивність λ, (середнє число подій в одиницю часу) залежить від часу

λ= λ(t), тоді, як для простішого потоку λ=const.

Пуассонівський потік подій (як стаціонарний, так і нестаціонарний) тісно пов'язаний з відомим розподілом Пуассона.

Окремим випадком пуассонівського закону розподілу, який описує ймовірність появи на інтервалі часу t певного числа подій, є експоненційний (показовий) закон розподілу, що описує ймовірність появи певного інтервалу часу між двома сусідніми подіями.

F(t) = 1-λe^-λt (t >0) (9.1)

Щільність розподілу часових інтервалів f(t) визначається формулою:

f(t) = λe^-λt (t >0) (9.2)

Величина X називається параметром експоненційного закону розподілу.

Числові характеристики цього закону розподілу: математичне сподівання т_t і дисперсія D_t визначаються формулами:

(9.3)

(9.4)

Середньоквадратичне відхилення випадкової величини від математичного очікування:

(9.5)

завжди дорівнює математичному очікуванню. Те ж саме стосується і їх оцінок, отриманих по результатах експерименту, що дозволяє зробити дуже важливий практичний висновок:

якщо експериментальні оцінки середньоквадратичного відхилення і математичного очікування рівні, то в якості моделі такого потоку можна прийняти розподіл Пуассона.

Недоліком експоненціального розподілу є те, що щільність експоненціального розподілу монотонно спадає, починаючи з максимального значення, визначеного для t=0, тобто імовірність появи інтервалу між двома фіксованими інтервалами зростає, коли ці значення наближаються до нуля. Але при дослідженні інтервалів часу між двома подіями часто зручно мати щільність розподілу, яка проходить через початок координат. Це відповідає тому, що імовірність коротких інтервалів дуже мала.

Найбільш придатною моделлю подібних потоків подій є потоки Ерланга, які часто називають потоками з післядією. Ці потоки утворюються в результаті «просіювання» простіших потоків.

Розглянемо на осі простіший потік подій (рис.9.3) і збережемо в ньому не всі точки, а тільки кожну другу, інші відкинемо (на рис.9.3), точки, які ми зберігаємо, показані жирними. В результаті такої операції «розрідження» або «просіювання» утворюється інший потік подій; який називається потоком Ерланга другого порядку.

Рис.9.3 Приклад формування потоку Ерланга 2-го порядку

Взагалі, потоком Ерланга к-го порядку називається потік, який утворюється, якщо в простішому потоці зберегти кожну к-ту точку, а решту відкинути.

Щоб визначити, як розподіляються проміжки часу між подіями в потоці Ерланга k-ro порядку, необхідно встановити закон розподілу. Закон розподілу інтервалу часу Т між сусідніми подіями в потоці Е_к називається законом Ерланга к-то порядку:

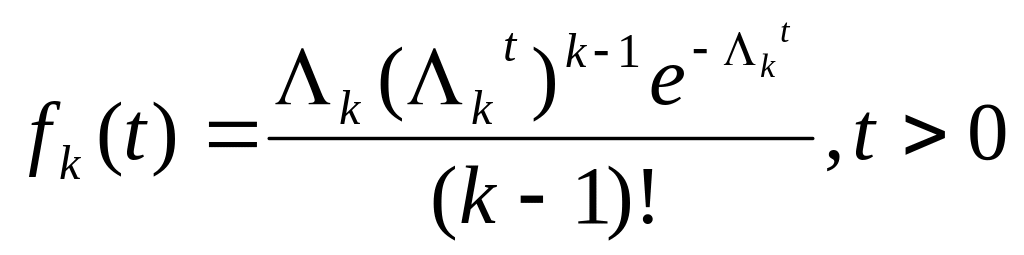(9.6)

де f_k^t - імовірність очікування тривалістю t для k-гo прибуття або здійснення

k-ї;

k, - параметр розподілу Ерланга;

k - ціле додатне число;

Λ_к - інтенсивність подій вхідного потоку.

Виразимо інтенсивність Λ_к та дисперсію самого потоку Ерланга через інтенсивність породжуючого його вхідного потоку λ:

Λ_к= λ/ k; λ= k Λ_к (9.7)

При цьому середній інтервал часу між подіями та його середньо-квадратичне відхилення визначаються як

(9.8)

З цих формул слідує, що при необмеженому зростанні параметра к середньоквадратичне відхилення прямує до нуля, тобто розкид статистичних характеристик зменшується. Це означає, що при зростанні параметра к потік Ерланга заданої інтенсивності необмежено наближається до регулярного потоку з постійним інтервалом між подіями:

Т=1/Λ_к – const. (9.9)

Ця властивість потоків Ерланга зручна при практичному використанні: задаючись різними к, можна отримувати потоки, яким притаманна різна післядія - від цілковитої відсутності післядії (k=1) до жорсткого функціонального зв'язку між моментами появи подій .Тому можна вважати, що параметр к вказує на міру післядії та ступінь регулярності потоку.

9.4 Методи генерування потоків подій з різними законами розподілу ймовірностей

Практично усі випадкові потоки подій мають у своїй основі потік з рівномірним законом розподілу ймовірностей, котрий далі трансформується в потік з будь-яким законом розподілу. Тому розглянемо більш детально властивості і алгоритм формування саме цього потоку.

Перш за все, це є потік рівномірно розподілених випадкових чисел, значення яких належать відрізку [0, 1]. Опишемо властивості цих чисел.

Нагадаємо, що випадкова величина X має рівномірний розподіл на відрізку [0, 1]. Щільність розподілу ймовірностей має вигляд:

(9.10)

Математичне очікування та дисперсія такого розподілу: т_х=\/2; σ²_x=1/12. В ЕОМ генерування потоку випадкових чисел, що мають такий закон розподілу, здійснюється за допомогою оператора " rnd ". Практично при цьому застосовується досить проста процедура:

u_i+1 = FRAC(k · и.), де k = 8t ± З, t - непарне ціле число.

Часто застосовують значення t=5, k=37 або k=39. При цьому необхідно задавати довільне початкове значення u₀ < 0. Отримана таким чином послідовність чисел у достатньо великій кількості буде розподілена рівномірно на інтервалі [0,1]. Отримана послідовність не є чисто випадковою, тому що застосовує детермінований алгоритм генерації. Це означає, що числа будуть випадковими лише протягом одної послідовності. При повторі вони, строго кажучи, будуть повторюватись, якщо не змінити початкове значення u₀. Щоб запобігти цьому явищу, застосовують оператор " randomize " з метою випадкового варіювання значення u₀.

Для генерування випадкової рівномірно розподіленої послідовності чисел в будь якому інтервалі [а,b] застосовують трансформацію генерованої послідовності и_i (і = ) за допомогою формули:

Випадкові послідовності, що є розподілені по нормальному (гаусовському) закону розподілу, отримуються звичайно трансформацією послідовності з рівномірним розподілом за допомогою формул:

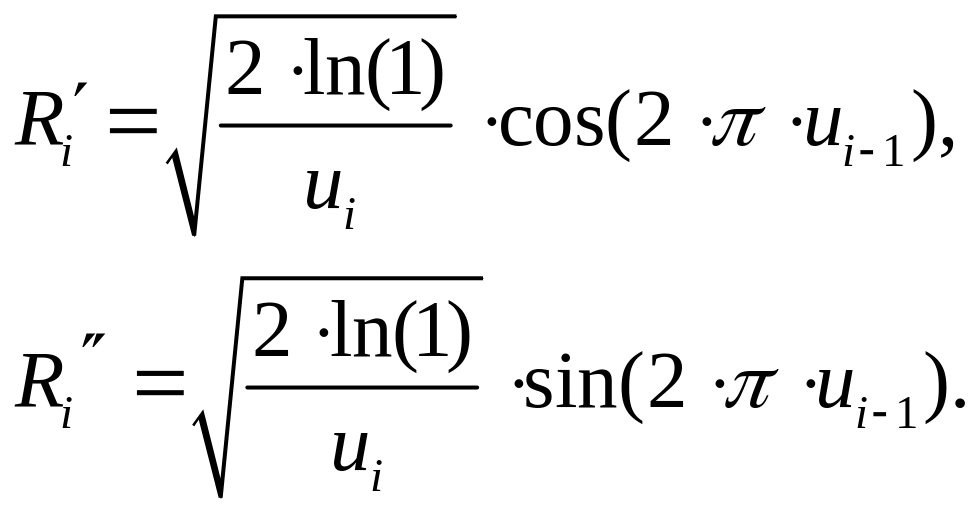
При цьому генерується послідовність нормально розподілених чисел, що мають математичне очікування m_R=0 і дисперсію σ²_R=l. При інших значеннях m_R і σ²_R цю послідовність трансформують наступним чином:

При необхідності генерувати потік Пуассона з експоненційним законом розподілу часових інтервалів між подіями у потоці, послідовність з рівномірним розподілом трансформується за допомогою наступної формули:

(9.11)

Величина (1-u_i) також має рівномірний розподіл на відрізку [0,1]. Тому вираз для x_i можна написати простіше:

(9.12)

При моделюванні потоків Ерланга випадкову величину хі можна розіграти по формулі, запропонованій у книзі проф. Соболя І.М[8]:

(9.13)

де и₁ ≤ u₂ ≤... ≤ и_к - випадкові числа отримані оператором "rnd" в діапазоні [0, 1]), при умові їх розташування в порядку зростання. Саме необхідність впорядкування потоку чисел и_i робить цей метод дещо складним. Тому в [5] запропоновано новий метод трансформації випадкових чисел, отриманих оператором "rnd" в діапазоні [0, 1]), а саме за допомогою формули:

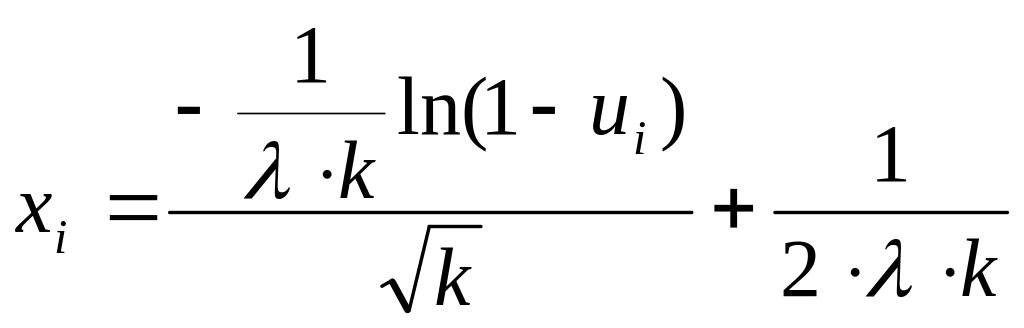(9.14)

Зауважимо, що при застосуванні цього методу немає необхідності ранжирувати початковий потік, що значно спрощує задачу генерації.

В таблиці 9.1 наведені чисельні характеристики потоків, отриманих за допомогою вказаних методів. Там же наведені результати формування потоку шляхом простого просіювання.

Таблиця 9.1 Порівняльна характеристика різних методів генерування потоків Ерланга (А=1)

Методи моделювання	К
	1		2		3		4		5
	тх	σх	тх	σх	тх	σх	тх	σх	тх	σх
теоретичні значення	1,000	1,000	1,000	0,707	1,000	0,577	1,000	0,500	1,000	0,447
Просте просіювання	0,992	0,939	0,947	0,922	0,967	0,843	0,924	0,897	1,050	0,997
Метод (II)	1,456	0,958	1,224	0,717	1,035	0,535	1,033	0,528	0,892	0,375
Метод (І)	0,992_	0,939	0,975	0,638	0,992	0,545	0,975	0,445	0,969	0,433

Порівняння результатів свідчить про те, що просте просіювання не дає задовільного результату. Обидва інші методи майже рівнозначні, за винятком к=1. Далі, при розробці програми імітаційного моделювання систем масового обслуговування з непуоссонівськими потоками заявок буде передбачена можливість застосування як одного, так і другого методу генерування потоків Ерланга. Але при к=1 доцільніше користуватись стандартною процедурою генерування потоку Пуассона.