Численные методы математической физики

Лабораторная работа №1

1. Метод сеток для задачи дирихле

1.1. Основы метода сеток

Основой метода сеток (метода конечных разностей) является идея замены дифференциальных операторов конечно-разностными отношениями (операторами). Пусть в плоскости хОу имеется некоторая область G с границей Г, (рис.1).

Построим на плоско­сти два семейства параллельных прямых:

х = х₀ + ih (i = 0, ± 1, ±2,...), у=у₀ +kl (k = 0, ± 1, ±2, ...)

у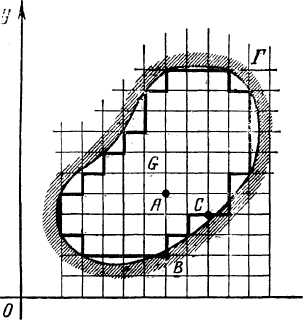

х

Рис.1

Точки пересечения этих прямых назовем узлами. Два узла называ­ются соседними, если они удалены друг от друга в направлении оси Ох или Оу на расстояние, равное шагу сетки h или l соответствен­но. Выделим узлы, принадле­жащие области G+Г, а также некоторые узлы, не принадлежащие этой об­ласти, но расположенные на расстоянии, меньшем чем шаг, от границы Г. Те узлы, у которых все четыре соседних узла принадлежат выделенному множе­ству узлов, называются внутренними (узел А, рис. 1). Оставшиеся из выде­ленных узлов называются граничными (узлы В, С, рис. 1).

Значения искомой функции u = u(х, у) в узлах сетки будем обозначать через

u_ik = u(x₀ + ih, y₀ + kl). В каждом внутреннем узле (x₀ + ih, y₀ + kl) заменим

частные производные разностными отношениями:

, ;

в граничных точках получаются менее точные формулы:

, .

Частные производные второго порядка заменяются конечно-разностными отношениями следующим образом:

, .

1.2. Разностные отношения для задачи Дирихле.

Рассмотрим краевую задачу Дирихле для уравнения Пуассона

(1)

Необходимо найти функцию u=u(x,y), удовлетворяющую внутри некоторой области G уравнению (1), а на границе Г – условию

(2)

где - заданная непрерывная функция.

Согласно вышеизложенному будем иметь

, (3)

где

Уравнения (3) вместе со значениями u_ik в граничных узлах образуют систему линейных алгебраических уравнений относительно значений функции u(x,y) в узлах (x_i,y_k). Наиболее простой вид эта система имеет для прямоугольной области и для l = h. В этом случае уравнения (3) записываются следующим образом:

u_i+1,k + u_i-1,k + u_i,r+1 +u_i,k-1 - 4u_ik =h²f_ik , (4)

а значения в граничных узлах в точности равны значениям граничной функции. При

f(x,y) = 0 уравнение (1) называется уравнением Лапласа и соответствующие конечно-разностные уравнения имеют вид

(5)

П

(i+1,k+1)

ри составлении уравнений (4) и (5) была использована схема узлов, изображенная на рис.2. Здесь и в дальнейшем на рисунках указаны только индексы узла, например узел

( x_i , y_k) обозначается через (i , k). Иногда бывает удобнее использовать схему узлов, указанную на рис. 3.

(i-1,k+1)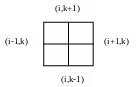

(i,k)

(i,k)

(i-1,k-1)

(i+1,k-1)

Рис.2 Рис.3

В этом случае уравнению Лапласа соответствуют следующие конечно-разностные уравнения:

, (6)

а для уравнения Пуассона будем иметь

.

Погрешность замены дифференциального уравнения разностным, т.е. остаточный член R_ik для уравнения Лапласа, оценивается неравенством

где .

Погрешность приближенного решения, полученного разностным методом, складывается из трех погрешностей:

1. Погрешности замены дифференциального уравнения разностным;

2. Погрешности аппроксимации краевых условий;

3. Погрешности, получаемой в результате того, что система разностных уравнений решается приближенным методом.

ПРИМЕР.

Рассмотрим задачу о стационарном распределении тепла в плоской квадратной изолированной пластинке со стороной 1, если на границе пластинки поддерживается постоянная температура.

Известно, что функция u(x,y) , дающая распределение температуры, является решением уравнения Лапласа

при краевых условиях, изображенных на рис.4.

РЕШЕНИЕ.

Строим сетку с шагом h=1/4. Получим девять внутренних узлов (рис.4). Записываем в этих узлах конечно-разностные уравнения.

В силу симметрии граничных условий имеем

u₁₁ = u₃₁, u₁₂ = u₃₂, u₁₃ =u₃₃. (7)

Э

5000

10000

0

10000

10000

5000

0

0

0

0

0

0

0

0

0

0

0

(1.3)

(2,3)

3,3)

(1,2)

(2,2)

(3,2)

(1,1)

(2,1)

(3,1)

то сокращает число неизвестных значений функции u во внутренних узлах до шести. Таким образом, в узлах (3,1), (3,2), (3,3)

Рис.4

конечно-разностные уравнения писать не нужно. В остальных шести внутренних узлах (1,1), (2,1), (1,2), (2,2), (1,3), (2,3) получаем соответственно шесть уравнений:

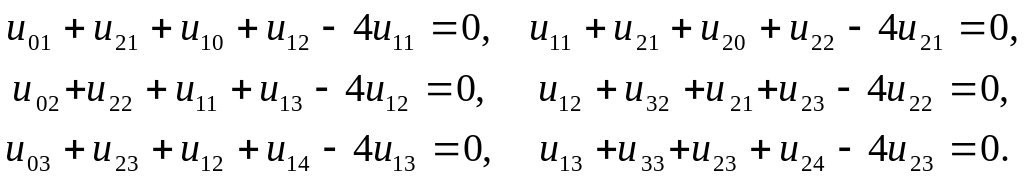(8)

В эти уравнения входят еще 12 значений функции в граничных точках. Эти значения мы берем из краевых условий.

(9)

Заметим, что в остальных узлах краевые условия не используются.

Окончательно, учитывая условия (7), (9), получаем систему

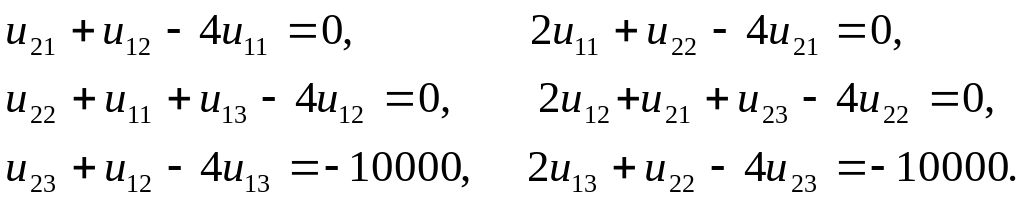
Решив эту систему методом Гаусса, получим

u₁₁ = 714, u₂₁ = 982, u₁₂ = 1875, u₂₂ =2500, u₁₃ = 4286, u₂₃ = 5268.