20

Лабораторная работа 1 Определение величины иллюзии Мюллера—Лайера методом минимальных изменений

Цель работы: отработать метод минимальных изменений применительно к измерению разностного порога. Оценить величину иллюзии Мюллера—Лайера.

Теория

Дифференциальный (разностный) порог, наряду с абсолютным порогом, является пороговой мерой чувствительности сенсорной системы.

Дифференциальный (разностный) порог (DL) определяется как наименьшая разница между двумя стимулами, превышение которой приводит к восприятию их различия. Испытуемый воспринимает два стимула одинаковыми, если различие между ними меньше дифференциального порога.

Для измерения порогов чувствительности – специальных значений психологической переменной – предназначены методы нольмерного шкалирования. С их помощью можно определить положение единственной точки на шкале в психологическом пространстве, поэтому их часто также называют методами локализации точки на психологической шкале. Из числа этих методов чаще всего для определения абсолютных и дифференциальных порогов используют следующие: метод минимальных изменений, метод средней ошибки, или метод подравнивания, установки, метод постоянных раздражителей, или метод констант. В данной работе для вычисления дифференциального порога применяется метод минимальных изменений, состоящий в следующем.

Испытуемому одновременно предъявляются два стимула – эталонный и переменный. Задача испытуемого заключается в том, чтобы в каждой пробе сравнивать переменный стимул со стандартным и давать одну из трех реакций: «меньше», «равно», «больше». Испытуемый должен дать ответ на каждый шаг изменения стимула в ряду. Эти ответы экспериментатор заносит в протокол.

Переменные стимулы предъявляются восходящими и нисходящими рядами, начиная с нисходящего. В нисходящем ряду предъявление переменных стимулов начинается со стимула отчетливо большего эталона, а заканчивается на стимуле, отчетливо меньшем эталона. В восходящем ряду, наоборот – от меньшего к большему. Восходящие и нисходящие ряды должны предъявляться парами для уравновешивания их числа путем чередования. Это условие необходимо для сбалансирования ошибок привыкания или ожидания, которые нередко появляются при измерении порогов. Ошибка привыкания заключается в том, что испытуемый продолжает повторять тот же ответ, что и на предыдущем шаге, хотя порог уже пройден и стимул в нисходящем ряду уже не вызывает ощущения. Ошибка ожидания или предвосхищения – ошибка противоположного толка.

Кроме того, для повышения точности и надежности данных, полученных в ходе эксперимента, используется еще один экспериментальный прием – изменение длины стимульных рядов от пары к паре за счет смещения в случайном порядке начального и конечного значения стимулов в ряду. Эта предосторожность служит для предупреждения возможности повторения испытуемым своих ответных реакций на основе простого отсчета от начала и конца ряда определенного количества шагов изменения стимула.

В каждом стимульном ряду определяются две пороговые точки: верхний (L_h) и нижний (L_l) дифференциальные пороги. За порог принимается значение стимула, соответствующее середине межстимульного интервала, в котором впервые произошла смена категории ответа по отношению к ответу «равно»: от «больше» к «равно» и от «равно» к «меньше» в нисходящем ряду, а в восходящем ряду – от ответа «меньше» к ответу «равно» и от ответа «равно» к ответу «больше».

Значения верхнего (L_h) и нижнего (L_l) дифференциальных порогов усредняются по всем рядам (как нисходящим, так и восходящим):

, ,

где n – число предъявленных испытуемому рядов стимулов.

Верхний и нижний дифференциальные пороги ограничивают интервал неопределенности (IU) – зону стимульного ряда, в которой преобладают ответы равенства. Иначе говоря, интервал неопределенности – это та зона стимулов, которая сверху ограничена стимулом, в среднем едва заметно отличающимся от эталонного, как больший, а снизу – стимулом, в среднем едва заметно отличающимся от эталонного, как меньший. Таким образом, он равен разности между верхним и нижним дифференциальными порогами:

IU = L_h – L_l.

Середина интервала неопределенности называется точкой субъективного равенства:

PSE = .

Такое название она получила потому, что стимул, находящийся в средней точке интервала неопределенности, является субъективным эквивалентом эталонного стимула S_st и оценивается как равный ему. Однако, вследствие ошибок измерения интервал неопределенности, как правило, не симметричен, поэтому точка субъективного равенства PSE не совпадает со значением эталона S_st, и степень их несовпадения характеризуется константной ошибкой CE = PSE – S_st.

Константная ошибка CE характеризует величину и направление смещения зоны субъективного равенства относительно объективного равенства: если CE > 0, то эталон переоценивается, если CE < 0, то эталон недооценивается.

Так как интервал неопределенности – это та зона стимулов, которая сверху ограничена стимулом, в среднем едва заметно отличающимся от эталонного, как больший, а снизу – стимулом, в среднем едва заметно отличающимся от эталонного, как меньший, то он содержит две различительные ступени или два едва заметных различия. Поэтому интервал неопределенности IU равен двум дифференциальным порогам DL, отсюда:

DL = = .

Естественно, что нельзя вычислить параметр DL, но можно определить его экспериментальную оценку:

,

где – среднее арифметическое, – ширина доверительного интервала. Среднее арифметическое дифференциального порога можно рассчитать, вспомнив свойства мат. ожидания:

,

то есть .

Доверительный интервал рассчитывается по стандартной формуле:

,

где инструментальная составляющая равна половине шага, а случайная составляющая определяется как обычно:

.

Для расчета среднего квадратического отклонения сложной функции s(DL) рассмотрим свойства дисперсии:

1. D(CX) = C² D(X)

2. D(X –Y) = D(X) +D(Y)

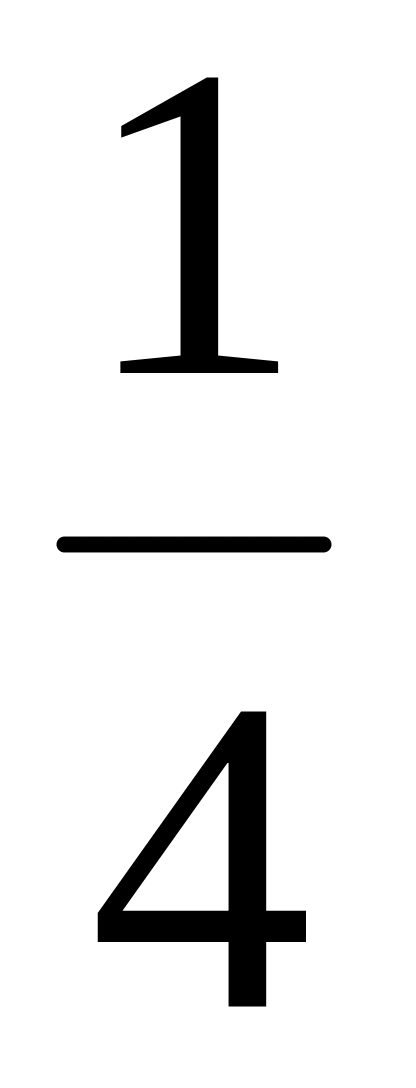3. D(DL) = D( ) = [D(L_h) + D(L_l)].

Следовательно, .

В данной лабораторной работе вычисляется дифференциальный порог зрительного анализатора. Отметим, что именно с этим анализатором связано большое количество иллюзий. Одна из наиболее известных – иллюзия Мюллера–Лайера, которая состоит в том, что из стрел одинаковой длины короче выглядит стрела с наконечниками наружу. В рамках данной работы можно проверить это, то есть определить наличие иллюзии, выяснить ее характер, оценить величину. Таким образом, целью данной работы наряду с определением разностного порога является определение величины и характера иллюзии Мюллера–Лайера.