1.0.0. Решение уравнений Максвелла для непоглощающего диэлектрика
Найдем
общее решение уравнения (1.22) для вектора
,
в предположении, что
зависит только от одной из координат,
например,
.
Это означает, что
имеет постоянное значение в точках
плоскости, перпендикулярной оси
.
Решение будем искать в виде
,
где
- некоторая функция, зависящая от
переменных
.
При этих допущениях уравнение для примет вид:
,
Уравнение
имеет решение отличное от нуля только
при
.
Это возможно для
,
,
Общее решение может быть представлено в виде
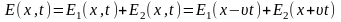(1.23)
Зависимост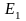и
и
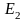от
в моменты времени
и
показаны на рис. 1.2.
Рис.
1.2. Изменение функции
и
в различные моменты времени
и
.
Рассмотрим
физический смысл решения (1.23). Для функции
значения аргумента в точке
в момент времени
совпадают со значениями аргумента
функции в точке
при
,
поэтому график функции во время
получается из графика для
смещением всех точек кривой
в направлении положительных значений
на
.
В процессе движения значения
в каждой точке волны и форма волны не
изменяются. Исходя из этого, можно
сделать заключение, что функция
действительно описывает гармоническую
волну. Аналогично
описывает поперечную волну, движущейся
со скоростью
в направлении отрицательных значений
оси
(см. рис. 1.2). Без существенного ограничения
общности можно ограничиться рассмотрением
лишь одной из волн, например
.
В одномерном случае значение для фиксированных и является постоянным на плоскости, перпендикулярной оси . Такие волны называют плоскими. Плоская волна называется монохроматической, если поле волны является гармонической (синусоидальной) функцией времени. В этом случае
(1.24)
описывает
монохроматическую волну, которая
распространяется в направлении
положительных значений
.
Постоянная
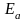называется амплитудой волны,
- ее частотой.
Аргумент
гармонической функции (1.24) называется
фазой. Введя понятие длины волны
,
запишем (1.24) в виде
(1.25)
- период,
- фазовая скорость,
- волновое число,
численно равно числу волн, укладывающихся
на длине окружности единичного радиуса.
Чтобы
не зависеть от системы координат, удобно
записать (1.25) в векторной форме. Пусть
вектор
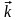равен по модулю волновому числу и
направлен вдоль оси
(рис. 1.3). Этот вектор называется волновым.
Рис. 1.3. К записи плоской волны в векторной форме.
Учитывая рис. 1.3, вместо (1.25) можно записать
(1.26)
Принимая
во внимание, что при произвольном
направлении волнового вектора, для
произвольной точки пространства,
характеризуемой радиус-вектором
,
справедливо представление
,
то это выражение описывает плоскую
монохроматическую волну, распространяющуюся
в трехмерном пространстве в направлении
вектора
.
Оно не зависит от системы координат.
Аналогичное выражение для плоской
монохроматической волны можно записать
с использованием синуса
(1.27)
Любое
комплексное число
,
используя формулу Эйлера
,
можно записать в экспоненциальной форме
;
,
Представим выражения (1.26), (1.27) в комплексной форме
,
(1.28)
где
- амплитуда вектора
.
Независимость
от координат означает, что распространение
плоских монохроматических волн в
непоглощающем диэлектрике не связано
с изменением их интенсивности.
Величина в (1.28) является комплексной, поэтому не может описывать реальный физический процесс, который характеризуется вещественной величиной в виде (1.26) или (1.27). По этой причине, для перехода к физическим величинам необходимо взять действительную или мнимую части полученного выражения. Действительными физическими параметрами, которые нас интересуют, являются проекции вращающегося вектора на горизонтальную и вертикальную оси.