0.2.1. Метод возмущений
Одним из наиболее универсальных методов анализа нелинейных систем является метод возмущений. Основная идея этого метода состоит в том, что сначала описывают движение системы в линейном приближении, а затем рассматривают нелинейный эффект как малую поправку.
Предположим, что амплитуда колебаний осциллятора настолько мала, что в любой момент времени нелинейный член в уравнении (0.19) много меньше линейных слагаемых, в частности,
,
(0.20)
или
.
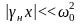(0.21)
Тогда решение уравнения (0.19) можно представить в виде
,
(0.22)
где
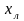— решение линейного уравнения
,
(0.23)
а
— нелинейная поправка, малая по сравнению
с
:
.
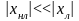(0.24)
0.2.2.0. Линейное приближение
Запишем световое поле в виде плоской монохроматической волны
(0.25)
и подставим (0.25) в (0.23). Решение уравнения (0.23) ищем в виде
(0.26)
Подставив (0.26) в (0.23), находим
(0.27)
или
,
(0.28)
где введена величина
,
(0.29)
которая называется линейной поляризуемостью атома. Тем самым задача в линейном приближении решена.
0.2.3.1. Расчет нелинейной поправки
Подставив (0.22) в (0.19), получим уравнение
.
(0.30)
Поскольку есть решение уравнения (0.23), то часть членов в уравнении (0.30) сокращается и оно приобретает вид
.
(0.31)
Среди оставшихся членов выделим члены низшего порядка малости, а остальными пренебрежем. Учитывая (0.24), получим
,
(0.32)
а принимая во внимание (0.21)
.
(0.33)
В итоге получаем уравнение
.
(0.34)
Таким образом, мы провели линеаризацию исходного нелинейного уравнения (0.19) по малому параметру .
Уравнение
(0.34) представляет собой линейное уравнение
вынужденных колебаний, в котором роль
вынуждающей силы играет член
,
определяемый решением уравнения движения
электрона в линейном приближении. Найдем
решение уравнения (0.34). Согласно (0.26)
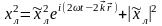(0.35)
Таким
образом, вынуждающая сила содержит
постоянную составляющую и переменную
компоненту, осциллирующую на частоте
второй гармоники
.
В силу линейности уравнения (0.34), такую
же структуру будет иметь и величина
.
Поэтому ищем решение в виде
.
(0.36)
Подставив (0.35), (0.36) в (0.34), получим уравнение
(0.37)
Приравнивая коэффициенты при экспонентах, а также постоянные слагаемые, находим
,
.
(0.38)
Таким образом, нелинейная поправка вычислена.
Итак, приближенное решение уравнения (0.19) получено. Теперь нетрудно вычислить поляризацию среды. Подставив (0.22), (0.26), (0.36) в (0.8), (0.9), получим
,
(0.39)
где
(0.40)
— линейная
поляризация
(0.41)
— нелинейная
поляризация, а величины
,
,
,
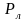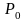определяются формулами
,
,
(0.42)
или, в силу (0.28), (0.38)
(0.43)
где
— линейная поляризуемость атома,
определяемая формулой (0.29).
Формулы (0.39)-(0.43) показывают, что поляризация рассматриваемой нелинейной среды содержит три спектральные компоненты: компоненту на частоте возбуждающей световой волны (линейная поляризация), компоненту на частоте и постоянную составляющую (рис. 0.3). Компонента поляризации на частоте ответственна за генерацию второй оптической гармоники.
Рис. 0.3. Спектр возбуждающей световой волны (а) и спектр поляризации (б) в квадратично-нелинейной среде