
- •Часть I
- •Оглавление
- •Предисловие
- •Введение
- •1. Основные положения классической электродинамики.
- •1.0. Уравнения Максвелла.
- •1.0.0. Решение уравнений Максвелла для непоглощающего диэлектрика
- •1.0.1. Свойства электромагнитной волны
- •1.0.1.0. Энергия электромагнитной волны
- •1.0.1.1. Давление света
- •1.0.1.2. Закон Снеллиуса
- •1.1. Оптические характеристики проводящих сред
- •1.1.1. Оптические постоянные вещества и его микрохарактеристики
- •1.1.1.0. Временная дисперсия
- •1.1.1.1. Временная дисперсия и частота излучения
- •1.1.1.2. Пространственная дисперсия
- •1.1.2. Дисперсионные соотношения
- •0. Поглощение излучения металлами и их оптические свойства
- •0.0. Распространение электромагнитных волн в проводящих средах. Основные уравнения оптики металлов
- •0.0.0. Скин-эффект и его свойства
- •0.1. Оптические свойства металлов
- •0. Поглощение света и передача энергии в полупроводниках
- •0.0. Оптические процессы в поглощающих полупроводниках
- •0.1. Рекомбинация и захват электронов и дырок в полупроводниках
- •0.2. Процессы передачи энергии в поглощающих полупроводниках
- •0.2.1. Особенности собственного поглощения
- •0.2.2. Внутризонное поглощение
- •0.3. Кинетика фотовозбуждения полупроводников лазерным излучением
- •0.4. Насыщение межзонного поглощения
- •0. Влияние интенсивности излучения на оптические свойства вещества. Нелинейная оптика
- •0.0. Основные эффекты нелинейной оптики
- •0.1. Материальное уравнение нелинейной среды
- •0.2. Нелинейный осциллятор
- •0.2.1. Метод возмущений
- •0.2.2.0. Линейное приближение
- •0.2.3.1. Расчет нелинейной поправки
- •0.3. Осциллятор с кубичной нелинейностью. Зависимость частоты колебаний от амплитуды
- •0.4. Самовоздействие света в нелинейной среде. Самофокусировка
- •0.5. Явление самоиндуцируемой прозрачности
- •0.6. Неоднородный ансамбль нелинейных осцилляторов. Световое эхо
- •0. Изменение поглощательной способности прозрачных диэлектриков в процессе лазерного облучения
- •0.0. Физические представления о механизмах изменения поглощения в идеальных диэлектриках
- •0.0.0. Фотоионизация газа
- •0.0.1. Многофотонная ионизация.
- •0.0.2. Лавинная ударная ионизация
- •0.0.3. Изменение поглощения в идеально чистых прозрачных твердых телах
- •0.0.4. Роль вынужденного рассеяния Мандельштама Бриллюэна
- •0.1. Оптические свойства реальных оптических материалов и покрытий
- •0.1.0. Механизмы инициирования объемного поглощения в первоначально прозрачной среде
- •0. Поверхностные электромагнитные волны оптического диапазона
- •0.0. Основные свойства пэв, структура и распределение полей, условия существования, дисперсионное соотношение
- •0.1. Поверхностные плазмон-поляритоны на границе металла с диэлектриком
- •0.2. Методы возбуждения пэв
- •0.2.0. Призменный метод возбуждения пэв
- •0.2.1. Возбуждение пэв на решетке
- •0.3. Цилиндрические пэв
- •0. Оптическая «левитация»
- •0.0. Оптическая «левитация» малых прозрачных частиц
- •0.1. Элементы теории оптической «левитации»
- •0.1.0. Геометрия отражения и преломления.
- •0.1.1. Энергетика отражения и преломления
- •0.1.2. Формулы Френеля.
- •0.1.3. Силы светового давления
- •0.1.4. Световое давление вдоль пучка
- •0.1.5. Световое давление поперек пучка
- •0.2. Численные оценки
- •Вопросы для самопроверки
- •Рекомендуемая литература
- •Кафедра лазерных технологий и экологического приборостроения
- •История кафедры лт и эп делится на
- •4 Разных периода:
- •1) Лазерное формирование многофункциональных зондов (мз) для зондовой микроскопии с целью создания универсальных зондовых микроскопов.
- •3) Наноструктурирование тонких металлических и полупроводниковых слоев.
- •4) Управление микрогеометрией, наношероховатостью и физико–химичекими свойствами поверхности материалов
- •2. Лаборатория лазерной очистки и реставрации произведений культуры и искусства (пкин) организована совместно с фирмой ооо «Мобильные лазерные системы».
- •Евгений Борисович Яковлев, Галина Дмитриевна Шандыбина Взаимодействие лазерного излучения с веществом (силовая оптика).
0.1.1. Энергетика отражения и преломления
Рассмотрим
луч света, падающий в точку
(рис. 0.2). Обозначим интенсивности
падающего, отраженного и преломленного
лучей соответственно через
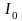 ,
,
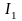 ,
,
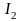 .
По закону сохранения энергии
.
По закону сохранения энергии
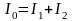 (0.2)
(0.2)
Введем коэффициенты отражения и пропускания Т света по интенсивности в точке :
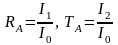 .
(0.3)
.
(0.3)
В силу (0.2) сумма коэффициентов отражения и пропускания равна единице
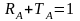
Аналогично для точки , расположенной на задней границе шара, можно написать
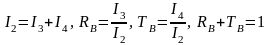
Таким
образом, для полного описания энергетики
отражения и преломления света на границах
шара достаточно вычислить два параметра:
коэффициенты отражения
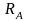 и
и
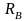 .
Эту задачу можно решить с помощью формул
Френеля.
.
Эту задачу можно решить с помощью формул
Френеля.
0.1.2. Формулы Френеля.
Как
известно из теории Френеля, коэффициенты
отражения и преломления света на границе
раздела двух сред зависят от состояния
поляризации падающей световой волны.
Поэтому предположим, что лазерный пучок,
падающий на частицу, линейно поляризован
(как это обычно имеет место в экспериментах).
Не ограничивая общности рассмотрения,
будем считать далее, что вектор
напряженности электрического поля в
падающей волне
,
лежащий в плоскости фронта волны
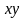 ,
направлен вдоль оси
,
как показано на рис. 0.4.
,
направлен вдоль оси
,
как показано на рис. 0.4.
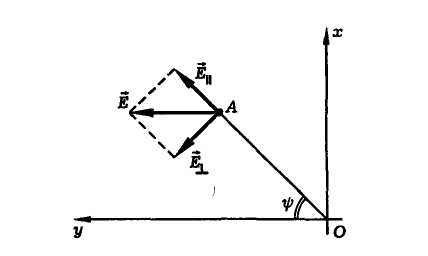
Рис.
0.4. Разложение вектора напряженности
электрического поля падающей волны
на компоненты параллельную (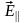 )
и перпендикулярную (
)
и перпендикулярную (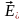 )
плоскости падения луча в точку
.
Плоскость рисунка совпадает с плоскостью
фронта падающей волны
)
плоскости падения луча в точку
.
Плоскость рисунка совпадает с плоскостью
фронта падающей волны
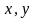 .
Плоскость падения луча в точку
изображена прямой линией
.
Плоскость падения луча в точку
изображена прямой линией
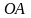 (
=const)
(
=const)
Разложим
вектор
поля падающей волны на компоненты
параллельную (
)
и перпендикулярную (
)
плоскости падения луча в точку
![]() .
Тогда
.
Тогда
![]() =
=![]() +
+![]() ,
(0.4)
,
(0.4)
где модули соответствующих векторов связаны соотношениями (см. рис. 0.4)
![]() .
(0.5)
.
(0.5)
Коэффициенты отражения света по интенсивности для компонент поля падающей волны параллельной и перпендикулярной плоскости падения определяются формулами Френеля:
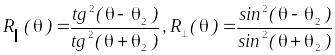 ,
(0.6)
,
(0.6)
где
![]() — угол падения луча в точку
,
— угол падения луча в точку
,
![]() — угол преломления. Согласно закону
Снеллиуса (0.0), величина угла
определяется формулой
— угол преломления. Согласно закону
Снеллиуса (0.0), величина угла
определяется формулой
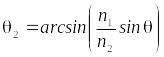 ,
(0.7)
,
(0.7)
в
которой
![]() и
и
![]() — показатели преломления среды,
окружающей частицу, и материала самой
частицы.
— показатели преломления среды,
окружающей частицу, и материала самой
частицы.
Из выражений (0.4)–(0.7) следует, что полный коэффициент отражения света по интенсивности в точке дается формулой
![]() .
(0.8)
.
(0.8)
Отражение луча на задней границе шара (в точке В) описывается теми же формулами (0.6), (0.8), в которых углы и следует теперь поменять местами (рис. 0.2). При этом получим
![]()
и, соответственно,
![]() .
(0.9)
.
(0.9)
Таким образом, вся энергетика отражения и преломления света на границах шара описывается одной единственной независимой величиной
![]() ,
,
которая определяется формулой
![]() .
(0.10)
.
(0.10)
Здесь
и
![]() — сферические координаты точки
падения луча на поверхность шара, а
функции
— сферические координаты точки
падения луча на поверхность шара, а
функции
![]() и
и
![]() определяются формулами (0.6), (0.7). Вид этих
функций, а значит и вид коэффициента
отражения
определяются формулами (0.6), (0.7). Вид этих
функций, а значит и вид коэффициента
отражения
![]() ,
зависят только от относительного
показателя преломления
,
зависят только от относительного
показателя преломления
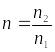 .
.
Что же касается коэффициентов пропускания света, то согласно формуле (0.9), они (как и коэффициенты отражения) одинаковы на обеих границах шара, т. е.
![]()
причем
коэффициент пропускания
![]() однозначно определяется значением
коэффициента отражения
:
однозначно определяется значением
коэффициента отражения
:
![]() .
(0.11)
.
(0.11)
В дальнейшем для расчета сил светового давления нам понадобятся средние величины вида
![]() .
(0.12)
.
(0.12)
Подставляя (0.10) в (0.12) и выполняя интегрирование, получаем
![]() ,
(0.13)
,
(0.13)
где
функции
![]() и
и
![]() определяются формулами (0.6). Формулы (0.11)
и (0.13) позволяют вычислить и другие
средние, а именно,
определяются формулами (0.6). Формулы (0.11)
и (0.13) позволяют вычислить и другие
средние, а именно,
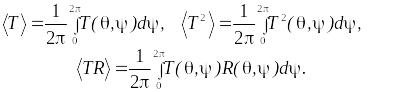 (0.14)
(0.14)
В силу линейности операции интегрирования по и линейности связи (0.11) величин и получаем
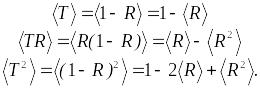 (0.15)
(0.15)
Перейдем к расчету сил светового давления.
