Общая постановка задачи идентификации параметров дискретных моделей
В большинстве случаев, когда говорят об идентификации параметров моделей речь идет об оперативной идентификации параметров в процессе функционирования системы управления. Часто речь идет об адаптивных системах управления с контуром оперативной идентификации параметров управления.
Постановка задачи.
Пусть объект описывается в виде разностного уравнения вида:
y(k)+a1y(k-1)+a2y(k-2)+...+amy(k-m)=
=b1U(k-d-1)+b2U(k-d-2)+...+bmU(k-d-m)
d–запаздывание на целое число тактов
При идентификации объекта к нему подходят таким образом:
Такая модель называется полной моделью дискретного объекта управления. В общем случае порядок числителя и знаменателя канала помехи равен “m”, т.е. соответствует порядку основного канала, но не больше.
При решении задач по полной модели должны учитывать ai, bi, ci, di.
В такой постановке решение задачи идентификации моделей в принципе возможно, но представляет собой сложную вычислительную задачу и требует большое количество времени для её решения.
На практике часто в качестве модели дискретного объекта используют усеченную модель вида:
Учитывая тот факт, что параметры фильтра
помехи зависят от вида знаменателя его
ПФ и только тесно связанные с параметрами
ПФ реального объекта основного канала,
то логично в качестве фильтра помехи
взять звено с ПФ вида
.
Такое упрощение позволяет упростить
методику решения задач идентификации
параметров модели, уменьшить размерность
задачи.
Таким образом решение задач оперативной идентификации дискретной модели требует рекуррентных подходов или методов для определения интересующих нас коэффициентов. Сущность рекуррентной методики заключается в том, что текущие оценки параметров модели мы должны получать на основании текущих измерений выхода и входа реальной модели и их значений на предыдущем такте.
Рекуррентный метод наименьших квадратов для идентификации моделей дискретных объектов (рмнк)
Предположим, что мы имеем модель идеального дискретного объекта, которая, которая представлена в виде разностного уравнения n-го порядка. А также имеем оценки параметров модели до (к-1) такта наблюдения, мы можем измерить значение векторов yk, тогда разностное уравнение мы можем записать так:
e(k) – невязка уравнения (обусловленная неточностью параметров nизмерения).
Исходя из таких представлений о разностном уравнении и наличии в нем невязки мы можем трактовать выходное значение y(k) как предсказанное в момент (k-1)
– вектор данных (измерений)
θ – вектор оцениваемых параметров
Выражение для ошибки уравнения:
Если известна предыстория наблюдения, то разностное уравнение для объекта можем записать из (N+1) уравнений:
в интервалеk=1,2,...,m+d+N,
можно представить в векторно-матричной форме:
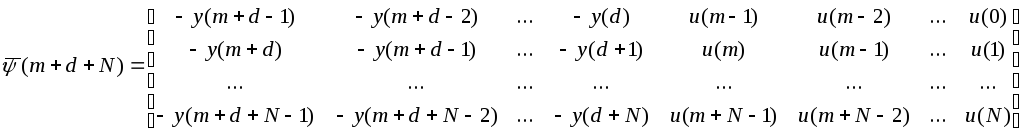
Минимум невязки
находится из условия:
Мы получим систему, содержащую 2m
уравнений, решая которую получим значение
компонент вектора
.
Это классическое МНК (и не является рекуррентным)
Для получения рекуррентного варианта
алгоритма МНК достаточно записав
выражения для оценок
и
,
вычесть второе из первого:
.
( Новая оценка=старая оценка+вектор коррекц × [ Новое измерение – предсказанное значение новое измерение] )
Вектор коррекции γ определяется:
Исходными данными являются: