
- •2.Раскрытие неопределённости по правилу Лопиталя.
- •3.Формула Тейлора.
- •4.Формула Маклорена.
- •Остаточный член
- •5.Монотонность и экстремумы функции.
- •6.Промежутки выпуклости.7.Точка перегиба.
- •8.Асимптоты графика функции.
- •9.Анализ свойств функции, и её построение.
- •10.Неопределённый интеграл.
- •11. Свойства неопределённого интеграла.
- •12.Методы интегрирования (метод разложения).
- •18.Дифференциальные биномы.
- •Выразимость в элементарных функциях
- •[Править]Связь с бета-функцией и гипергеометрической функцией
- •19.Интегрирование тригонометрических функций.
- •20.Определённый интеграл.
- •22. Формула Ньютона-Лейбница.
- •23.Формула замены переменной (интегрирование подстановкой).
- •24. Интегрирование по частям определённого интеграла.
- •25.Несобственные интегралы. Интеграл от неограниченной функции.
- •27. Интеграл с бесконечными пределами.
- •28.Приложения определенного интеграла.
- •Вычисление площади фигуры, ограниченной параметрически заданной кривой.
- •31.Площадь криволинейного сектора и сегмента.
- •33.Объем произвольного тела.
- •34.Объем тела вращения.
- •35.Площадь поверхности вращения
- •36. Механические приложения определённого интеграла (работа сил, статические моменты, центр тяжести).
- •38. Предел функции нескольких переменных. Непрерывность.
- •40. Полный дифференциал.
- •41.Производные сложных функций.
- •42. Производная по направлению. Градиент
- •43.Частные производные и дифференциалы высших порядков.
- •44. Дифференцирование неявных функции.
- •45.Замена переменных в дифференциальных выражениях
- •46. Формула Тейлора для функции нескольких переменных.
- •47. Экстремумы функции нескольких переменных.
- •48.Абсолютный экстремум
- •49. Условный экстремум. Метод множителей Лагранжа.
- •50. Геометрические приложения (Касательная прямая и нормальная плоскость к пространственной кривой, к поверхности заданной явно, к поверхности заданной неявно).
- •51. Двойные интегралы.
- •52.Свойства двойных интегралов.
- •53.Теорема о среднем значении. Сведение двойных интегралов к повторным.
- •54. Замена переменных в двойных интегралах.
- •55. Тройные интегралы.56.Сведение к повторным.57.Замена переменных
- •58. Интегрирование непрерывной функции по неограниченной области.
- •66. Формула Грина и её применение.
- •69. Формула Стокса. Формула Остроградского.
28.Приложения определенного интеграла.
1. Вычисление площади криволинейной трапеции.
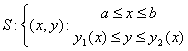
![]()

П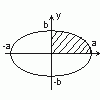 ример. Вычислить площадь ограниченную
эллипсом
ример. Вычислить площадь ограниченную
эллипсом ![]()
Ввиду очевидной симметрии эллипса относительно осей координат, достаточно вычислить четвёртую часть площади, расположенную в правом верхнем квадранте.
Из
уравнения эллипса находим y как
функцию от x: y(x)=b
Тогда площадь эллипса вычисляем по формуле:
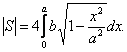 Сделав
замену x=asint,
Сделав
замену x=asint, ![]() получим
интеграл:
получим
интеграл: 
Площадь «сложной» фигуры
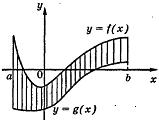
Под «сложной»
фигурой будем понимать часть плоскости,
ограниченную непрерывными на отрезке
[а; b] кривыми у = f(x) и у = g(x) (f(x) ![]() g(x),
x
g(x),
x ![]() [а;
b]) и прямыми х = а, х = b.
Площадь «сложной»
фигуры находится по формуле:
[а;
b]) и прямыми х = а, х = b.
Площадь «сложной»
фигуры находится по формуле:
![]()
Вычисление площади фигуры, ограниченной параметрически заданной кривой.
При
выяснении геометрического
смысла определенного интеграла,
мы получили формулу для нахождения
площади криволинейной трапеции,
ограниченной осью Ох,
прямыми x
= a, x = b и
непрерывной неотрицательной
(неположительной) функцией y
= f(x).
В некоторых случаях функцию, которая
ограничивает фигуру, удобно задать в
параметрическом виде, то есть, представить
функциональную зависимость через
параметр t.
В этой статье мы разберемся, как находить
площадь фигуры в случае параметрического
задания ограничивающей кривой.
После
краткого обзора теории и вывода формулы,
мы подробно рассмотрим решение характерных
примеров на нахождение площади.
Пусть
границами криволинейной трапеции
являются прямые x
= a, x = b,
ось абсцисс и параметрически заданная
кривая 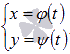 ,
причем функции
,
причем функции ![]() и
и ![]() непрерывны
на интервале
непрерывны
на интервале ![]() ,
монотонно
возрастает на нем и
,
монотонно
возрастает на нем и ![]() .
Тогда
площадь криволинейной трапеции находится
по формуле
.
Тогда
площадь криволинейной трапеции находится
по формуле 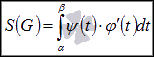 .
Эта
формула получается из формулы площади
криволинейной трапеции
.
Эта
формула получается из формулы площади
криволинейной трапеции 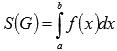 подстановкой
:
подстановкой
:
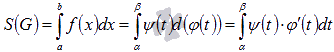 Если
функция
является
монотонно убывающей на интервале
Если
функция
является
монотонно убывающей на интервале ![]() ,
то формула примет вид
,
то формула примет вид 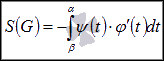 .
Если
функция
не
является основной элементарной, то для
выяснения ее возрастания или убывания
может потребоваться теория из
раздела возрастание
и убывание функции на интервале.
.
Если
функция
не
является основной элементарной, то для
выяснения ее возрастания или убывания
может потребоваться теория из
раздела возрастание
и убывание функции на интервале.
31.Площадь криволинейного сектора и сегмента.
Пусть кривая L задана в полярной системе координат уравнением r = r(θ), α ≤ θ ≤ β (см. Рис. 3), причем функция r(θ) непрерывна и неотрицательна на сегменте [α, β]. Плоскую фигуру, ограниченную кривой L и двумя лучами, составляющими с полярной осью углы α и β, будем называть криволинейным сектором.
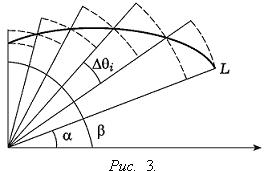
Докажем следующее утверждение. Криволинейный сектор представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле
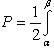
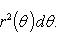 (2)
(2)
Доказательство.
Рассмотрим разбиение T сегмента
[α, β]
точками α = θ0 < θ1 <
... < θn = β и
для каждого частичного сегмента
[θi-1, θi]
построим круговые секторы, радиусы
которых равны минимальному ri и
максимальному Ri значениям r(θ)
на сегменте [θi-1, θi].
В результате получим две веерообразные
фигуры, первая из которых содержится в
криволинейном секторе, а вторая содержит
криволинейный сектор (эти веерообразные
фигуры изображены на Рис. 3).
Площади ![]() и
и ![]() указанных
веерообразных фигур равны
соответственно
указанных
веерообразных фигур равны
соответственно ![]()
![]() и
и ![]()
![]() .
Отметим, что первая из этих сумм является
нижней суммой s для
функции
.
Отметим, что первая из этих сумм является
нижней суммой s для
функции ![]() для
указанного разбиения T сегмента
[α, β],
а вторая сумма является верхней
суммой S для
этой же функции и этого же разбиения.
Так как функция
интегрируема
на сегменте [α, β],
то разность
для
указанного разбиения T сегмента
[α, β],
а вторая сумма является верхней
суммой S для
этой же функции и этого же разбиения.
Так как функция
интегрируема
на сегменте [α, β],
то разность ![]()
![]() может
быть как угодно малой. Например, для
любого фиксированного ε >
0 эта разность может быть сделана
меньше ε/2.
Впишем теперь во внутреннюю веерообразную
фигуру многоугольник Qi с
площадью Si,
для которого
может
быть как угодно малой. Например, для
любого фиксированного ε >
0 эта разность может быть сделана
меньше ε/2.
Впишем теперь во внутреннюю веерообразную
фигуру многоугольник Qi с
площадью Si,
для которого ![]()
![]() ,
и опишем вокруг внешней веерообразной
фигуры многоугольник Qd площадью Sd,
для которого
,
и опишем вокруг внешней веерообразной
фигуры многоугольник Qd площадью Sd,
для которого ![]()
![]() *.
Очевидно, первый из этих многоугольников
вписан в криволинейный сектор, а второй
описан вокруг него. Так как справедливы
неравенства
*.
Очевидно, первый из этих многоугольников
вписан в криволинейный сектор, а второй
описан вокруг него. Так как справедливы
неравенства
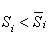
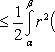
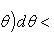
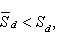 (3)
(3)
то, очевидно, Sd - Si < ε. В силу произвольности ε, отсюда вытекает квадрируемость криволинейного сектора. Из неравенств (3) вытекает справедливость формулы (2).
Площадь
криволинейного сектора и сегмента
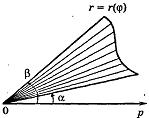 Площадь
сектора, ограниченного непрерывной
кривой r = r(
Площадь
сектора, ограниченного непрерывной
кривой r = r(![]() )
и лучами
=
)
и лучами
= ![]() ;
=
;
= ![]() (
<
),
равна
(
<
),
равна
![]()
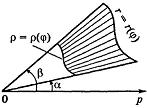 Площадь
сегмента, ограниченного непрерывными
кривыми r = r(
)
и р = р(
)
и лучами
=
;
=
(
<
),
равна
Площадь
сегмента, ограниченного непрерывными
кривыми r = r(
)
и р = р(
)
и лучами
=
;
=
(
<
),
равна
![]()
