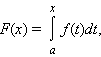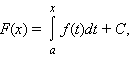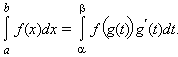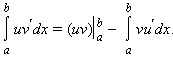- •2.Раскрытие неопределённости по правилу Лопиталя.
- •3.Формула Тейлора.
- •4.Формула Маклорена.
- •Остаточный член
- •5.Монотонность и экстремумы функции.
- •6.Промежутки выпуклости.7.Точка перегиба.
- •8.Асимптоты графика функции.
- •9.Анализ свойств функции, и её построение.
- •10.Неопределённый интеграл.
- •11. Свойства неопределённого интеграла.
- •12.Методы интегрирования (метод разложения).
- •18.Дифференциальные биномы.
- •Выразимость в элементарных функциях
- •[Править]Связь с бета-функцией и гипергеометрической функцией
- •19.Интегрирование тригонометрических функций.
- •20.Определённый интеграл.
- •22. Формула Ньютона-Лейбница.
- •23.Формула замены переменной (интегрирование подстановкой).
- •24. Интегрирование по частям определённого интеграла.
- •25.Несобственные интегралы. Интеграл от неограниченной функции.
- •27. Интеграл с бесконечными пределами.
- •28.Приложения определенного интеграла.
- •Вычисление площади фигуры, ограниченной параметрически заданной кривой.
- •31.Площадь криволинейного сектора и сегмента.
- •33.Объем произвольного тела.
- •34.Объем тела вращения.
- •35.Площадь поверхности вращения
- •36. Механические приложения определённого интеграла (работа сил, статические моменты, центр тяжести).
- •38. Предел функции нескольких переменных. Непрерывность.
- •40. Полный дифференциал.
- •41.Производные сложных функций.
- •42. Производная по направлению. Градиент
- •43.Частные производные и дифференциалы высших порядков.
- •44. Дифференцирование неявных функции.
- •45.Замена переменных в дифференциальных выражениях
- •46. Формула Тейлора для функции нескольких переменных.
- •47. Экстремумы функции нескольких переменных.
- •48.Абсолютный экстремум
- •49. Условный экстремум. Метод множителей Лагранжа.
- •50. Геометрические приложения (Касательная прямая и нормальная плоскость к пространственной кривой, к поверхности заданной явно, к поверхности заданной неявно).
- •51. Двойные интегралы.
- •52.Свойства двойных интегралов.
- •53.Теорема о среднем значении. Сведение двойных интегралов к повторным.
- •54. Замена переменных в двойных интегралах.
- •55. Тройные интегралы.56.Сведение к повторным.57.Замена переменных
- •58. Интегрирование непрерывной функции по неограниченной области.
- •66. Формула Грина и её применение.
- •69. Формула Стокса. Формула Остроградского.
18.Дифференциальные биномы.
В математическом анализе дифференциальным биномом или биномиальным дифференциалом называется интегралвида
![]()
где m, n, p, a, b — действительные числа.
Выразимость в элементарных функциях
Дифференциальный бином выражается в элементарных функциях только в трёх случаях:
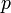 —
целое
число;
—
целое
число;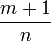 —
целое
число;
—
целое
число;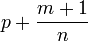 —
целое
число.
—
целое
число.
[Править]Связь с бета-функцией и гипергеометрической функцией
Дифференциальный бином выражается через неполную бета-функцию:
![]()
где ![]() ,
а также через гипергеометрическую
функцию:
,
а также через гипергеометрическую
функцию:
![]()
19.Интегрирование тригонометрических функций.
1°. Интегралы вида
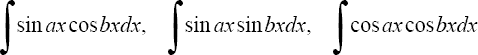
находятся с помощью тригонометрических формул
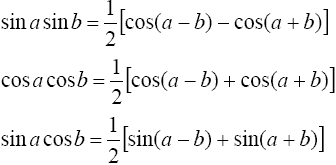
2°. Интегралы вида
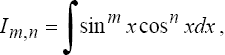
где m и n - четные числа находятся с помощью формул понижения степени
![]()
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
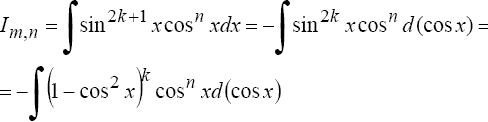
Примеры.
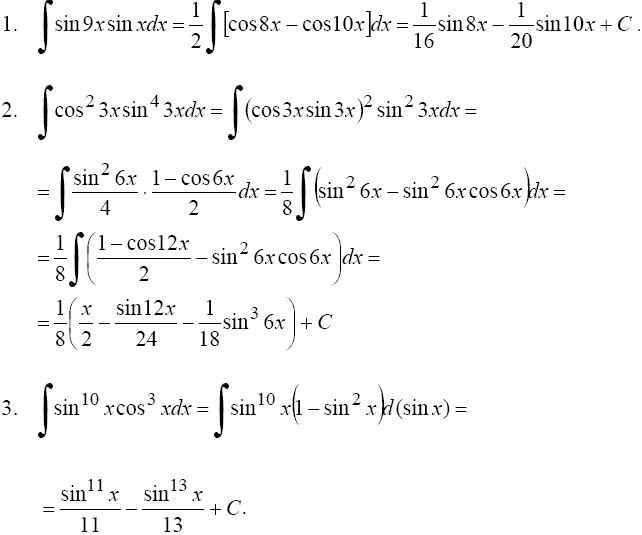 3°.
Если m = -,
n = - -
целые отрицательные числа одинаковой
четности, то
3°.
Если m = -,
n = - -
целые отрицательные числа одинаковой
четности, то

В частности, к этому случаю сводятся интегралы
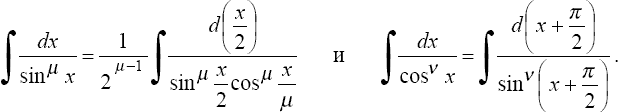
Примеры. 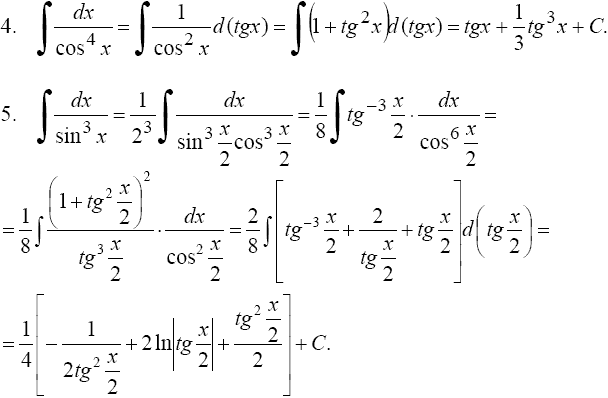 4°.
Интегралы вида
4°.
Интегралы вида
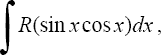
где
R - рациональная функция от sinx и cosx,
приводятся к интегралам от рациональных
функций новой переменной с помощью
подстановки
![]() при
этом
при
этом
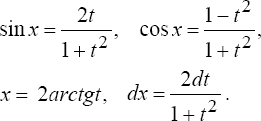 Если
R{-sin x, cosx) = R(sinx, cosx), то целесообразно
применить подстановку tgx = t. при этом
Если
R{-sin x, cosx) = R(sinx, cosx), то целесообразно
применить подстановку tgx = t. при этом
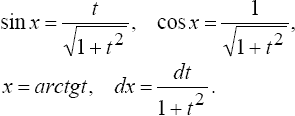
Примеры.
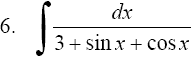 Здесь
подынтегральная функция является
рациональной функцией от sinx и cosx.
Применяем подстановку
Здесь
подынтегральная функция является
рациональной функцией от sinx и cosx.
Применяем подстановку
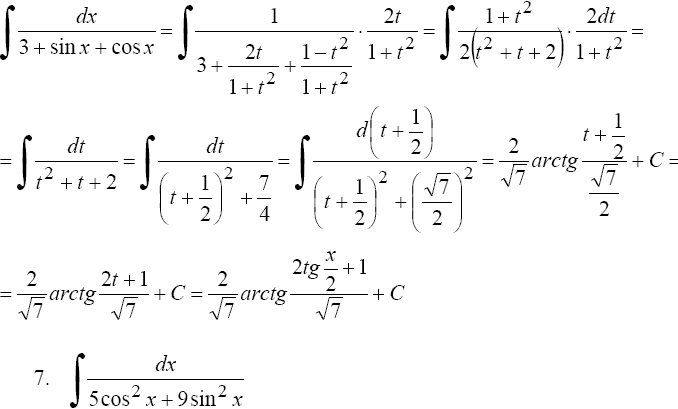 Подынтегральная
функция не меняется от замены sinx на
(-sinx), cosx на (-cosx), то есть R(-sinx,cosx) =
R(sinx,cosx) . Применим подстановку tgx = t:
Подынтегральная
функция не меняется от замены sinx на
(-sinx), cosx на (-cosx), то есть R(-sinx,cosx) =
R(sinx,cosx) . Применим подстановку tgx = t:
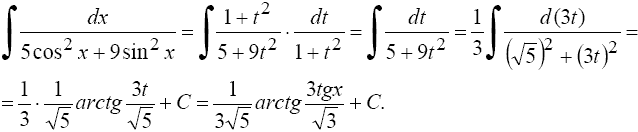
20.Определённый интеграл.
Определение и свойства.
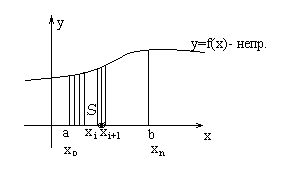
S – область – криволинейная трапеция.
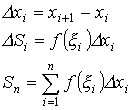
Интегральная
сумма: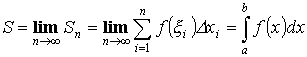
![]()
Определенным интегралом называется предел интегральной суммы.
Т. “О существовании определенного интеграла”.
Если f(x) – непрерывна на отрезке (a,b), то определе нный интеграл существует и не зависит от порядка разбиения и выбора точек.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции.
Свойства определенного интеграла:
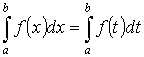
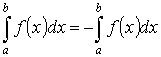
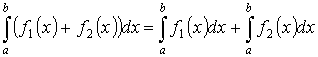

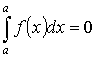
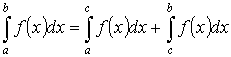 -
аддитивность.
-
аддитивность.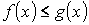 на
на 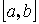
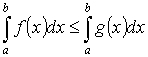
Основные теоремы интегрального исчисления.
Т.1. “об оценке”:
Пусть
y =f(x) интегрируема на [a ,b] ![]() Тогда
Тогда 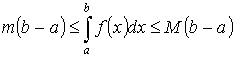
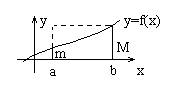
Доказательство:
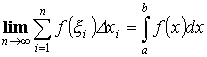
![]()
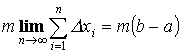
![]()
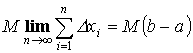
Т.2. “о среднем”
Пусть
y =f(x) интегрируема на [a ,b] Тогда 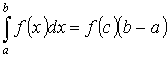 -
где
-
где ![]() f(c) – среднее
значение f(x) на [a
,b].
f(c) – среднее
значение f(x) на [a
,b].
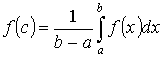
Доказательство:
По
Т.1: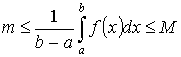
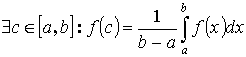
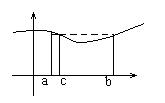
Т.к.
f(x) – непрерывна на [a ,b], то она принимает
все промежуточные значения от m до M.
Следовательно она принимает значение
А. Т.е. существует такая 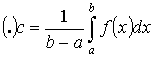
Т.3. “о производной определенного интеграла по переменному верхнему пределу”
Пусть
y =f(x) - интегрируема на [a , b]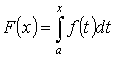
![]() . Тогда
. Тогда ![]()
Доказательство:
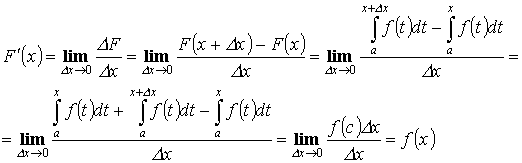
Т.4. “формула Ньютона-Лейбница”
 ,
где F(x) – первообразная для f(x).
,
где F(x) – первообразная для f(x).
Доказательство:
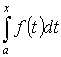 -
первообразная для f(x) по Т.3. Т.к.
первообразные отличаются на const,
то
-
первообразная для f(x) по Т.3. Т.к.
первообразные отличаются на const,
то 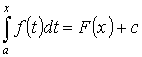 Пусть х=а. F(a)+c=0. c=-F(x). Пусть x=b
Пусть х=а. F(a)+c=0. c=-F(x). Пусть x=b 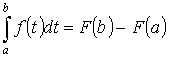
Методы вычисления определенного интеграла.
Замена переменных под знаком определенного интеграла.
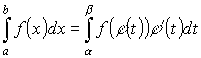
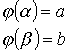
Пример:
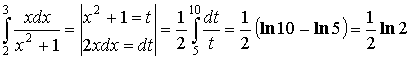
Интегрирование по частям в определенном интеграле.
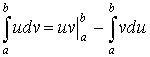
Пример:
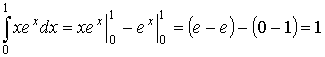
22. Формула Ньютона-Лейбница.
Если
функция f (x) интегрируема
на [a; b],
то для любого ![]() существует
интеграл
существует
интеграл
|
который называется интегралом с переменным верхним пределом.
Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.
Если
функция f интегрируема
на [a; b] и
непрерывна в ![]() то
функция F (x) дифференцируема
в
то
функция F (x) дифференцируема
в ![]() причем
причем
|
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
|
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.
Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:
Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
|
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Пусть f (x) непрерывна
на [a; b], g (t) имеет
непрерывную производную на [α; β], ![]() Тогда
если a = g (α), b = g (β),
то справедлива формула
замены переменной в определенном
интеграле:
Тогда
если a = g (α), b = g (β),
то справедлива формула
замены переменной в определенном
интеграле:
|
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:
|