48.Абсолютный экстремум
Наименьшее (наибольшее) значение функционала во всей области его определения. Если аргумент ограничен некоторыми условиями, описывающими допустимую область изменения, то Э. а. - наименьшее (наибольшее) значение функционала в этой области.
49. Условный экстремум. Метод множителей Лагранжа.
Определение 3. Пусть Е - множество точек X n-мерного евклидова пространства En, для которых выполняются условия
Точка Х0 Еn называется точкой условного экстремума функции у = f(X) относительно соотношений gi(X) = 0, если она является точкой обычного экстремума этой функции, рассматриваемой только на множестве Е. Если система уравнений gi(x1, х2;...; xn) = 0,i = l,2,..., m; m n-m+1;...; хn:
то вопрос об условном экстремуме функции у = f(x1, х2;...; xn) равносилен вопросу об обычном экстремуме функции
На
практике, однако, или принципиально
невозможно выразить из уравнений gi(X)
= 0 группу переменных, или это может
оказаться слишком громоздкой операцией.
В этом случае можно эффективно использовать
метод множителей Лагранжа.
Определение
4. Функция 
,
где 
-
постоянные множители, называется
функцией Лагранжа.
Теорема
6. Если в точке Х0 выполняются
условия: 
,
точка Х0 является
стационарной точкой для функции Лагранжа,
и если второй дифференциал функции
Лагранжа в этой точке является положительно
(отрицательно) определенной квадратичной
формой переменных dx1,
dx2,...,
dxnпри
условии, что они удовлетворяют
соотношениям
то точка Х0 является точкой условного строгого минимума (максимума) для функции у = f(X) относительно условий gi(X) = 0.
50. Геометрические приложения (Касательная прямая и нормальная плоскость к пространственной кривой, к поверхности заданной явно, к поверхности заданной неявно).
51. Двойные интегралы.
52.Свойства двойных интегралов.
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
где R -
область интегрирования в плоскости
Oxy.
Если определенный интеграл 
от
функции одной переменной 
выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R
Формально
двойной интеграл можно ввести как
предел суммы
Римана.
Пусть, для простоты, область
интегрирования R представляет
собой прямоугольник 
(рисунок
2). Используя ряд чисел{ x0, x1,
..., xm }, разобьем
отрезок [a,
b] на
малые интервалы таким образом, чтобы
выполнялось соотношение
Аналогично,
пусть множество чисел 
является
разбиением отрезка [c,
d] вдоль
оси Oy,
при котором справедливы неравенства
Суммой Римана функции f (x,y) над разбиением называется выражение
где 
-
некоторая точка в прямоугольнике 
и 
.
Двойной
интеграл от
функции f (x,y) в
прямоугольной области
определяется
как предел суммы Римана, при котором
максимальные значения Δxi и Δyj стремятся
к нулю:
Чтобы определить двойной интеграл в произвольной области R, отличной от прямоугольной, выберем прямоугольник , покрывающий область R (рисунок 3), и введем функцию g (x,y), такую, что
Тогда двойной интеграл от функции f (x,y) в произвольной области R определяется как
Свойства двойного интеграла
Двойной интеграл обладает следующими свойствами:
,
где k -
константа;
Если
в
области R,
то 
;
Если
в
области R и 
(рисунок
4), то 
;
Если на R и области R и S являются непересекающимися (рисунок 5), то
.
Здесь 
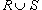означает
объединение этих двух областей.
Пример |
|
Пусть R и S являются непересекающимися областями (рисунок 5). Известны значения двойных интегралов: Оценить
интеграл Решение. Используя свойства двойных интегралов, получаем: |
.