43.Частные производные и дифференциалы высших порядков.

В общем случае частные производные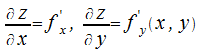 функции - это функции от и . В случае, если они дифференцируемы, то существуют четыре частные производные, которые имеют название частных производных второго порядка:

 

 

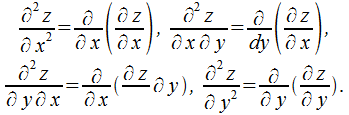
Подобным образом используются частные производные тертьего, …, n-го порядка.

 

О: в качестве частной производной n-го порядка представляется производная первого порядка от частной производной - го порядка.

 

Пример 1:

 

◀

▶

 

Пример 2:

 

◀

▶

 

Заметим, что смешанные производные и , разница между которыми заключается в порядке дифференцирования, являются эквивалентными. В данном случае уместно записать теорему.

 

Т: Частные производные с разным порядком дифференцирования можно назвать равными в т. , если они в этой точке являются непрерывными.

Допустим,

 

 

О: Под дифференциалом второго порядка понимают дифференциал от ее дифференциала первого порядка, который рассматривается в качестве функции переменных и при определенных значениях и .

Подобным образом находятся дифференциалы третьего, …, n-го порядка:

 

 

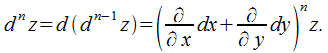
Выражение, заключенное в скобки, формально раскрывается в соответствии с биномиальным законом. Допустим,

 

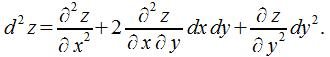
44. Дифференцирование неявных функции.

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

45.Замена переменных в дифференциальных выражениях

Одним из эффективных методов преобразования дифференциальных выражений является переход к новым переменным. Рассмотрим наиболее важные в практическом отношении случаи. 1. Преобразуемое выражение содержит обыкновенные производные:

Если необходимо перейти к новому аргументу t и новой функции и, которые связаны с х и у соотношениями:

то надо подставить эти выражения в W вместе с производными

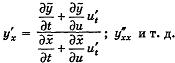
2. Преобразуемое выражение содержит частные производные:

При переходе к новым аргументам t₁ и t₂, которые связаны со старыми х₁ и х₂ соотношениями:

необходимо подставить эти выражения в W вместе с частными производными, которые определяются из следующих уравнений

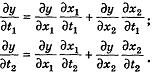
Частные производные высших порядков вычисляются аналогично. Одним из эффективных методов преобразования дифференциальных выражений является переход к новым переменным. Рассмотрим наиболее важные в практическом отношении случаи.