8. Момент силы.

Момент силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведённого из точки О в точку А приложения силы, на силу F.

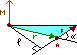
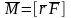, здесь 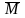- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

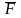Модуль момента силы равен .

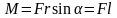Момент силы относительно неподвижной оси z – скалярная величина 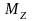, равная проекции на эту ось вектора момента силы, определённого относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на данной оси.

9. Момент инерции твёрдого тела. Теорема Штейнера.

Момент инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n мт системы на квадрат их расстояний до рассматриваемой оси.

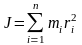, при непрерывном распределении масс: .

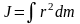Найдём момент инерции однородного сплошного цилиндра:

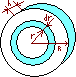
Разобьём цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr, с внутренним радиусом r и внешним – r+dr. Момент инерции каждого полого цилиндра – dJ=r²dm, где dm – масса всего элементарного цилиндра. Его объем - 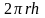dr.

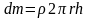dr, и 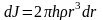. Тогда момент инерции всего цилиндра равен:

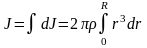
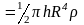, но т.к. 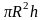-объём, то масса - 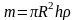, значит:

.

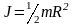Теорема Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J_C относительно параллельной оси, проходящеё через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

.

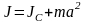10. Основное уравнение динамики вращательного движения.

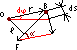
Пусть сила F приложена к точке В. Находящейся от оси вращения на расстоянии r, 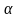-угол между направлением силы и радиус-вектором r. При повороте тела на бесконечно малый угол 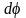, точка приложения В проходит путь 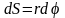, и работа равна произведению проекции силы на направление смещения на величину смещения:

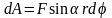, учитывая, что , запишем:

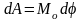, где 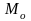-момент силы, относительно оси.

Работа при вращении тела равна произведению момента действующей силы на угол поворота.

Работа при вращении тела идёт на увеличение его кинетической энергии:

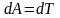, но 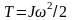, , 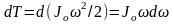поэтому

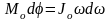, или .

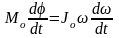Учитывая, что 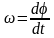получим:

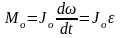, этот и есть уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.

Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то: .

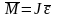11. Момент импульса. Закон сохранения момента импульса.

Момент импульса (количество движения) мт А относительно неподвижной точки О – физическая величина, определяемая векторным произведением:

,

где r-радиус-вектор, проведённый из точки О в точку А; 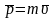- импульс мт. 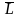-псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

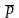Модуль вектора момента импульса:

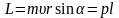
Момент импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси.

Т.к. 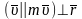, то момент импульса отдельной частицы:

.

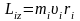Момент импульса твёрдого тела относительно оси есть сумма моментов импульса отдельных частиц, а т.к. 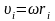, то:

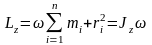, т.о. момент импульса твёрдого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем последнее уравнение:

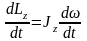
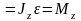
, т.е.: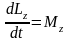

это и есть уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси: Производная момента импульса твёрдого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство:

.

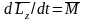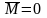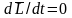В замкнутой системе момент внешних сил и , откуда: L=const, это выражение и есть закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.