c1)Мат.моделью эк-ой задачи называется совокупность мат. Соотношений, описывающих рассматриваемый эк-ий процесс. Для составления мат. Модели необходимо: 1) выбрать переменные задачи 2) составить сис-му ограничений 3) задать целевую ф-ию.

Переменными задачи называются величины , характеризующие эк-ий процесс.

Их записывают в виде вектора

Сис-мой ограничений называется совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов,

например условия положительных переменных. их вид:

Целевая ф-ия-это ф-ия , характеризующая качество выполнения задачи и экстремум которой требуется найти.

Общая задача мат. Программирования формируется след. образом: найти переменные задачи которые обеспечивают экстремум целевой ф-ии (1)

И удовлетворяют сис-ме ограничений (2)

Если целевая ф-ия 1 и сис-ма ограничений 2 линейны, то задача мат. програм-рования -задача ЛП

Допустимым решением(планом) зад. ЛП наз-ся любой n-мерный вектор удовлетворяющий сис-ме огран-ний и услов-м неотрицат-ти. Множество допуст-ых решений задачи образует область допустимых решений. Оптим. Решением зад. ЛП называется план задачи, при котором целевая ф-ия достигает экстремума.

Примеры задач:

1)Задача о наил. Использовании ресурсов. Пусть предприятие может выпускать n-видов прод-ии П1,…,Пn. При этом исп-ся М видов ресурсов R1,…,Rm. Пусть Aijкол-во i-го ресурса, расходующегося на про-во единицы jой пр-ии. Сj-цена реализации ед. jой пр-ии. Bi-запса i-uj ресурса.Нужно найти план с макс. прибылью.Пусть Xj-план выпуска J-ой пр-ии получаем=>ЗЛП:

F(x)= -цена реализации продукции, которая должна быть max. Теперь ограничение по ресурсам (показывает сколько ресурса мы израсходовали) получим симметричное ЗЛП.

2)Задача о выборе оптимальной технологи. Пусть при про-ве пр-ии использ-ся n-видов технологий. Запасы ресурсов эффетивность использования J-ой технологии за ед. времени ; Cj , j=1,..,n; Aij-расход i-го ресурса по J-ой технологии в ед. времени. Xj-время использования j-ой технологии. Составим опт. План использ. Технологий(зад. На макс) Xj ; Xj

3)Задача о диете. Есть n-видов продуктов, содержащих m видов питательных вещ-в. -кол-во ед. i-го пит. Вещ-ва, содержащегося в ед. j-го продукта Cj- стоимость ед j-го прод-та. Кроме того требуется чтобы наш рацион содержал не менее Bi единиц i-го питат. Вещ-ва. Задача на минимум. Xj- кол-во j-го продукта. ;

4)Транспортная задача Есть m пунктов про-ва, в к-ых сосредоточено Ai ед. однородного груза, кроме того есть n пунктов назначения при чём потребности потребителей равны Bj, j=1,…,n

Кроме того, известно Cij-стоимость перевозки ед. пр-ии i-го поставщика к j-ому потребителю. Нужен план с min транспортными расходами. Xij –объём перевозок i-го постав. К j-му потреб.

Суммарный трансп. Расход: мы должны развести весь груз

• Составим систему1) и 2)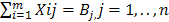

Xij каноническая форма записи

2. Общая задача линейного программирования. Графический метод решения задач лп.

Общей ЗЛП называется задача

f(x)= c1x1+…+cn x n – min (max) (1)

при условии, что переменные удовлетворяют системе линейных равенств и неравенств:

(2)

; j=1,…,n (3)

Функция f(x) называется целевой функцией.

Система (2) – это и есть система ограничений.

Условие 3 – условие неотрицательности, которое следует из экономического смысла задачи.

Графический метод решений ЗЛП.

Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства.

Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные.

F(x) = c1x1+c2x2 – max

И на координатной плоскости построим допустимую многоугольную область, соответствующую этим ограничениям

Случаи, которые могут получиться:

1. Основной случай - получающаяся область имеет вид ограниченного (замкнутого) выпуклого многоугольника (см. рис. 1).

2. Неосновной случай - получается неограниченный (незамкнутый) выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 2

3. Наконец, возможен случай, когда неравенства противоречат друг другу, и допустимая область вообще пуста.

3) Формы записи задачи ЛП

Общей задачей ЛП, называется задача

П ри условиях, что

i =1, …, m₁ (2)

i= m₁+1, … m₂

i= m₁+1, … m₂

j=1, …, n (3)

Функция f(x) называется целевой функцией. Система (2) – система ограничений, условие (3) – условие неотрицательности, которое следует из экономического смысла задачи. Симметричной формой записи задачи ЛП называют задачу:

(4)

(5)

j=1, …, n (6)

Если задача решается на максимум, то имеются ограничения типа ≤

(7)

i=1, …, m (8)

j =1, …, n (9)

Канонической формой записи задачи называют задачу:

(11)

j=1, …, n (12)

Симмитричная форма записи сводится к канонической.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти минимум функции , можно перейти к нахождению максимума функции , поскольку

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.