21. Замечательные пределы.

Первый замечательный предел:

Второй замечательный предел:

22.Понятие производной функции в точке в физическом смысле производные функции в физическом смысле мгновенну. скор. некоторой точки наз. производной функции s(t)

23. Алгебрарическое понятие производной и ее свойства в алгебравическом смысле: предел разностного отношения приращения функ. к приращению аргумента при условии ,что дельта x стремится к 0,наз. производной функ. f(x) в некоторой зад. точке .

24. геометрический смысл производной. углом между прямой и осью Ох называется углом между положительно направленной оси Ох и заданной прямой производной в геометрическом смысле называют угловой коэффициент касательной построенный к заданной функции ,к заданной точке. f(x)=f(x0)+f'(x)(x-x0)

25. Уравнение касательной и её вычисление

- уравнение касательной

1. Найти f(х0). 2. Найти f (x0) и f '(х0). 3. Подставить найденные числа f(х0), f '(х0) в общее уравнение касательной

26. Вторая производная и ее физический смысл.

В торая производная определяет скорость изменения скорости или ускорение. Так, если x – координата материальной точки, движущейся со скоростью

т о ускорение этой точки равно

27)Применение производной к исследованию и построению гр.Функции.

1)ООФ-те значения аргумента,при кот. функция имеет смысл.

2)МЗФ

3)Нули функции(точки пересечения графика с осью Ох)

4)Чётность-чётная(гр. симетричен относительно оси Оу);нечёт.-относительно началу координат.(общего вида-не все знаки меняются)

5)Период

6)Стационарные точки-точки в которых первая производная равна 0.

7)Монотонность.Если 1-ая производная на некотором интервале положительна,то функция на этом интервале явл. возрастающей,если 1 производная отриц. то функция убывающая.Точки при переходе через кот. одна производная меняет знак наз. экстремальными точками.Если производная меняет знак с "+" на "-" точка наз. точкой максимума.Если при переходе через некот. точку первая производная меняет знак с "-" на "+" точка наз. точкой минимума.Если знак производнй НЕ меняется,то эта стационарная точка,НО НЕ экстремальная.

8)Выпуклость графика.Выпуклость графика фуекции опред. с помощью второй производной,кот. берётся от 1-ой производной и имеет те же св-ва что и 1-ая производная.

Если на некот. интервале 2-ая производная отрицательная то график функции выпуклый вверх,если же 2-ая производная больше 0,то график функ. вогнутый.

9)ищем доп.точки по мере необходимости

28. Понятие первообразной.

Первообразной данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

29. Определение неопределенного интеграла и его основные свойства.

Неопределённый интеграл для функции   — это совокупность всех первообразных данной функции.

Если функция   определена и непрерывна на промежутке   и   — её первообразная, то есть   при  , то

  , где С — произвольная постоянная.

Свойства.

30. Способы вычисления неопределенных интегралов.

Метод введения нового аргумента. Если

то

Метод разложения. Если

то

Метод подстановки. Если   — непрерывна, то, полагая

получим

Метод интегрирования по частям. Если   и   — некоторые дифференцируемые функции от  , то

31. Определенный интеграл как площадь криволинейной трапеции.

Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой функции  , осью   и прямыми  ,  :

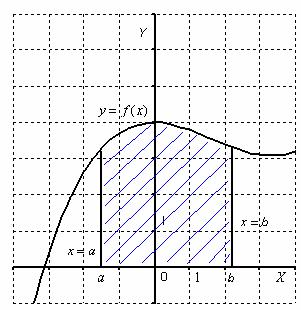
Площадь криволинейной трапеции численно равна определенному интегралу  .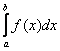

32. Применение определенного интеграла

1. Вычисление площади плоской фигуры в прямоугольных координатах.

2. Вычисление площади плоской фигуры в полярных координатах.

3. Вычисление объема тела вращения.

4. Вычисление длины дуги кривой.

5. Вычисление площади поверхности тела вращения.

33. Основные понятия стереометрии.

1.Точка- абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других измеримых характеристик. Таким образом, точкой называют нульмерный объект.

2.Прямая- прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками

3. Плоскость- поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;

а. Две плоскости являются либо параллельными, либо пересекаются по прямой.

б. Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.

в.Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.

г. Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.