Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию [pdf]

деления суммы asn-1+c на m, и вместе с последовательностью s0, s1,…

выборе a, c, m, s0 последовательность r0, r1,… будет хорошо имитировать последовательность равномерно распределенных в интервале (0, 1) случайных чисел. Одним из таких выборов оказывается следующий:

1) m = 2k ,где k берется настолько большим, насколько это возможно (надо иметь в виду, что последовательность s0, s1, …, равно как и последовательность r0, r1, …, будет периодической с периодом 2k; при небольших значениях k периодичность будет слишком заметной )

2) При делении a на 8 должен получаться остаток 5. Кроме

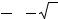
3) Число c должно быть нечетным; при этом желательно, чтобы

4) Число s0 можно выбирать произвольно в диапазоне от 0 до

m – 1.

В связи со сказанным предполагаются следующие задания: a) Подобрать несколько вариантов троек a, c, m,

удовлетворяющих условиям 1) – 3).

б) Найти еще какое-нибудь соображение, позволяющее хорошо имитировать случайность, и на его основе описать новый датчик.

в) Пользуясь различными датчиками, среди которых должны быть датчики, построенные по предложенной выше схеме с различным выбором a, c, m, s0, и «самодельные» датчики, построенные на других соображениях, требуется провести эксперименты , описанные в предыдущей задаче.

749. Датчики случайных чисел находят интересное применение в вычислении площадей и объемов: на этом принципе основан известный метод Монте-Карло (объяснение происхождения названия и подробное изложение самого метода с многочисленными примерами изложений имеется, например, в [47]). Пусть задана фигура M, целиком лежащая внутри единичного квадрата, и пусть нужно вычислить ее площадь. Пусть в единичном квадрате выбрано наугад n точек (рис. 42) и пусть v(n) – число точек, попавших внутрь M. Тогда геометрически ясно, что при больших n площадь фигуры M будет

приблизительно равна v(n)/n и чем больше будет n, тем ближе мы подойдем к истинному значению площади. В качестве выбираемых «наугад» точек в этих вычислениях можно взять точки с координатами (r0, r1), (r2, r3), …, где в роли r0, r1,… выступают числа, получаемые с помощью датчика случайных чисел, равномерно распределенных в интервале (0, 1).

Аналогично, беря точки с координатами (r0, r1, r2), (r3, r4, r5), …, можно вычислять объемы тел, целиком лежащие внутри единичного куба (рис. 43).

В связи с методом Монте-Карло предлагаются следующие задания. Воспользовавшись несколькими датчиками (в крайнем случае одним датчиком):

а) определить площадь круга (x – 0.5)2+(y – 0.5)2 < 1/4; для этого найти по 200 точек с помощью каждого из датчиков; ответы сравнить с

π 4 ;

б) определить объем шара (x – 0.5)2+(y – 0.5)2+(z – 0.5)2 < 1/4;

для этого найти по 200 точек с помощью каждого из датчиков; ответы сравнить сπ 6 .

750. Случайная числовая последовательность r0 , r1, … , члены которой равномерно распределены в интервале (0, 1), может быть использована для построения случайной последовательности v0 , v1 , …, члены которой принадлежат конечному множеству, состоящему из элементов x1 , … , xn . Элементы x1 , …, xn повторяются в последовательности v0 , v1,… с заданными частотами, соответственно равными p1, …, pn (т.е. относительно последовательности v0 , v1,… можно считать, что xi встречается в ней с вероятностью pi (i=1, 2, … , n) p1+…+ pn=1 ). Последовательность v0 , v1, … будем называть

Для построения v0, v1, … используется следующий прием [47].

Интервал (0, 1) разбиваем на n интервалов, длины которых равны p1 , … , pn . Координаты точек разбиения будут p1 , p1+ p2 , p1+ p2+ p3, …, p1+ p2+...+ pn-1. Полученные интервалы обозначаем через I1 , … , In.

Теперь перебираем числа r0, r1, r2, …., и если очередное число rk

попадает в интервал Ij (1≤ j ≤ n) , то в качестве vk берем xj (в силу равномерного распределения членов последовательности r0, r1, … в интервале (0 , 1) вероятность попадания rk в некоторый интервал равна длине этого интервала). Если вдруг окажется, что rk совпадает с точкой разбиения (концом интервала), то можно условно считать, что число rk попало в интервал, лежащий справа от него.

Предлагаются следующие задания, в которых надо воспользоваться датчиком случайных чисел:

а) Построить 100 первых членов случайной последовательности из нулей и единиц, в которой нуль и единица равновероятны, т. е.

в) Построить 100 первых членов случайной последовательности из нулей и единиц, в которой нуль встречается с вероятностью 1/4, а единица – с вероятностью 3/4, т. е. последовательности с

г) Построить 100 первых членов случайной последовательности из слов «камень», «ножницы», «бумага», в которой эти три слова равновероятны, т. е. последовательности с распределением

использовать для выбора ходов в известной игре «камень, ножницы, бумага».)

д) Построить 100 первых членов случайной последовательности из слов «камень», «ножницы», «бумага», в которой слово «камень» встречается с вероятностью 1/3, слово «ножницы» – с вероятностью 1/2, слово «бумага» – с вероятностью 1/6 , т. е. последовательности с

можно использовать для выбора ходов в известной игре «камень, ножницы, бумага» со следующей системой премий: когда «камень» тупит «ножницы», присуждается одно очко, когда «ножницы» режут «бумагу», присуждается два очка, когда «бумага» покрывает «камень», присуждается три очка.) *)

*) Указанные в заданиях г) и д) стратегии чередования ходов, основанные на случайных последовательностях, является в определенном смысле оптимальными. См. об этом, например, в книге

[33].

751. Для наглядной демонстрации некоторых законов теории вероятностей используется прибор, называемый доской Гальтона (рис. 44). Металлические шарики по очереди попадают в верхний канал; встретив препятствие они должны выбрать путь налево или направо, затем проходить второй выбор и т. д. Каждый из выборов случаен, каждая из вероятностей выбора пути налево и направо равна 1/2. При достаточно высоком качестве прибора наблюдаемая картина распределения шариков в нижних отделениях доски Гальтона хорошо согласуется с вероятностными расчетами, по которым количества шариков, оказавшихся в отделениях, пронумерованных числами 1, …, m (на рис.44 m=5), должны быть пропорциональными (с некоторым

коэффициентом пропорциональности, зависящим от общего числа шариков) числам из m-й строки треугольника Паскаля (см. задачу 555). Кривая, огибающая верхушки столбцов из шариков, должна иметь колоколообразную форму (рис. 45). Путь шарика по доске Гальтона, содержащей m нижних отделений, можно изобразить группой из m нулей и единиц: нуль изображает выбор пути налево, единица - направо. Получив с помощью датчика случайных чисел mn членов случайной последовательности v0, v1, … из нулей и единиц с

(vm, …, v2m-1), …, (v(n-1)m, …, vnm), мы получим изображения путей n воображаемых шариков. Номер отделения, в которое попадает шарик, определяется по количеству единиц в изображении маршрута. Пусть даны натуральные n и m (n≥ 2m). Требуется подсчитать, исходя из модели, которая основана на датчике случайных чисел, количество