
Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию [pdf]
.pdf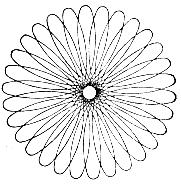
Даны натуральные A, B, D (D < B < A). Составить программу, моделирующую спирограф.
Рис. 72
854. Построить на экране множество точек, координаты которых удовлетворяют следующим неравенствам или системам неравенств:
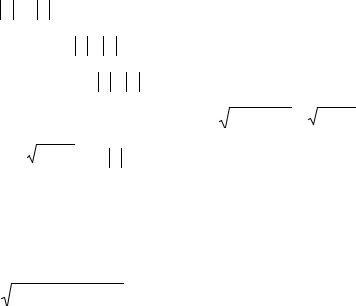
а) y + 2 x ≤ x2 + 1; |
|
б) x2 + y2 ≤ 2( x + y ) ; |
|
в) 4 ≤ x2 + y2 ≤ 2( x + y ) ; |
|
г) log1/ 3 (2x + y − 2) > log1/ 3 ( y + 1) , |
y − 2x − 3 < 3 − 2x ; |
д) y ≥ 1− x2 , y + x ≤ 4 ; |
|
е) 2 y − x2 < 0, x2 − y 2 ≥ 0 ;
ж) y ≥ x2 − 4x + 3, y < x2 + 4x + 3 ;
з) 2 y ≥ x2 , y ≤ − 2x2 + 3x ;
и) x2 − 3y 2 + 4x + 4 ≤ 2x + 1, x2 + y 2 ≤ 4 .
855. Кривые дракона, показанные на рис. 73, а -73, в, могут быть построены с помощью следующего рекуррентного метода.
Каждой кривой ставится в соответствие последовательность, состоящая из нулей и единиц (будем называть ее двоичной формулой), где единица соответствует повороту кривой налево, а нуль - повороту направо. Кривая дракона первого порядка имеет двоичную формулу 1 (рис. 73, а). Для того чтобы получить двоичную формулу кривой дракона каждого следующего порядка, следует приписать справа к формуле кривой предыдущего порядка единицу. Полученная последовательность дает половину искомой формулы. Затем в последовательности цифр, предшествующих приписанной единице, следует заменить на нуль единицу, стоящую в ее середине, после чего приписать полученную последовательность справа от уже построенной части формулы. На рис. 73, б показана кривая дракона второго порядка, которой соответствует двоичная формула 110, а на рис. 73, в - кривая дракона третьего порядка - ей соответствует двоичная формула 1101100. Кривые строятся от хвоста к голове дракона и повернуты так,
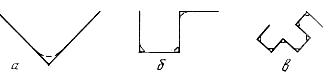
чтобы драконы «плыли» направо, а пасть и кончик хвоста касались «поверхности воды». Прямые углы обычно скругляются дугой окружности или срезаются (показано на рис. 73, а -73, в штриховой линией) для того, чтобы вершины углов не соприкасались и не создавалась иллюзия самопересечения кривой.
Дано натуральное п. Получить кривую дракона порядка п.
Рис. 73
856. Построить изображения, приведенные на рис. 74, применив какой-нибудь способ раскраски.
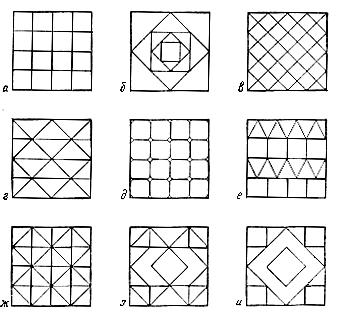
Рис. 74
857. Даны натуральные числа п и r. Построить п точек, являющихся вершинами правильного n - угольника, вписанного в
окружность радиуса r, и соединить каждую из точек со всеми остальными n-1 точками. Координаты точек задаются формулами xi = r cos(2π i / n), yi = r sin(2π i / n)(i = 1,2,...,n) .
Во избежание повторного вычерчивания линий, соединяющих одни и те же точки, каждую точку с номером i следует соединять только с теми точками с номерами j, для которых выполнено условие i < j.
858. Дано натуральное число r. Построить фигуры, построенные на рис. 75, а - 75, г. Фигуры образованы окружностью радиуса r и восемью точками, являющимися вершинами правильного многоугольника, вписанного в эту окружность, и соединенных между собой определенным образом. Фигура на рис. 75, а - это правильный восьмиугольник, образованный последовательным соединением его вершин. Для построения фигуры на рис. 75, б следует соединять вершины многоугольника через одну. При построении фигуры на рис.
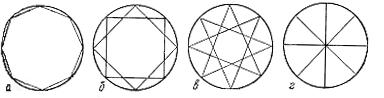
75, в соединяются вершины, отстоящие друг от друга на две вершины, а при построении фигуры на рис. 75, г - отстоящие на три вершины.
Рис. 75
859. Даны натуральные числа п и r. Построить квадрат, длина стороны которого равна r. Разместить по одной точке в каждом углу квадрата и по n-1 точек на каждой его стороне. Расстояния между соседними точками на любой из сторон должны быть одинаковыми и равными r/п. Тем самым будет построено всего 4n точек, которые можно занумеровать числами 1, ..., 4n (нумерация начинается с левого верхнего угла квадрата и выполняется последовательно). Соединить каждую точку с номером i со всеми точками с номерами j (i, j = 1, ...,
4n) такими, что j > i и разность j-i есть число Фибоначчи, меньшее 4n (см. задачу 144).
860. Уравнение f (х, у)=0, представляющее все точки (x, у) некоторой кривой, называют уравнением кривой в неявной форме. Если кривая делит плоскость на две части, то уравнение в неявной форме позволяет определить, лежит ли точка на кривой, или если нет, то в какой части она лежит (см. задачу 52).
Даны натуральные числа r, xc , уc , n, a0 ,..., a2n -1 . Числа r, xc , уc задают окружность радиуса r с центром в точке (xc , уc). Пары чисел ai, ai+1 (i кратно 2) являются координатами точек.
а) Построить окружность и все точки, заданные последовательностью a0 ,..., a2n -1 и лежащие вне окружности.
б) Построить окружность и все точки, заданные последовательностью a0 ,..., a2n -1 и лежащие внутри окружности.

в) Построить окружность и все точки, заданные последовательностью a0 ,..., a2n -1 и не принадлежащие окружности. Точки, лежащие вне окружности и внутри нее, должны иметь разные цвета.
861. Даны натуральные числа a, b, c, n, a0 ,..., a2n -1. Числа a, b, c задают прямую l с уравнением ax + by + c = 0. Пары чисел ai , ai+1 (i кратно 2) являются координатами точек.
а) Построить прямую l и все точки, заданные последовательностью a0 ,..., a2n -1 и такие, что ax + by + c < 0.
б) Построить прямую l и все точки, заданные последовательностью a0 ,..., a2n -1 и такие, что ax + by + c > 0.
в) Построить прямую l и все точки, заданные последовательностью a0 ,..., a2n -1 и не принадлежащие прямой l. Точки, лежащие по разные стороны от прямой, должны иметь разные цвета.
862. Уравнение прямой в неявной форме (см. задачу 860) имеет весьма полезное свойство: f (x, y)
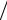 (a2 + b2 ) равно длине
(a2 + b2 ) равно длине

перпендикуляра от точки (х, у) к прямой. Например, если f (x, y) = - x + 2y + 2, то длина перпендикуляра, опущенного на прямую из точки
(0,1), равна f (0,1)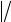 5 = 4
5 = 4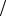 5 .
5 .
Даны натуральные числа a, b, c, n, a0 ,..., a2n -1 действительное число r. Числа a, b, c определяют прямую с уравнением ax + by + c = 0.
Пары чисел ai , ai+ 1 (i кратно 2) являются координатами точек.
а) Построить прямую l и все точки, заданные последовательностью a0 ,..., a2n -1, не принадлежащие прямой l такие, что длина перпендикуляра, опущенного из точки на прямую, меньше r.
б) Построить прямую l и все точки, заданные последовательностью a0 ,..., a2n -1, не принадлежащие прямой l такие, что длина перпендикуляра, опущенного из точки на прямую, больше r.
в) Построить прямую l и все точки, заданные последовательностью a0 ,..., a2n -1 и не принадлежащие прямой l. Точки,
