Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию [pdf]
.pdf844. Построить графики функций: |
|
|
|
|
|
а) y = 3x2 ; |
б) y = − 6x2 + 3x ; |
||||
в) y = x3 + 2x2 + x ; |
г) y = x5 ; |
||||
д) y = sin x ; |
е) y = cos(x − 1) + |
|
x |
|
. |
|
|
||||
845. Построить графики функций, указанных в задаче 337. 846. Исследовать область определения и построить графики
следующих функций:
а) y = |
|
1 |
|
; |
|
|
|
|
|
|
|
|
б) y = |
|
x + 3 |
; |
|
|
|
в) y = 3 + |
2 |
+ |
3 |
; |
||
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
x2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 2 |
|
|
|
|
|
|||||||
г) y = |
3 − |
|
2 |
− |
3 |
; |
|
|
|
д) y = |
|
1 |
|
|
|
; |
|
|
|
|
||||||
|
|
x2 |
|
|
|
|
|
3x2 + 2x + 1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
е) y = |
|
|
|
1 |
|
|
|
; |
|
ж) y = |
1 |
|
; |
|
|
|
|
|
||||||||
|
x2 + 2x + 1 |
|
|
|
|
x2 + 3x + 1 |
|
|
|
|
|
|||||||||||||||
з) y = |
|
|
|
|
|
x |
|
|
|
|
|
; |
и) y = |
|
|
x |
; |
|
|
|
|
|
||||
|
3x2 + 2x + 1 |
|
|
x2 + 2x + 1 |
|
|
|
|
|
|
||||||||||||||||
к) y = |
x |
|
л) y = |
x |
|
м) y = |
x |
|
|
; |
|
; |
|
. |
|||
x2 − 2x + 1 |
x2 + 3x + 1 |
x2 − 3x + 1 |
||||||
847. Построить кривые по заданному параметрическому представлению*).
а) Окружность радиуса r с центром в начале координат: х = r
соs t, y = r sin t, t [0, 2π ).
б) Эллипс с большой и малой полуосями, равными со-
ответственно r1 и r2 и расположенными параллельно осям координат:
х= r1 cos t, у = r2 sin t, t [0,2π ). .
в) Улитка Паскаля (рис. 58): |
|
|
|
x = acos2 t + bcost, y = a cost sint + b sint, |
a > 0, |
b > 0, |
t [0,2π ) . |
Рассмотреть случаи, когда b ≥ 2a,a < b < |
2a,a > |
b . |
|
г) Кардиоида (рис. 59): x = a cos t (1 + cos t), |
y = a sin t (1 + |
||
cost), a>0, t [0,2π ). |
|
|
|
д) Эпициклоида (рис. 60): х = (а+b) соs t - а соs ((а+b) t/а), у =
(а + b) sin t - а sin ((a + b) t/a), а > 0, b > 0. Рассмотреть следующие случаи:
1) если b/a есть целое положительное число, t [0, 2π ) ;
Рис. 60
2) если b/a = р/q, где р и q -положительные целые взаимно простые числа, t [0, 2qπ ).
е) Астроида (рис. 61): x = bcos3 t, y = bsin 3 t, t [0,2π ).
ж) Циссоида (рис. 62):
x = at 2 /(1+ t 2 ), y = at 3 /(1+ t 2 ), t (−∞ , ∞ ),a > 0.
Рис. 61 |
Рис. 62 |
Рис. 63 |
3) Строфоида (рис. 63): |
|
|
x = a(t2 − 1) /(t2 + 1),y = at(t2 − 1) /(t2 + 1),y = at(t2 − 1) /(t 2 + 1),t (−∞ , ∞ ),a > |
0 |
|
. |
и) Конхоида Никомеда (рис. 64): х = a+ l соs t, y = а tg t+l sin t, |
|
t |
(− π / 2,π / 2) - правая ветвь, t (π / 2,3π / 2) - левая ветвь, a > 0, l > 0. |
|
Рассмотреть случаи, когда l < a, l > a, l = a.
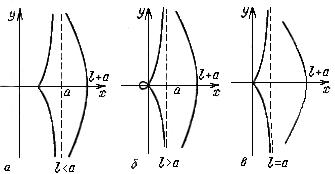
Рис. 64
*) Параметрическое представление кривой l на плоскости с координатами х, y -это две функции х = х(t), у = у(t), определенные на одном и том же числовом множестве.
848. Построить кривые по их уравнениям в полярных координатах *).
*) Полярные координаты ρ ,ϕ точки М на плоскости - это расстояние
ρ =ОМ от фиксированной точки O (полюса) до точки М и угол ϕ =
=
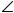РОМ между ОМ и полярной осью (полупрямой) ОР (рис. 68).
Рис. 68
а) Овалы Кассини (рис. 65):
ρ 2 = c2 cos 2ϕ ± 
c4 cos2 2ϕ + (a4 − c4 )
Рассмотреть случаи, когда a > c
2 > 0,0 < c < a < c 
2,0 < a < c .
Рис. 65
б) Лемниската (рис. 66): ρ = a 2cos 2ϕ , a > 0 .
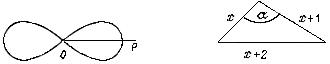
Рис. 66 Рис. 67
849. Рассмотрим треугольник со сторонами x, х+ 1, х+2, где x - некоторое действительное число (рис. 67).
Угол α между сторонами х и x+ 1 является функцией от х. Исследовать область определения и построить график этой функции.
850. Вычерчивание окружности, заданной параметрическими уравнениями x = r cos t , y = r sin t, t [0,2π ) (см. предыдущую
задачу), выполняется довольно медленно в связи с необходимостью вычисления тригонометрических функций. Процесс можно ускорить, если воспользоваться параметрическими уравнениями
x = xc + r |
|
1 |
− |
t 2 |
, |
y = yc + r |
2t |
, t [0,1) . |
|
1 |
+ |
t 2 |
1+ t 2 |
||||||
|
|
|
|
||||||
Указанное изменение параметра соответствует дуге окружности от 0 до π / 2 . Полная окружность может быть построена симметричным отображением каждой полученной точки относительно оси ОХ, оси ОY и начала координат в предположении, что начало координат совмещено с центром окружности (рис. 69).
Даны натуральные xc , yc , r . Построить окружность с центром в точке ( xc , yc ) и радиусом r, воспользовавшись алгоритмом,
описанным выше.
Рис. 69 |
Рис.70 |
851. Построить спираль вокруг начала координат с п витками и
853. Спирограф - это зубчатый диск радиуса B, расположенный внутри колеса радиуса А. Диск вращается против часовой стрелки и всегда находится в зацеплении с внешним колесом. В диске имеется небольшое отверстие на расстоянии D от центра диска, в которое помещается карандаш. Грифель карандаша в процессе вращения вычерчивает рисунок ; вычерчивание заканчивается, когда карандаш возвращается в исходное положение. С помощью спирографа могут быть построены рисунки, подобные приведенному на рис. 72 .
Уравнение кривой, вычерчиваемой грифелем, в параметрической форме имеет вид
x = (A-B) cos t + D cosϕ ,
y = (A-B) sin t - D sinϕ , где ϕ = ( A /B) t, D < B < A.
Угол t меняется от 0 до 2π n , п равно B, деленному на наибольший общий делитель (НОД) В и А (см. задачу 89).