
Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию [pdf]
.pdf619. Эта задача является обобщением предыдущей. Рассматривается n лучей, проведенных в плоскости из точки О (n ≥ 2). Углы между соседними лучами равны 2π /n. Вновь на лучах выбираются точки А1, …, Аn и проводятся соответствующие окружности. Считая данными расстояния А1О, А2О, …, АnО, вычислить площадь фигуры, аналогичной описанной в предыдущей задаче.
620. Медианой множества, состоящего из четного числа точек плоскости, никакие три из которых не лежат на одной прямой, называется прямая, соединяющая две точки множества, с обеих сторон от которой лежит равное число точек.
Даны действительные числа x1, y1, x2, y2, …, xn, yn (n—нечетное число). Найти число медиан множества точек с координатами (x1, y1), (x2, y2), …, (xn, yn) в предположении, что никакие три точки этого множества не лежат на одной прямой.
621. Даны действительные числа a, b, c, d. Выяснить, можно ли прямоугольник со сторонами a, b целиком уместить в прямоугольнике со сторонами c, d (в отличие от задачи 55, здесь не обязательна взаимная параллельность сторон).
622. Даны действительные числа a1, b1, c1, a2, b2, c2, …, an, bn, cn. Эта последовательность определяет на плоскости n квадратов со сторонами, параллельными осям: ai, bi – координаты центра квадрата, ci – длина его стороны (i =1, …, n). Определить площадь фигуры, образованной всеми квадратами (рис. 31).
Здесь может оказаться полезным предварительное решение следующей задачи.
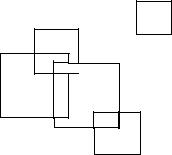
Стороны двух прямоугольников параллельны координатным осям. Каждый из прямоугольников задан четырьмя действительными числами – двумя абсциссами и двумя ординатами. Представить ту часть первого прямоугольника, которая не покрывается вторым прямоугольником, в виде объединения нескольких прямоугольников, не накладывающихся друг на друга.
Рис. 31
623. Даны действительные числа x, y. В треугольнике, вершинами которого служат точки (0, 0), (0, 1), (x, y), найти точку (для
определения ее координат разрешается использовать методы приближенных вычислений), сумма расстояний от которой до вершин треугольника минимальна. Известно (теорема Штейнера), что для треугольника с углами, не превосходящими 2π /3 (т. е. 120° ), эта точка совпадает с точкой Торричелли, т. е. точкой, из которой все стороны треугольника видны под углом 2π /3. Если же в треугольнике имеется угол, больший 2π /3, то решением задачи будет вершина этого угла.
624. Даны действительные числа x1, y1, x2, y2, …, xn, yn. Известно, что точки p1, p2, …, pn с координатами (x1, y1), (x2, y2), …, (xn, yn) попарно различны. Рассмотрим замкнутую ломаную p1 p2…pn.
а) Верно ли, что ломаная не имеет самопересечений?
б) В предположении, что ломаная не имеет самопересечений, выяснить, является ли n-угольник p1 p2…pn выпуклым.
625. Даны действительные числа x1, y1, x2, y2, …, xn, yn. Известно, что точки p1, p2, …, pn с координатами (x1, y1), (x2, y2), …, (xn,
yn) попарно различны. Найти выпуклый многоугольник с вершинами в некоторых из точек p1, p2, …, pn, который содержит все точки p1, p2, …,
pn. Многоугольник должен быть представлен последовательностью |
|
|
вершин. |
|
|
626. Сетью называется совокупность точек (узлов), |
|
|
некоторые из которых соединены между собой стрелками. |
|
|
Сети, состоящие из n узлов, можно сопоставить две квадратные |
|
|
матрицы порядка n: матрицу соединений и матрицу связей. |
|
|
Элемент матрицы соединений aij равен 1, если сеть содержит |
|
|
стрелку, ведущую из узла i в узел j, и 0 в |
3 |
|
1 |
|
|
противном случае. Элемент bij матрицы |
5 |
6 |
связей равен 1, если из узла i можно |
|
|
попасть в узел j, двигаясь по стрелкам, и 0 |
4 |
|
2 |
|
|
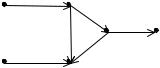
в противном случае. Так, для сети, |
Рис. 32 |
|
изображенной на рис.32, матрицы соединений и связей имеют вид
é0 0 1 0 0 0ù |
|
é0 0 1 1 1 1ù |
||||
ê |
ú |
|
ê |
|
ú |
|
ê0 0 0 1 0 0ú |
|
ê0 0 0 1 0 0ú |
||||
ê0 0 0 1 1 0ú , |
|
ê0 0 0 1 1 |
1ú . |
|||
ê |
ú |
|
ê |
|
ú |
|
ê0 0 0 0 0 0ú |
|
ê0 0 0 0 0 |
0ú |
|||
ê0 0 0 1 0 1ú |
|
ê0 0 0 1 0 |
1ú |
|||
ê |
ú |
|
ê |
|
ú |
|
ëê0 0 0 0 0 0ûú |
|
ëê0 0 0 0 0 |
0ûú |
|||
Дана матрица соединений некоторой сети из n узлов; получить |
||||||
матрицу связей этой сети. |
|
|
|
|
||
627. Линия называется уникурсальной, |
|
3 |
|
|
||
если ее можно начертить, не отрывая |
2 |
|
4 |
|||
|
||||||
карандаша от бумаги и не проходя два раза |
1 |
6 |
5 |
|||
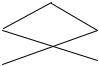
одно и тоже звено. Доказать, что линия |
Рис. 33 |
|||||
|
|
|
||||
уникурсальна тогда и только тогда, когда число тех ее узлов, из которых выходит нечетное число звеньев, не превосходит двух. Линии, содержащей n узлов, можно сопоставить квадратную матрицу порядка
n – матрицу соединений, элемент aij которой равен 1, если узел i соединен с узлом j некоторым звеном, не содержащим других вершин, и 0 в противном случае (i, j=1, …, n). Для линии, изображенной на рис. 33, матрица соединений имеет вид
é0 |
1 |
0 |
0 |
1 |
1ù |
ê |
0 |
1 |
1 |
0 |
ú |
ê1 |
1ú |
||||
ê0 |
1 |
0 |
1 |
0 |
0ú . |
ê |
1 |
1 |
0 |
1 |
ú |
ê0 |
1ú |
||||
ê1 |
0 |
0 |
1 |
0 |
1ú |
ê |
1 |
0 |
1 |
1 |
ú |
ëê1 |
0ûú |
Дана матрица соединений для линии с n узлами. Выяснить, является ли линия уникурсальной, и если является, то получить последовательность номеров узлов, которые будут пройдены во время требуемого вычерчивания.
§18. Сортировка массивов и файлов *)
*) В задачах 628 – 648 этого параграфа существенно, что данные рассматриваются в программе как массив; в задачах 649 – 657 рассматриваются файлы, и это усложняет некоторые алгоритмы.
628. Рассмотрим массив целых или действительных чисел a1,…,an. Пусть требуется представить элементы этого массива так, чтобы после перестановки они были упорядочены по неубыванию: a1≤ a2≤ …≤ an. Эта задача называется задачей сортировки или упорядочения массива (эту же задачу можно рассматривать применительно к упорядочению по невозрастанию: a1≥ a2≥ …≥ an; если числа попарно различны, то можно говорить об убывании и о возрастании). Для решения этой задачи можно воспользоваться, например, следующими алгоритмами:
а) Найти элемент массива, имеющий наименьшее значение, переставить его с первым элементом, затем проделать то же самое, начав со второго элемента и т.д. (Сортировка выбором.)
б) Последовательным просмотром чисел a1, …, an найти наименьшее i такое, что ai>ai+1. Поменять местами ai и ai+1, возобновить просмотр с элемента ai+1 и т.д. Тем самым наибольшее число передвинется на последнее место. Следующие просмотры начинать опять сначала, уменьшая на единицу количество просматриваемых элементов. Массив будет упорядочен после просмотра, в котором участвовали только первый и второй элементы.(Сортировка обменами.)
в) Просматривать последовательно a2, …, an и каждый новый элемент ai вставлять на подходящее место в уже упорядоченную совокупность a1, …, ai-1. Это место определяется последовательным
сравнением ai с упорядоченными элементами a1, …, ai-1. (Сортировка простыми вставками.)
Написать программы, реализующие алгоритмы а), б), в).
629.Исследовать число сравнений и число перемещений (т. е. перестановок с одного места на другое) элементов a1, …, an в процессе применения описанных в предыдущей задаче алгоритмов. Показать, что число перемещений для алгоритма сортировки выбором ограничено некоторой линейной функцией от n. В это же время и число сравнений для алгоритма сортировки выбором, и обе указанные характеристики для алгоритмов сортировки обменами и сортировки простыми вставками в некоторых случаях (например, когда исходный массив таков, что a1>a2>…>an) являются квадратичными функциями от n.
630.Из утверждения предыдущей задачи следует, что алгоритм сортировки выбором выгодно отличается от алгоритмов сортировки
