Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию [pdf]

§12. Использование процедур*)

*) В задачах этого параграфа будем для краткости говорить просто о процедурах, подразумевая, что решающий задачи сам выберет подходящее средство программирования – подпрограмму, функцию и т. д. Этот выбор должен быть сделан с учётом как характера задач, так и особенностей используемого языка программирования.

424. Даны действительные числа s, t. Получить f(t, –2s, 1.17)+f (2.2, t, s – t),

где

425. Даны действительные числа s, t. Получить g(1.2, s)+g(t, s)–g(2s–1, st),

где

427. Даны действительные числа а, b, с. Получить

428.Даны действительные числа a, b. Получить

u = min(a,b),υ = min(ab, a + b), min(u + υ 2 , 3.14).

429.Даны натуральные числа n, m, целые числа a1, ..., an, b1, ..., bm, c1, ..., c30. Получить

430. Даны натуральные числа k, l, m, действительные числа

x1 , ..., xk , y1 , ..., yl , z1 , ..., zm . Получить

432. Даны действительные числа a0, ..., a6. Получить для x=1, 3, 4 значения p(x+1) – p(x), где

p(y)=a6 y6+a5 y5+...+a0.

433. Даны действительные числа s, t, a0, ..., a12 . Получить p(1) – p(t)+p2(s – t) – p3(1),

где

p(x) = a12 x12+a11x11+ ... +a0.

434.Даны действительные числа a1, ..., an, b1, ..., bm. В последовательности a1,...,an и в последовательности b1,...,bm все члены, следующие за членом с наибольшим значением (за первым по порядку, если их несколько), заменить на 0.5.

435.Даны целые числа a1, ..., an, b1, ..., bm, k. Если в последовательности a1, ..., an нет ни одного члена со значением k, то

первый по порядку член этой последовательности, не меньший всех остальных членов, заменить на значение k. По такому же правилу

преобразовать последовательность b1, ..., bm применительно к значению 10.

436. Даны целые числа n0, d0, n1, d1, ..., n7, d7, a, b (d0d1...d7b ≠ 0.

процедуры полного сокращения рационального числа, заданного числителем и знаменателем, а также процедуры сложения и умножения рациональных чисел.

437. Даны целые числа f0, ..., f10. Исследовать существование целочисленных корней уравнения f10x10 + f9x9 + ... + f0=0. (Если f0 = 0, то имеется корень 0; если же f0 ≠ 0, то целочисленный корень, если он существует, принадлежит конечному множеству положительных и отрицательных делителей числа f0.) Здесь полезно определить процедуру вычисления по схеме Горнера значения многочлена, а также процедуру, которая по двум заданным числам k и m (m > k ≥ 0)

позволяет определить значение наименьшего делителя числа m, содержащегося среди чисел k+1, k+2, ..., m.

438. Даны натуральное число n, действительные числа x, y, an, bn, an-1, bn -1, ..., a0, b0. Вычислить по схеме Горнера значение многочлена с комплексными коэффициентами

(an + ibn )(x + iy)n + (an− 1 + ibn− 1)(x + iy)n− 1 + ... + (a0 + ib0 ) . (Определить процедуры выполнения арифметических операций над комплексными числами.)

439.Даны действительные числа u1, u2, v1, v2, w1, w2. Получить

iw2. (Определить процедуры выполнения арифметических операций над комплексными числами.)

440.Даны натуральное число n, целые числа a1, ..., an. Рассмотреть отрезки последовательности a1, ..., an (подпоследовательности идущих подряд членов), состоящие из

а) полных квадратов; б) степени пятёрки; в) простых чисел.

В каждом случае получить наибольшую из длин рассматриваемых отрезков. (Определить процедуры, позволяющие распознавать полные квадраты, степени пятёрки, простые числа.)

441.Дано натуральное число n. Среди чисел 1,2, ..., n найти все те, которые можно представить в виде суммы квадратов двух натуральных чисел. (Определить процедуру, позволяющую распознавать полные квадраты.)

442.Даны действительные числа x1, y1, x2, y2, ..., x10, y10. Найти периметр десятиугольника, вершины которого имеют соответственно

координаты (x1, y1), (x2, y2), ..., (x10, y10). (Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами.)

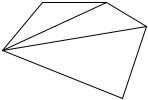
443. Даны действительные числа a, b, c, d. Найти площадь пятиугольника, изображенного на рис. 18. (Определить процедуру вычисления площади треугольника по трем его сторонам.)

a

b

1 2 2,5

c

d

Рис. 18

444. Даны натуральное число n, действительные числа x1, y1, x2, y2, ..., xn, yn. Найти площадь n– угольника, вершины которого при некотором последовательном обходе имеют координаты (x1, y1), (x2, y2),

..., (xn, yn). (Определить процедуру вычисления площади треугольника по координатам его вершин.)

445.Дано четное число n > 2; проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная) заключается в том, что каждое четное n, большее двух, представляется в виде суммы двух простых чисел. (Определить процедуру, позволяющую распознавать простые числа.)

446.Дано натуральное число n. Выяснить, имеются ли среди чисел n, n+1, ..., 2n близнецы, т.е. простые числа, разность между которыми равна двум. (Определить процедуру, позволяющую распознавать простые числа.)

447.Даны натуральное число n, целые числа a1, ..., an. Рассмотреть все отрезки последовательности a1, ..., an (см. задачу 440),

состоящие из совершенных чисел. (Определить процедуру, позволяющую распознавать совершенные числа.)

448. Бесконечная последовательность рациональных чисел v0, v1, ... образована по следующему закону:

Дано неотрицательное целое число n. Вычислить числитель и знаменатель несократимой формы числа vn. (Определить процедуры полного сокращения рационального числа, заданного числителем и знаменателем, а также процедуры сложения и умножения рациональных чисел.)