27. Размах, мода и медиана выборки.

Опр: Модой выборки называется значение варианты или признака, которому соответствует максимальная частота.

Опр: Медианой выборки называется значение признака , которое разделяет всю выборку на 2 половины.

Опр: Промежуток x_набл = [x₁- x_(n)] = [x_{min_набл} - x_{max_набл}] между крайними членами вариационного ряда называется интервалом варьирования, его длина W_n = x_(n) - x₍₁₎ = x_{max_набл} - x_{min_набл} называется размахом выборки.

28. Полигон и кумулята. Графический способ нахождения моды интервального вариационного ряда.

Полигон – график по оси х – признак х_j, по оси у – частота m_j (в случае непрерывного признака гистограмма).

Кумулята - график (х_j, S_j)

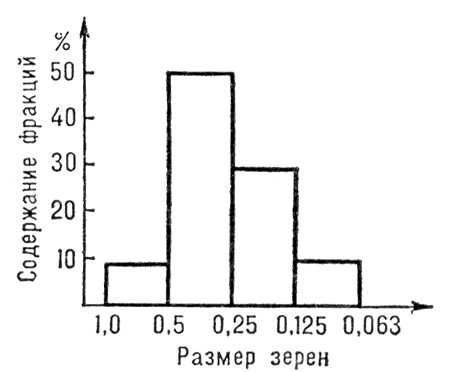
Гистограмма – график по оси х – ширина интервала, по оси у – частота интервала. Мо (мода) для интервала вар. ряда

29. Коэффициент концентрации Джини и кривая Лоренца.

Если в вариационном ряду присутствуют 2 связаных между собой показателя, то между суммарными данными по этим показателям существует связь, которая графически изображается кривой Лоренца.

Пр: обеспеченность москвичей городскими такси, доходом населения.

q_i 1

Кривая Лоренца

Отклонение от диагонали

S₁ характеризует неравномерность распределения

S₂ (напр. неравенство доходов населения)

0 p_i

Коэффициент Джини: G = S₁ = 2S₁ = 2 (1/2 – S₂) = 1 – 2S₂

S₁+S₂

G=0распределение пропорциональное, переноса нет.

G=1максимум нервномер. распределение.

G не может быть >1

Коэффициент G считается приближено по формуле:

G ≈ ∑p_iq_i+1 - ∑p_i+1q_i

30. Точечные и интервальные оценки параметров генеральной совокупности. Какая оценка параметра генеральной совокупности называется несмещенной, состоятельной (на примере мо)?

1.Точечной называют оценку, которая определяется одним числом (при малой выборке приводит к грубой ошибке).

Опр: Точечной оценкой Р параметра Р ГС наз. число, которое:

а) определяется выборочной совокупностью по заданному правилу по ф-ле

б) обладает св-вами несмещенности, состоятельности, эффективности и др.

Р – СВ, Р – не явл. СВ.

Опр: Оценка называется несмещенной, если М (р – р) = 0 Мр = р

Опр: Оценка р называется состоятельной, если limn→+∞p-p=0

Опр: Оценка р называется эффективной в классе других оценок р, если

D(p – p) ≤ D(p - p)

2.Интервальной оценкой называют оценку, которая определяется двумя числами – концами интервала (позволяют установить точность и надежность оценок).

Интервальная оценка:

* Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность 𝜰, с которой осуществляется неравенство IΘ - Θ*I < 𝛿, 𝛿 – хар-ет точность оценки. Обычно надежность задается наперёд, берут 𝜰 = 0,95; 0,99; 0,999.

0≤𝜰≤1

* Построение доверительного интервала. Интервальная оценка генеральной средней при известной дисперсии ² ГС

x - t_{𝜰 σn ≤ μ ≤} x + t_{𝜰 * σn} доверительный интервал для ген. совокупности _μ с надежностью 𝜰.

3. Пусть Θ* - статистическая оценка неизвестного параметра Θ теоретического распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема п и вычислим для каждой из них оценку параметра Θ:  Тогда оценку Θ* можно рассматривать как случайную величину, принимающую возможные значения  Если математическое ожидание Θ* не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические ошибки одного знака (с избытком, если М( Θ*) >Θ, и с недостатком, если М(Θ*) < Θ). Следовательно, необходимым условием отсутствия систематических ошибок является требование М(Θ*) = Θ.

Статистическая оценка Θ* называется несмещенной, если ее математическое ожидание равно оцениваемому параметру Θ при любом объеме выборки: М(Θ*) = Θ.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.