- •1) Перестановки, размещения, сочетания
- •2) «37»Векторное произведение
- •1)«31» Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между двумя прямыми
- •2) «101» Числовой ряд.
- •3) «59» Производная сложной функции. Производная обратной функции
- •1)«27» Прямая, как линия первого порядка. Общее уравнение прямой.
- •2) «66» Основные теоремы о дифференцируемых функциях: Ферма, Ролля, Лагранжа, Коши
- •3) «102» Сумма ряда, необходимый признак сходимости
- •1) «10» Миноры. Теорема о разложении. Алгебраические дополнения
- •2) «68» Формула Тейлора. Разложение элементарных функций. Формула Маклорена
- •3) «85» Определенный интеграл с переменным верхним пределом. Формула Ньютона — Лейбница
- •1) «30» Точка пересечения двух прямых
- •2) «63» Дифференциал функции. Геометрический смысл дифференциала
- •1)21. Линейная независимость системы векторов.
- •2) «71»Достаточное условие экстремума функции в точке.
- •3) «90» Предел функции нескольких переменных, частное и полное приращение функции, непрерывность функции
- •2)«72» Выпуклость графика функции. Достаточное условие выпуклости графика функции.
- •2) «53» Классификация точек разрыва
- •1. Устранимый разрыв.
- •3) «107» Знакопеременные ряды. Абсолютная и условная сходимость
- •2) «69» Монотонность функции. Признак монотонности
- •3) 99» Понятие двойного интеграла. Двойной интеграл в прямоугольных декартовых координатах
- •2) «76» Понятие первообразной и неопределенного интегралa
- •3) «117» Теорема о структуре общего решения линейного однородного уравнения высшего порядка
- •Второй замечательный предел
- •2) «98» Необходимые и достаточные условия экстремумов функции нескольких переменных
- •3) «105» Интегральный признак сходимости
- •1) Уравнения прямой в пространстве.
- •1) «51» Бесконечно малые функции. Свойства бесконечно малых функций
- •3) Частные производные 1-го порядка, их геометрический смысл.
- •1) Основные свойства предела функции
- •2) Приложения определенного интеграла (нахождение объема тела вращения, длины дуги, площади поверхности тела вращения в декартовой и полярной системах координат) Вычисление объема тела вращения
- •3)Степенные ряды
- •1) Исследование функций с помощью первой и второй производных. Построение графиков функций по характерным точкам.
- •3) «118» Общее решение линейного неоднородного уравнения высшего порядка
- •Второй замечательный предел
- •2)«74» Асимптоты графика функции (вертикальная, горизонтальная, наклонная
- •3. 113» Линейные уравнения первого порядка. Уравнения Бернулли «114» Уравнения в полных дифференциалах. Теорема Коши
- •1.Полный дифференциал функции нескольких переменных. Производная сложной функции.
- •2.Математическим ожиданием дискретной случайной величины.
- •3. Диаграммы Эйлера-Венна
- •1. Основные свойства матриц. Транспонированная матрица.
2) «101» Числовой ряд.
Пусть
дана послед-сть чисел u1,
u2,u3,…,un,…
, где un
=f(n), -
бесконечная числовая послед-сть.
Выражение u1+ u2 + u3+...+
un
+... наз-ся бесконечным числовым рядом,
а числа u1, u2,u3,…,un…членами
ряда; un=f(n)
– общим членом. Ряд
часто записывают в виде
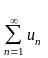
«104» Признаки сходимости д, Аламбера и Коши
Пусть
в положит. ряде u1, u2,u3,…,un,…
отношение
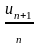 последующего члена к предыдущему при
n
последующего члена к предыдущему при
n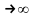 имеет предел q. Возможны
три случая: 1)q<1 тогда
ряд сходится. 2)q>1 тогда
ряд расходится. 3)q=1,тогда
ряд может сходиться, а может и расходиться
(признак Даламбера).
имеет предел q. Возможны
три случая: 1)q<1 тогда
ряд сходится. 2)q>1 тогда
ряд расходится. 3)q=1,тогда
ряд может сходиться, а может и расходиться
(признак Даламбера).
Если
для ряда u1, u2,u3,…,un,…
существует
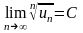 ,
то этот ряд сходится при С<1 и расходится
при С>1. (признак Коши)
,
то этот ряд сходится при С<1 и расходится
при С>1. (признак Коши)
3) «59» Производная сложной функции. Производная обратной функции
Производная сложной функции. y’=f’(x)x’(t)
Обычно
![]() называют внешней функцией, а
называют внешней функцией, а
![]() -
внутренней. При вычислении производной
сложной функции сначала дифференцируют
внешнюю функцию, не обращая внимания
на внутреннюю (ведь она может быть
любой), затем умножают на производную
конкретной внутренней функции.
-
внутренней. При вычислении производной
сложной функции сначала дифференцируют
внешнюю функцию, не обращая внимания
на внутреннюю (ведь она может быть
любой), затем умножают на производную
конкретной внутренней функции.
Производная
обратной функции.![]() .
.
«62» Производные высших порядков
Производной n-го порядка называется производная от производной (n-1)-го порядка.
Обозначение производной f’’(x)-второго порядка, f’’’(x) – третьего порядка.
Для обозначения производных более высокого порядка используют арабские цифры в скобках или римские цифры, например f(4)(x),…. f(n)(x) или fIV(x) и т.д ∆y=f(x+∆x)-f(x)
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда x получает приращение ∆х
Геометрический смысл 2й производной: она является ускорением
Билет №4
«27» Прямая, как линия первого порядка. Общее уравнение прямой.
«66» Основные теоремы о дифференцируемых функциях: Ферма, Ролля, Лагранжа, Коши.
«89» Методы приближенных вычислений определенного интеграла: формула прямоугольников, формула трапеций, формула Симпсона.
Представить комплексное число в тригонометрической форме
1)«27» Прямая, как линия первого порядка. Общее уравнение прямой.
Уравнение ax + bу + c = 0 – уравнение первого порядка, если хотя бы один из коэффициентов a и b не равен нулю. ax + bу + c = 0 – общее уравнение прямой.
2) «66» Основные теоремы о дифференцируемых функциях: Ферма, Ролля, Лагранжа, Коши
Теорема Ферма. Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функции, то производная функции в этой точке = 0, т.е. f’(x0)=0
Геометрический смысл: в точке наибольшего или наименьшего значения, достигаемого внутри промежутка Х, касательная к графику функции параллельна оси абсцисс.
Теорема Ролля. Пусть функция y=f(x) удовлетворяет условиям: непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), на концах отрезков принимает равные значения, т.е. f(a)=f(b). Тогда внутри отрезка по крайней мере существует хотя бы одна такая точка ξ принадлежит (a;b), в которой производная функции =0, т.е. f”(ξ)=0
Геометрический смысл: найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс, в этой точке производная и будет равна 0.
Теорема Лагранджа. Пусть функция
y=f(x)
удовлетворяет условиям: непрерывна на
отрезке [a;b],
дифференцируема на интервале (a;b).
Тогда внутри отрезка существует по
крайней мере одна такая точка ξ
принадлежащая (a;b),
в которой производная равна частному
от деления приращения функции на
приращение аргумента на этом отрезке,
т.е.
![]()
Следствие: если производная функции y=f(x) равна 0 на некотором промежутке Х, то функция тождественно постоянна на этом промежутке.
Теорема Коши. Если функции f(x) и
g(x) непрерывны на отрезке [a, b] и
дифференцируемы на интервале (a, b) и
g¢(x) ¹ 0 на интервале (a, b), то существует
по крайней мере одна точка e, a < e < b,
такая, что![]()
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке e.
«89» Методы приближенных вычислений определенного интеграла: формула прямоугольников, формула трапеций, формула Симпсона
Суть приближенного вычисления определенных интегралов.
Так как в геометрическом смысле значение определенного интеграла есть площадь подграфика подынтегральной функции, то приближенное вычисление сводится к приближенному представлению площади подграфика в виде набора прямоугольников (в методе прямоугольников), трапеций (в методе трапеций) или ограниченных сверху параболами сегментов (в методе Симпсона).
М
прямоугольников.![]() М трапеций.
М трапеций.
![]() М
парабол (метод Симпсона).
М
парабол (метод Симпсона).
![]()
Алгоритм действий.
Сначала разбиваем отрезок [a;b] интегрирования на n частей ( 2n частей для метода Симпсона или метода средних прямоугольников). Это делается по формуле
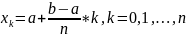 для методов левых, правых прямоугольников
и трапеций и по формуле
для методов левых, правых прямоугольников
и трапеций и по формуле
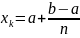 *k, k=0,1,…,2n-
для метода средних прямоугольников и
метода Симпсона.
*k, k=0,1,…,2n-
для метода средних прямоугольников и
метода Симпсона.Вычисляем значения подынтегральной функции в нужных точках . f(xk)
Используем соответствующую формулу.
Для метода левых прямоугольников .
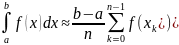
Для метода средних прямоугольников .
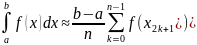
Для метода правых прямоугольников .
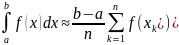
Для метода трапеций

. Для метода парабол (Симпсона)
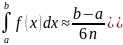 .
.
Билет №5
«15» Решение системы линейных уравнений АХ=В в матричной форме.
«17» Теорема Крамера.
«84» Определенный интеграл: определение, свойства, геометрический смысл.
«102» Сумма ряда, необходимый признак сходимости.
Решить дифференциальное уравнение
1) «15» Решение системы линейных уравнений АХ=В в матричной форме.
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x1 , x2 , ..., xn:
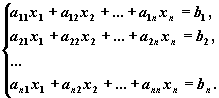 Эта
система в "свернутом" виде может
быть записана так: S ni=1aij
xj = bi , i=1,2,
..., n.
Эта
система в "свернутом" виде может
быть записана так: S ni=1aij
xj = bi , i=1,2,
..., n.
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где
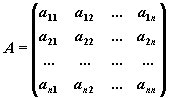 ,
,
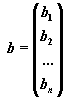 ,
,
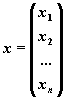 .
.
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.
Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.
Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой:
x=A -1 b.
Справедливо следующее утверждение (формулы Крамера).
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1 , x2 , ..., xn, определяемое формулами Крамера
xi =Di / D, i=1,2, ..., n,
где Di - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b
«17» Теорема Крамера
Если в системе линейных уравнений |A|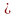 0,
то имеется единственное решение, которое
находим по формулам: xi=
0,
то имеется единственное решение, которое
находим по формулам: xi=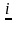 ,
i=1,2,3, где i-
того столбца на столбец свободных
членов.
,
i=1,2,3, где i-
того столбца на столбец свободных
членов.
Решение по этим формулам называется решением по правилу Крамера, или в матричной форме: Х=А-1*В.
2) «84» Определенный интеграл: определение, свойства, геометрический смысл
Определение: Пусть дана функция , которая определена на отрезке. Если существует предел, не зависящий отспособа разбиения отрезка и выбора точек, то такой предел называется определенным интегралом функции.
Геометрический
смысл: Определённый
интеграл
![]() представляет
собой площадь криволинейной трапеции,
ограниченной линиями y
= 0, x
= a,
x
= b,
y
= f(x)
(см. рис. 5.).
представляет
собой площадь криволинейной трапеции,
ограниченной линиями y
= 0, x
= a,
x
= b,
y
= f(x)
(см. рис. 5.).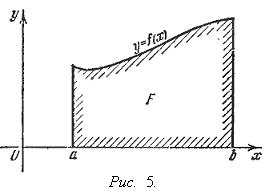
Свойства:
1.
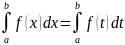 ;
2.
;
2.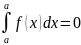 ;
3.
;
3.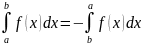 ;
4
;
4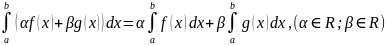 ;
5.
;
5.
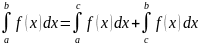 ;
;
6.
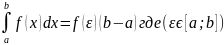 ;
7. Если y=f(x)
– четная
функция, то
;
7. Если y=f(x)
– четная
функция, то
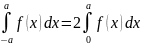 ;
Если y=f(x)
– нечетная,
то
;
Если y=f(x)
– нечетная,
то