Билет №1

1. «3» перестановки, размещения, сочетания

2. «37» Векторное произведение и его основные свойства.

   1. «38» Скалярное произведение и его основные свойства.

3. «131» Случайная величина и ее числовые характеристики.

4. –

1) Перестановки, размещения, сочетания

Вариант упорядочивания данного множества называется перестановкой (permutation). Например, есть множество, состоящее из 3 элементов - А, В, и С. Пример перестановки - СВА. Число всех перестановок из n элементов Пр: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА

Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement)

Пример размещения из 3 по 2: АВ или ВА - это два разных размещения. Число всех размещений из n по m Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ

Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination). Пример сочетания из 3 по 2: АВ. Число всех размещений из n по m

Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ

Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями

2) «37»Векторное произведение

Векторы — величины, для характеристики которых необходимо знать не только их числовые значения, но и направление: F, скорость, ускорение.

О: Векторным произведением векторов в и именуется вектор , который определяется следующим образом:

1) ; 2) ;

3) векторы , , образуют правую тройку (рис. 2.15).

Для векторного произведения используются символы

Рис. 2.15

Свойства векторного произведения:

1⁰. Антипереместительный закон:

□ Векторы и по определению векторного произведения обладают равными длинами, являются коллинеарными, однако направлены в разные стороны, следовательно

2⁰. Сочетательный закон: .

3⁰. Распределительный закон: .

4⁰. Площадь параллелограмма, который построен на векторах и : , а площадь треугольника .

Свойства выводятся из определения векторного произведения.

5⁰. Необходимое и достаточное условие коллинеарности ненулевых векторов и есть то, что их векторное произведение равно нулю.

«38» Скалярное произведение векторов

Ключевые слова: вектор, координаты, скалярное произведение

Определение. Скалярным произведением векторов называется произведение их длин на косинус угла между ними

Утверждения:

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.

Скалярное произведение двух векторов − a(a1;a2;a3)   и − b(b1;b2;b3) ,   заданных своими координатами, может быть вычислено по формуле (− a − b)=a1 b1+a2 b2+a3 b3 .

Основные свойства скалярного произведения

Для любых векторов  − a, − b и − c и любого числа справедливы равенства:

• (− a)2=(− a − b) 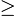0 , причем  (− a)2=0 − a=− 0 ;

• переместительный закон: (− a − b)=(− b − a);

• распределительный закон:  (− a+− b − c)=(− a − c)+(− b − c);

• сочетательный закон: (− a − b)=( − a − b).

3) «131» Случайная величина. Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения.

Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин.

Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:

Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания: D[Х]=M[X-M(X)]²

Моментом k-порядка называется математическое ожидание k-й степени отклонения случайной величины Х от некоторой постоянной с.

Если в качестве с берется нуль, моменты называются начальными ν_k = М(Х)^k

Если с = М(Х), то моменты называются центральными μ = M[X – M(X)]^k

Билет 2

1. «31» Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между двумя прямыми

2. «32». Эллипс. Определение. Вывод канонического уравнения

3. Скалярное произведение векторов