6. Системы линейных уравнений. Основные понятия и определения.

a_ij – коэффициенты при неизвестном

b_i – свободные члены.

i/j от 1 до n

Решением данной системы называется упорядоченная совокупность n чисел: c₁, c₂, c₃…c_n, подстановка которых в каждое уравнение системы обращает его в истинное тождество.

Система, имеющая хотя бы одно решение, называется совместной.

Система, не имеющая ни одного решения, называется не совместной.

Совместная система называется определённой, если она имеет только одно решение и не определённой, если она имеет более одного решения.

Линейная система называется не определённой, если существуют свободные члены, отличные от нуля.

Если все свободные члены равны нулю, то такая система называется однородной.

Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений.

Любые две не совместные системы всегда эквивалентны (нет решений).

7. Решение систем линейных уравнений методом обратной матрицы и методом Крамера:

Формула решения системы методом обратной матрицы:

X = A^-1*B, применяется если определитель прямой матрицы отличен от нуля.

Где Х – матрица столбец, содержащая решения системы x₁, x₂…x_n, а В – матрица столбец, в которой содержатся свободные члены системы b₁, b₂…b_n.

Рассмотрим квадратную матрицу

  .

Обозначим  =det A. – определитель.

Обратная матрица вычисляется по формуле

где А _{i j} - алгебраические дополнения элементов a _{i j}.

А_ij = (-1)^i+j * М_ij

Рассмотрим систему уравнений, решив её методом Крамера:

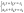
Вычислим определитель:

,

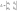Если , то система имеет бесконечно много решений или несовместна (не имеет решений).

В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

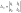Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:   и

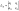
Корни уравнения находим по формулам: ,

8. Решение систем линейных уравнений методом Гаусса и с использованием преобразований Жордана-Гаусса:

Для решения данной системы применяется метод последовательного исключения неизвестных (метод Гаусса) с использованием жордановских преобразований. Такой совокупный метод носит название метода Жордана-Гаусса. Для этого метода удобно записывать систему таблицей.

Выбираем любой не нулевой элемент таблицы (в качестве выбранного элемента должен быть коэффициент при переменной) a_ij. Свободные члены никогда не выбираются. Выбранный коэффициент заключается в прямоугольную рамочку (этот элемент называется разрешающим). Строка и столбец, содержащие данный элемент также называются разрешающими или разрешёнными

Система уравнений называется разрешённой, если каждое уравнение системы содержит разрешённую неизвестную. Разрешённые неизвестные взятые по одной из каждых уравнений, образует полный набор разрешённых неизвестных систем. Разрешённые неизвестные, входящие в полный набор также называются базисными, а все остальные свободными.

Для того, чтобы провести Жордана-Гауссовские преобразования, нужно разрешающую строку умножить на подходящий коэффициент и сложить полученную строку с другой (желательно, чтобы коэффициент был противоположным разрешающему элементу, либо любым другим числом, при сложении с которым получался бы нуль).

Таким образом проделываем вышесказанное с каждой строкой и получаем упрощённый вариант нашей системы, из которой уже можно получить решения заданной системы уравнений.