3 Написать формулу кардиолипина и написать их хар-ку

Кардиолипин. Своеобразным представителем глицерофосфолипидов явл кардиолипин, впервые выделен из сердечной мышцы. По своей хим стр-ре кардиолипин можно рассм-ть как соед-ние, в к-ром 2 мол-лы фосфатидной к-ты связаны с помощью одной мол-лы глицерина. В отличие от остальных глицерофосфолипидов кар-диолипин явл как бы «двойным» глицерофосфолипидом. Кардио-липин локализован во внутренней мембране митохондрий. Функция его пока неясна, хотя известно, что в отличие от других фосфолипидов кардиолипин обладает иммунными св-вами.

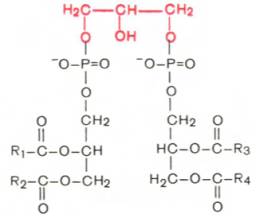
Кардиолипин

4 Кинетика фер-тативных процессов ур-ние михаэлис-Мэнтен

Общие принципы кинетики хим р-ций применимы и к ф-тативным р-циям. Известно, что любая хим р-ция хар-ризуется константой термодинамич равновесия. Она выражает состояние химического равновесия, достигаемого системой, и обозначается К_р. Так, для р-ции:

константа равновесия равна произведению конц-ций образующихся в-в, деленному на произведение конц-ции исходных в-в. Значение константы равновесия обычно нах из соотнош констант скоростей прямой (k₊₁) и обратной (k_{– 1} ) р-ций, т.е. К_p = k₊₁/k_–1. В состоянии равновесия скорость прямой р-ции: v₊₁ = k _{+ 1}[ А ] • [ B ] равна скорости обратной р-ции: v_–1 = k _{– 1} [ С ] • [ D ] , т. е. v₊₁ = v_–1 соотв-енно k₊₁[А]•[B] = k_–1[С]•[D], или

Т.об., константа равновесия = отнош констант скоростей прямой и обратной р-ций. Величину, обратную константе равновесия, принято называть субстратной константой, или, в случае ф-тативной р-ции, константой диссоциации ф-т–субстратного комплекса, и обозначать символом K_S. Так, в р-ции

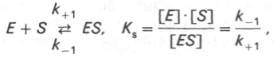
т.е. K_Sравна отношению произведения конц-ции ф-та и субстрата к конц-ции ф-т-субстратного комплекса или отнош констант скоростей обратной и прямой р-ций. Константа K_S зависит от хим природы субстрата и ф-та и определяет степень их сродства. Чем ниже значение K_S, тем выше сродство ф-та к субстрату.

При низкой конц-ции субстрата зависимость скор р-ции от конц-ции субстрата явл почти линейной и подчиняется кинетике первого порядка. Это означает, что скорость р-ции S —> Р прямо пропорц конц-ции субстрата S и в любой момент времени t определяется след кинетическим ур-нием:

где [S] – молярная конц-ция субс-та S; –d[S]/dt – скор убыли субстрата; k' – константа скорости р-ции, к-рая имеет размерность, обратную единице времени (мин^–1 или с^–1).

При высокой конц-ции субстрата скор р-ции максимальна, стан-тся пост и не зависящей от конц-ции субстрата [ S ] . В этом случае р-ция подчиняется кинетике нулевого порядка v = k" (при полном насыщении ф-та субстратом) и целиком определ-ся конц-цией ф-та. Различают р-ции 2-ого порядка, скорость к-рых пропорциональна произведению конц-ций двух реагирующих в-в. В определенных условиях при нарушении пропорциональности говорят иногда о р-циях смешанного порядка.

Изучая явление насыщения, Л. Михаэлис и М. Ментен разработали общую теорию ф-тативной кинетики. Они исходили из предположения, что ф-тативный процесс протекает в виде след хим р-ции:

т.е. ф-т Е вступает во вз-действие с субстратом S с обр-нием промежуточного комплекса ES, к-рый далее распадается на свободный ф-т и продукт р-ции Р. Матем обработка на основе закона действующих масс дала возм-сть вывести ур-ние, названное в честь авторов ур-ем Михаэлиса–Ментен, выражающ кол-ное соотнош м/у конц-цией субстрата и скор ф-тативной р-ции:

где v – скор р-ции при данной конц-ции субстрата [S]; K_S– константа диссоциации ф-т-субстратного комплекса, моль/л; V_max– максим скор р-ции при полном насыщении ф-та субстратом.

Из ур-ния Михаэлиса–Ментен следует, что при высокой конц-ции субстрата и низком значении K_S скор р-ции явл максим, т.е. v = V_max. При низкой конц-ции субстрата, напротив, скорость р-ции оказывается пропорциональной конц-ции субстрата в каждый данный момент (р-ция первого порядка).

Следует указать, что ур-ние Михаэлиса–Ментен в его классическом виде не учитывает влияние на скорость ф-тативного проц продуктов р-ции, напр в р-ции 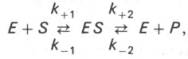и носит несколько ограниченный хар-р. Поэтому были предприняты попытки усовершенствовать его. Так, было предложено ур-ние Бриггса-Холдейна:

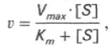где К_m представляет собой константу Михаэлиса, являющуюся экспериментально определяемой величиной. Она может быть представлена следующим ур-нием:

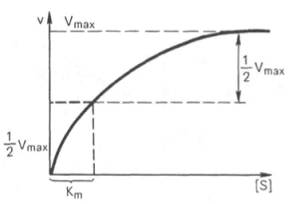Кривая ур-ния Михаэли-са-Ментен: гиперболическая зависимость начальных скоростей катализируемой ф-том р-ции от конц-ции субстрата.

В числителе представлены константы скоростей распада комплекса ES в двух направлениях (в сторону исходных Е и S и в сторону конечных продуктов р-ции Е и Р). Отношение k_–1/ k₊₁представляет собой константу диссоциации ф-тсубстратного комплекса K_S, тогда:

Отсюда вытекает важное следствие: константа Михаэлиса всегда больше константы диссоциации ф-т-субстратного комплекса K_Sна величину k₊₂/k₊₁.

Для определения численного значения К_m обычно находят ту конц-цию субстрата, при к-рой скорость ф-тативной р-ции v составляет половину от максимальной V_max, т.е. если v = ¹/₂ V_maх. Подставляя значение v в ур-ние Бриггса–Холдейна, получаем:

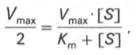
разделив обе части ур-ния на V_mах, получим

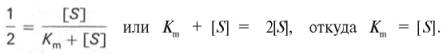
Т.об., константа Михаэлиса численно равна конц-ции субстрата (моль/л), при к-рой скорость данной ф-тативной р-ции составляет половину от максимальной.

Определение величины К_m имеет важное значение при выяснении механизма действия эффекторов на активность ф-тов и т.д. Константу Михаэлиса можно вычислить по графику (рис. 4.13). Отрезок на абсциссе, соотв-ующий скорости, равной половине максимальной, будет представлять собой К_m.

Пользоваться графиком, построенным в прямых координатах зависимости начальной скорости р-ции v₀ от начальной конц-ции субстрата [S₀], неудобно, поскольку максимальная скорость V_maxявл в данном случае асимптотической величиной и определяется недостаточно точно.

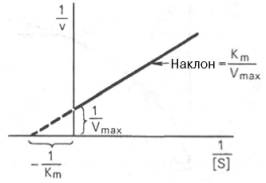График Лайнуивера-Бэрка.

Для более удобного графического представления экспериментальных данных Г. Лайнуивер и Д. Бэрк преобразовали ур-ние Бриггса–Хол-дейна по методу двойных обратных величин исходя из того принципа, что если существует равенство м/у двумя какими-либо величинами, то и обратные величины также будут равны. В частности, ес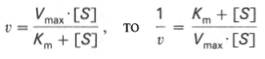ли

или

то после преобр-ния получаем ур-ние:

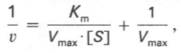
к-рое получило название ур-ния Лайнуивера–Бэрка. Это ур-ние прямой линии: у = ах + b. Если теперь в соотв-ии с этим ур-нием построить график в координатах 1/v (y) от l/[S] (x), то получим прямую линию (рис. 4.14), тангенс угла наклона к-рый будет равен величине K_m/V_max; отрезок, отсекаемый прямой от оси ординат, представляет собой l/V_max(обратная величина максимальной скорости). Если продолжить прямую линию за ось ординат, тогда на абсциссе отсекается отрезок, соотв-ующий обратной величине константы Михаэлиса – 1/К_m (см. рис. 4.14). Т.об., величину К_m можно вычислить из данных наклона прямой и длины отрезка, отсекаемого от оси ординат, или из длины отрезка, отсекаемого от оси абсцисс в области отрицательных значений.

Следует подчеркнуть, что значения V_max, как и величину К_m, более точно, чем по графику, построенному в прямых координатах, можно определить по графику, построенному по методу двойных обратных величин. Поэтому данный метод нашел широкое применение в современной энзимологии. Предложены также аналогичные графические способы определения К_m и V_maxв координатах зависимости v от v/[S] и [S]/v от [S].

Следует отметить нек-рые ограничения применения ур-ния Ми-хаэлиса–Ментен, обусловленные множественными формами ф-тов и аллостерической природой ф-та. В этом случае график зависимости начальной скорости р-ции от конц-ции субстрата (кинетическая кривая) имеет не гиперболическую форму, а сигмоидный хар-р наподобие кривой насыщения гемоглобина кислородом. Это означает, что связывание одной мол-лы субстрата в одном каталитическом центре повышает связывание субстрата с другим центром, т.е. имеет место кооперативное вз-действие, как и в случае присоединения кислорода к 4 субъединицам гемоглобина. Для оценки конц-ции субстрата, при к-рой скорость р-ции составляет половину максимальной, в условиях сигмоидного хар-ра кинетической кривой обычно применяют преобр-нное ур-ние Хилла: