42. Обеспечение достоверности передачи данных с помощью циклических кодов.

Циклические коды являются разновидностью систематических n-разрядных кодов с г-информационными разрядами.

Свойство: если кодовая комбина­ция принадлежит к циклическому коду, то другая комбинация, полученная из первой циклическим сдвигом на один или несколько шагов вправо (вле­во), также принадлежит этому коду.

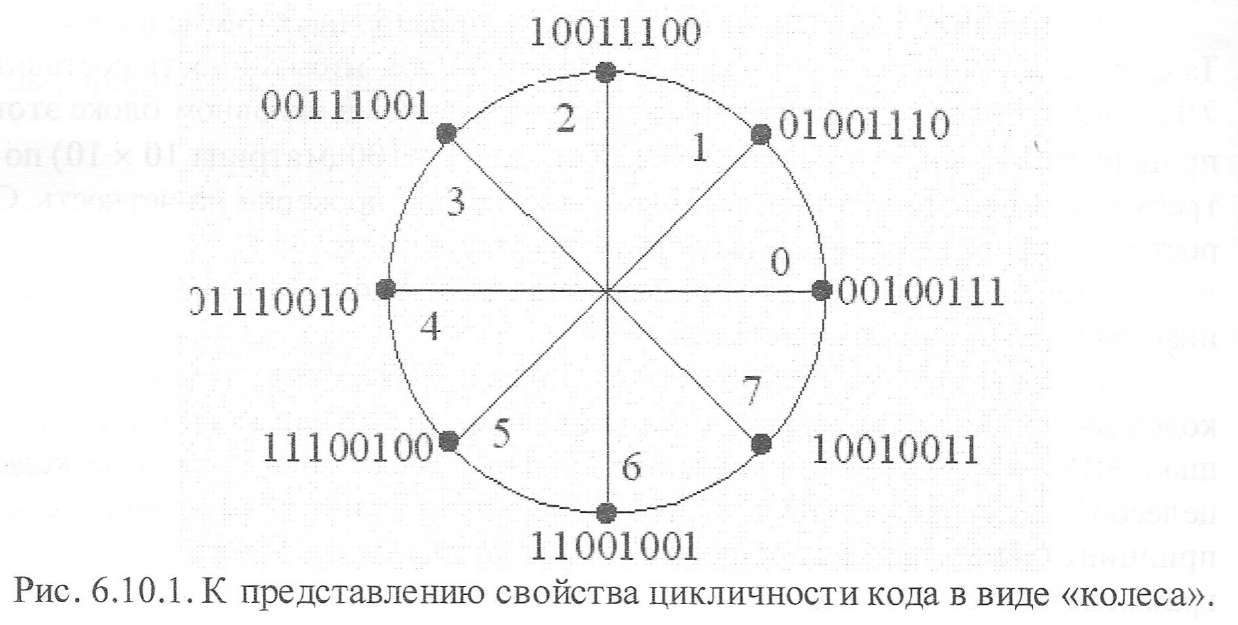
Из этого рисунка видно, что количество «спиц» в таком колесе, рав­ное числу сдвигов комбинации на один разряд, соответствует числу разря­дов в двоичной комбинации.

Для построения циклического кода обозначим через G(x) полином, соответствующий информационной k - разрядной кодовой комбинации, а через F(x) - полином п - разрядного циклического кода. Согласно опреде­лению циклического кода F(x) может быть образован умножением инфор­мационного полинома G(x) на некоторый образующий многочлен Р(х) в степени г:

В данном полиноме F(x) и, следовательно, коде нет четкого разделе­ния позиций информационных и контрольных символов, что усложняет процесс декодирования.

Пример построения циклического кода при k = 7, r = 4.

Пусть задана информационная 11001001, которой соответствует по­лином G(x) = х⁷ + х^б + х³ + 1.

Умножим х G(x), что эквивалентно сдвигу G(x) на 4 разряда влево:

x⁴G(x) = x¹¹ + х¹⁰ + x⁷ +x⁴ Выберем образующий полином (х) = х⁴ + х² + 1. Разделим х⁴G(x) на Р(х):

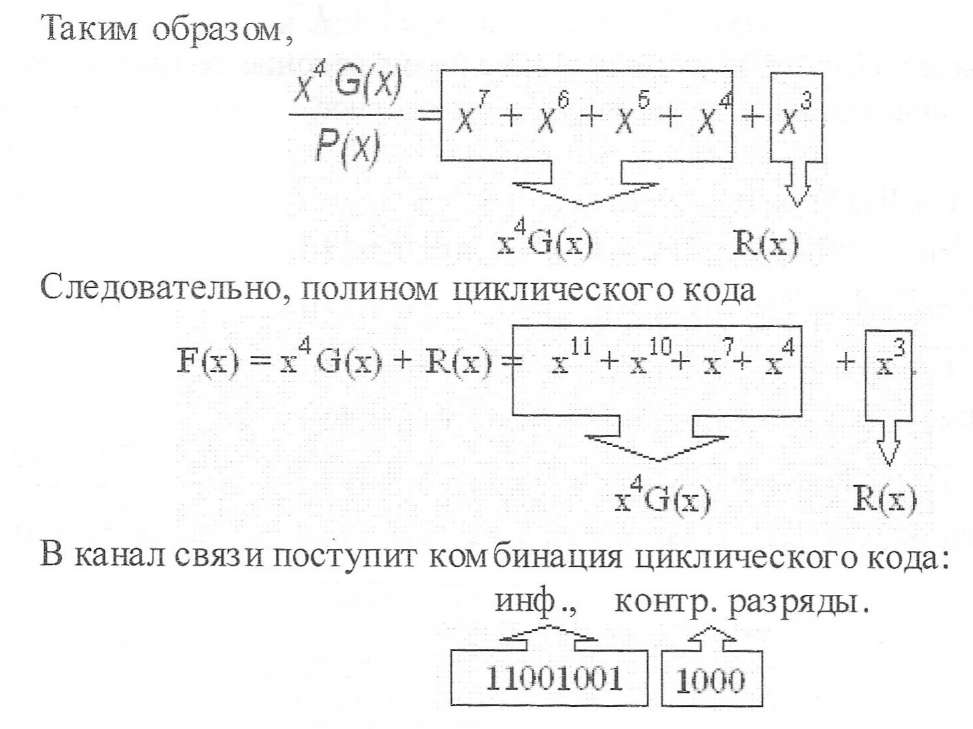
Обнаружение искажений в циклических кодах

Декодирование циклических кодов на приемной стороне сводится к делению принятой комбинации на комбинацию образующего полинома. Если искажения отсутствуют, то деление полинома F(x) на Р(х) будет без остатка.

Под действием помех переданная комбинация, соответствующая по­линому F(x), преобразится в другую, которой будет соответствовать неко­торый полином Н(х).

Математически комбинацию Н(х) можно рассматривать как сумму по mod2 комбинации F(x) и помехи Е(х):

где Е(х) - полином помехи, число слагаемых у которого равно числу искаженных элементов, а степень слагаемых соответствует номеру иска­женного разряда.

При этом деление полинома Н(х) на образующий Р(х) даст ненуле­вой остаток:

Таким образом, основным критерием наличия ошибки в принятом сообщении является неделимость соответствующего ему полинома Н(х) неделимость без остатка на образующий полином Р(х). Если Н(х) делится на Р(х) без остатка, то принятое сообщение рассматривается как неиска­женное, даже если имела место ошибка (случай необнаруженной ошибки).

Основной задачей, решаемой при построении циклического кода, яв­ляется правильный выбор образующего полинома Р(х). Его видом полно­стью определяется корректирующая способность циклического кода.

В системах передачи данных согласно рекомендаций UTI (МККТТ)V.29, V.41 для образования проверочной последовательности используется образующий полином Р(х)=х¹⁶+х¹²+х⁵+1. Его кодовая комбинация 1001000000100001 используется для обна­ружения искажений длиной до 16 бит.

Для построения кодов, обнаруживающих одиночные, двойные и тройные ошибки (d >=4), выбирается образующий полином вида Р(х)=(х+1)Р'(х), где Р'(х) - образующий полином степени r' для кода с d=3. Длина кодовой комбинации выбирается из условия п = 2^r’ - 1: число контрольных разрядов r= r' + 1.