
- •Основные показатели надёжности невосстанавливаемых и восстанавливаемых изделий. Основные выражения для расчетов этих показателей. Примеры.
- •Модель функционирования изделия. Функции обслуживающего персонала. Влияние окружающей среды.
- •Вероятность безотказной работы, её физический смысл, методы вычисления. Пример. Методы увеличения вероятности безотказной работы.
- •Отказы, их виды и причины. Количественная оценка отказа. Отказы программных средств. Сбои в средствах обработки и передачи данных. Частота отказов.
- •Средняя наработка до отказа, её физический смысл, методы расчёта. Пример. Методы увеличения средней наработки до отказа.
- •Наработка на отказ, её физический смысл, методы расчета для изделий, содержащих восстанавливаемые звенья. Пример.
- •Среднее время восстановления, его физический смысл, методы расчёта для изделий, содержащих восстанавливаемые звенья. Пример.
- •Потоки отказов, их общая характеристика. Простейший поток отказов, его модель.
- •Нестационарный Пуассоновский поток отказов, его модель.
- •Комплексные показатели надёжности, их смысл и применимость для оценки надёжности восстанавливаемых изделий и систем.
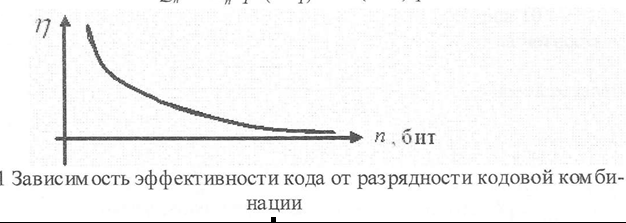
- •Эффективность автоматизированной системы. Основные показатели эффективности, их связь с надёжностью систем.
- •Основные факторы, определяющие надёжность ас. Связь эксплуатационных затрат с затратами на обеспечение надёжности.
- •Общие рекомендации по повышению надёжности средств управления на этапах проектирования. Примеры.
- •Общие рекомендации по конструированию надёжных ктс ас. Учёт требований эргономики.
- •Экономическая оценка повышения надёжности проектируемой ас.
- •Схемотехнические методы повышения надёжности проектируемых систем.
- •Проектная оценка надёжности ктс ас.
- •Виды резервирования, применяемые для повышения надёжности.
- •Виды структурного резервирования и их применимость.
- •Общий нагруженный резерв, оценка его эффективности, применимость в ас. Пример.
- •Общий ненагруженный резерв, оценка его эффективности, применимость в условиях нормальной эксплуатации.
- •Раздельный нагруженный резерв, оценка его эффективности, применимость в ас.
- •Раздельный ненагруженный резерв, оценка его эффективности, применимость в ас.
- •Отказоустойчивые структуры аппаратно-программных средств, оценка их эффективности.
- •Применение принципа голосования для повышения достоверности передачи и обработки данных. Оценка эффективности мажоритарных схем. Методы реализации схем 2 из 3-х.
- •Адаптивные системы голосования, выбор весовых коэффициентов.
- •Методы защиты элементов от обрывов и коротких замыканий, Оценка эффективности защиты.
- •Оптимизация резервирования. Способы включения ненагруженного резерва.
- •Способы включения ненагруженного резерва
- •Оценка надёжности резервируемых восстанавливаемых систем методами теории массового обслуживания. Пример.
- •Структура человеко-машинной системы и оценка влияния человека на надёжность её работы. Основные причины снижения надёжности системы, вызываемые человеком.
- •Анализ влияния человека на надёжность ас
- •Основы эргономического обеспечения ас. Методы обеспечения надёжности работы человека в ас на основе рекомендаций эргономики и инженерной психологии.
- •Концептуальная модель открытой ас. Факторы, определяющие надёжную работу ас и основные рекомендации для повышения надёжности работы человека в открытой системе.
- •Методы обеспечения надёжной работы оператора ас при работе со средствами ввода и отображения информации.
- •Оценка принятия управленческого решения в управляющей системе при наличии экспертов.
- •Обеспечение достоверности хранения и обработки данных с помощью контроля по чётности/ нечётности..
- •Обеспечение достоверности хранения данных на дисковых накопителях с помощью массивов raid.
- •Методы обеспечения достоверности передачи информации по каналам связи.
- •Обнаружение и исправление ошибок в двоичных комбинациях с помощью кода Хэмминга.
- •Обнаружение и исправление ошибок в двоичных комбинациях с помощью матричного кода.
- •Обеспечение достоверности передачи данных с помощью циклических кодов.
- •Основные факторы, определяющие надёжность работы программных средств. Методы обеспечения их надёжности на этапах проектирования и в процессе эксплуатации.
- •Основные рекомендации по повышению надежности пс на этапах разработки
- •Модели надежности программных средств
- •Методы защиты программ при их исполнении.
- •Методы тестирования и диагностики программных и аппаратных средств.
- •Методы контроля и диагностики средств автоматизации.
- •Испытания на надёжность. Виды и программы испытаний. Обработка и представление результатов испытаний на надёжность.
- •1. Основные показатели надёжности невосстанавливаемых и восстанавливаемых изделий. Основные выражения для расчетов этих показателей. Примеры. 1
- •2. Модель функционирования изделия. Функции обслуживающего персонала. Влияние окружающей среды. 1
Обнаружение и исправление ошибок в двоичных комбинациях с помощью матричного кода.
При большой длине кодовой комбинации эффективность кодов с контролем по четности или нечетности низкая, т.к. один контрольный разряд не обеспечивает защиту длинной комбинации.
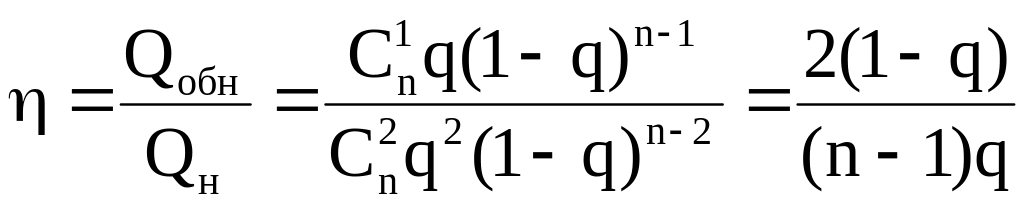
Для увеличения числа контрольных разрядов можно разделить кодовую комбинацию на несколько блоков. В конце каждого блока можно ввести контрольный разряд по четности. Если записать эти блоки в виде матрицы, то можно ввести дополнительные контрольные разряды по столбцам. В результате получится матричный код, относящийся к самокорректирующимся кодам.
Самокорректирующиеся коды характерны тем, что в них закладывается информация о том, как можно восстановить код, если случайные помехи изменят его.
Предположим, что код состоит из отдельных блоков, и в каждом блоке содержится k двоичных символов: а1, а2, ..., ак.
Для работы в канале с переспросом этот код дополняется одним символом - четностью b, выражаемым через символ блока так:
b=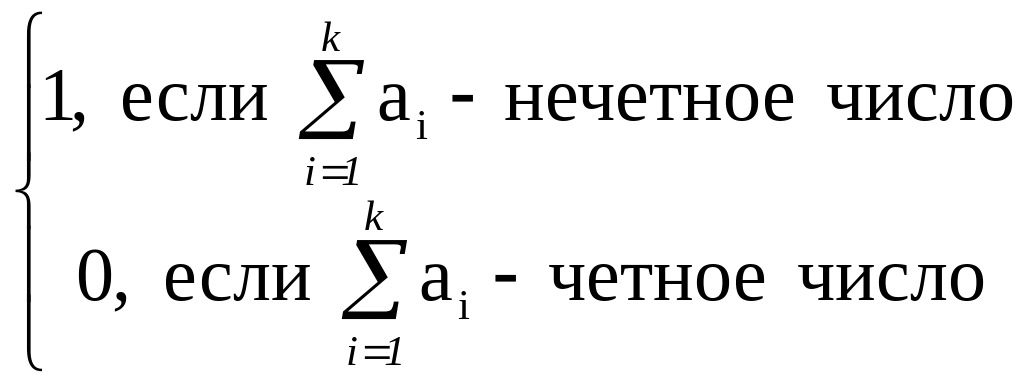
При этом новый блок записывается так: а1, а2, ..., ак,b
Контроль по четности позволяет обнаружить нечетное число ошибок в блоке. Для ответа на вопрос, в каком разряде расположена ошибка, необходимо остановить передачу сообщения и сделать переспрос. Однако, обнаружить и исправить ошибку можно без операции переспроса. Для создания кода с возможностью исправления без переспроса по каналу обратной связи рассмотрим, например, блок с k = 12: а 1, а2, ..., а 12.
Расположим этот основной блок в виде матрицы:

Теперь определим четность всех строк и всех столбцов этой матрицы, приписав по ее краям символы четности b:

Здесь
b1=![]()
b2=![]()
b7=![]()
Считывая последовательно все строки образованной матрицы, можно получить блоке избыточностью: a1a2a3a4b1a5a6a7a8b2a9a1oana12b3b4 b5b6b7. Например, блок 101101000111 можно записать в матричной форме так:

Эту матрицу можно дополнить символами по четности. Полученный блок с избыточностью будет следующим: 1011101001011111000.
Допустим
теперь, что ошибка появилась в
информационном (основном) блоке
![]() .
Тогда
изменение одного двоичного символа на
обратный приводит к нарушению
четности в строке и столбце, соответствующих
этому символу. По этому нарушению легко
восстановить правильное значение
символа. Для этого достаточно символ,
находящийся на пересечении строки и
столбца с нарушением четности, изменить
на обратный.
.
Тогда
изменение одного двоичного символа на
обратный приводит к нарушению
четности в строке и столбце, соответствующих
этому символу. По этому нарушению легко
восстановить правильное значение
символа. Для этого достаточно символ,
находящийся на пересечении строки и
столбца с нарушением четности, изменить
на обратный.
Если ошибка окажется в символах контроля четности, то нарушится лишь одно условие четности.
Для построения кода с исправлением двух, трех и более ошибок необходимо сделать дополнительную проверку на четность, например, по диагоналям. Вводя такую проверку на четность, можно построить самокорректирующийся код с любой надежностью.
Полученный двумерный итеративный код обладает минимальным кодовым расстоянием, равным длине строки 1. Поэтому он позволяет обнаружить пакет ошибок длиной 1 + 1.
Однако при этом увеличивается число проверочных символов в коде. Так, для k = 12 нужно 7 избыточных символов, т.е. избыточность составит 7/12 = 60%. Однако, с увеличением числа символов в основном блоке этот процент избыточности уменьшается. Так, для k = 100 (матрица 10 х 10) потребуется лишь 20 дополнительных символов для проверки на четность. С ростом & число дополнительных символов уменьшается.
Таким образом, с точки зрения экономности кода удобнее передавать информацию большими блоками.
По сравнению с циклическими кодами избыточность итеративных кодов выше. Но кодирование и декодирование итеративных кодов с помощью ЭВМ проще, чем циклических. Поэтому простые итеративные коды целесообразно применять в системах передачи данных, работающих по принципу коммутации сообщений. Их использование обеспечивает программным путем снижение не обнаруживаемых ошибок в 106раз по сравнению с простым без избыточным кодом. Применение же итеративного кода с кодом Хэмминга позволяет снизить количество не обнаруживаемых ошибок в 10 -10 раз.
