37. Обеспечение достоверности хранения и обработки данных с помощью контроля по чётности/ нечётности..

В зависимости от метода введения избыточности блочные коды можно классифицировать на:

1. Разделимые. В разделимых кодах положения информационных и контрольных символов четко разгра­ничены: информационные разряды размещены в определенных позициях кодовой комбинации. На других позициях размещаются контрольные сим­волы.

1.1. Систематические. Систематическим называют код, в котором на информационных по­зициях размещены элементы информационной комбинации, а на кон­трольных позициях - элементы, каждый из которых получается сложением по модулю 2 определенной комбинации информационных кодовых эле­ментов. Иными словами, это коды, в которых сумма по модулю 2 двух лю­бых разрешенных комбинаций кода дает комбинацию этого же кода. Число контрольных символов в таком коде может быть различным.

1.2. Несисте­матические

2. Неразделимые. В неразделимых кодах элементы кодовой комбинации не разделяют­ся жестко на информационные и контрольные. Таким является, например, телеграфный код МТК-З с постоянным соотношением импульсов разной полярности.

Код с четным числом единиц (или код с контролем по четности) - это блочный код, который строится путем дополнения к — разрядном, двоичному коду a_n-1, ..., a₁, а­₀ одного контрольного разрядов - нуля или единицы. При этом количество единиц в каждой кодовой комбинате: должно быть четным. Количество разрядов кода n = n₀ + 1, Формат комбинации с контролем по четности: , где , если количество двоичных единиц четно, иначе , если количество двоичных единиц нечетное.

Такой код имеет минимальное кодовое расстояние d = 2 и позволяет обнаружить все кодовые комбинации с t = 1 искаженным элементом.Ком­бинации с четным числом единиц позволяют обнаружить нечетное число искаженных элементов .

Избыточность кода с четным числом единиц равна:

Избыточность уменьшается с ростом длины кодовой комбинации.

Эффективность такого кода.

Обозначим через q вероятность искажения бита. Тогда вероятность обнаружения ошибки в принятой комбинации определится суммой вероятностей появления в комбинации не­четного числа единиц t = 1, 3, 5, ... в любых сочетаниях: , где: - число искаженных позиций (разрядов) в комбинации.

Вероятность появления не обнаруживаемых ошибок определится суммой вероятностей появления четного числа единиц t+1 в кодовой комбинации:

, где - число искаженных четных единиц в комбинации.

Если пренебречь малыми значениями тройной, четверной и т.д. оши­бок, то отношение вероятностей не обнаруживаемых и обнаруживаемых ошибок будет равно: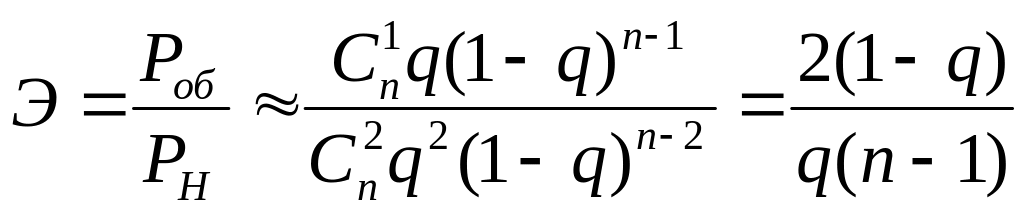

Из этого выражения следует, что с ростом длины информационной комбинации п эффективность кода с контролем по четности уменьшается. Поэтому контроль по четности используется в 1 -байтовых комбинациях.

Для вы­числения контрольного разряда необходимо просуммировать количество единиц в разрядах кодовой комбинации и определить, четное ли их коли­чество. Это состояние является командой для выдачи в проверочный n-й разряд дво­ичной единицы

Операция декодирования также сводится к подсчету числа единиц в принятой кодовой комбинации.

Однако, в каналах связи преобладают групповые ошибки. Для их об­наружения необходимо строить коды с кодовым расстоянием d> 2. Такие систематические коды можно получить, используя производящую и про­верочную матрицы.

Код с контролем по четности (нечетности) позволяет обнаружить одиночную ошибку. В случае ее появления можно образовать команду на повторную операцию, выполняемую контролируемым устройством. Если ошибка сбойная, то при повторной операции она может не появиться. Од­нако определить место возникновения ошибки код с контролем по четно­сти не позволяет.

Для локализации ошибки в кодовой комбинации и ее устранения ис­пользуются матричные коды и коды Хэмминга.