19. Абсолютная и относительная погрешности умножения.

Погрешность произведения: относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел:

d £ d1 + d2 + ... + dn .

Поэтому при вычислении произведения нескольких приближенных чисел применяют следующие правила:

- округляют эти числа так, чтобы каждое из них содержало на одну (или две) значащие цифры больше, чем число верных значащих цифр в наименее точном из сомножителей;

- в результате умножения сохраняют столько значащих цифр, сколько верных цифр имеется в наименее точном из сомножителей.

Пример. Найти произведение х1 = 2.5 и х2 = 72.397 .

Решение. После округления имеем х1=2.5 и х2=72.4 .Т.е. u=x1·x2= 2.5·72.4 = 181 .

20. Метод наименьших квадратов аппроксимации данных: тип метода, принцип метода, степень аппроксимирующего полинома, задача построения полинома, условия и вывод системы уравнений для определения коэффициентов полинома.

При отображении таблично заданной функции y = f(x), i = 0,1, …,n, значения которой получены в результате экспериментов, т.е. содержат ошибки измерений, нет необходимости в точном воспроизведении (интерполировании) значений функции в заданных точках.

Поставим себе задачу отобразить приближëнно функцию y = f(x)

(см. точки на рис. 2.2) полиномом степени m = 2 (параболой) вида:

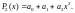(2.31)

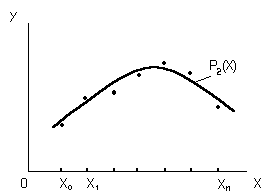
Рис. 2.2

В полиноме (2.31) содержатся три (m + 1) неизвестных коэффи-циентов a₀, a₁, a₂. Определим их из условия

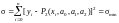, (2.32)

где y_i – результаты измерений функции из экспериментов;

P₂ (x_i, a₀, a₁, a₂) – расчетные значения полинома при x = x_i.

По условию (2.32) требуется, чтобы сумма квадратов отклонений в точках x₀, x₁, …, x_n полинома P₂(x) от функции y = f(x) была минимальной. Это положено в основу метода наименьших квадратов.

Фактически стоит задача найти минимум функции σ = σ(a₀, a₁, a₂). Для еë решения подставим выражение полинома (2.31) в условие (2.32), возьмëм частные производные , , и приравняем их к нулю (условие минимума функции σ). Таким образом, получим систему из трëх уравнений для определения трëх коэффициентов a₀, a₁, a₂ полинома:

После алгебраических преобразований имеем следующую сис-тему уравнений:

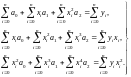(2.33)

Заметим, что .

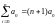Обозначим

Напоминаем, здесь x_i и y_i – значения из таблицы эксперимен-тальных данных.

С использованием введенных обозначений система (2.33) для определения коэффициентов a₀, a₁, a₂ запишется в следующем виде:

(2.33а)

Для решения системы (2.33а), являющейся системой линейных алгебраических уравнений, можно использовать метод Гаусса.

В частном случае, когда данные эксперимента укладываются в плоскости координат x, y вблизи прямой, для их отображения можно взять полином первой степени P₁(x) = a₀ + a₁x, т.е. решить задачу линейной регрессии («регрессия» – обратное движение; в рассмат-риваемой задаче – восстановление выражения функции по отдельным еë значениям).

Система уравнений для определения коэффициентов a₀ и a₁ полинома P₁(x) будет состоять из двух уравнений. С использованием введëнных выше обозначений можем записать:

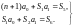(2.34)