§ 7. Сравнение мощностей

Теорема 1 (Кантора-Бернштейна). Пусть для множеств А и В существуют множества А₁ А и В₁ В такие, что множество А равномощно с В₁, а множество В с А₁, то множества А и В равномощны.

Доказательство. Пусть f - биекция В на А₁, а g - биекция А на В₁. Тогда f(В)=А₁ и f(В₁)=А₂ А₁. Суперпозиция h=fog функций является также биекцией А на А₂. Тогда функция h отображает

А на А₂

А₁  А на А₃  А

А₂  А₁ на А₄  А₃

А₃  А₂ на А₅  А₆ и т.д.

Отсюда следует, что h является биекцией

из А – А₁ на А₂ – А₃

из А₁ – А₂ на А₃ – А₄

из А₂ – А₃ на А₄ – А₅ и т.д.

Зададим множества

Е = (А – А₁)(А₂ – А₃)(А₄ – А₅)(А₆ – А₇) ...

F = (А₂ – А₃)(А₄ – А₅)(А₆ – А₇) ...

D = АА₁А₂А₃А₄...

G = (А₁ – А₂)(А₃ – А₄)(А₅ – А₆) ...

Из замеченного выше следует, что h является биекцией E на F. Кроме того, справедливы равенства А = DGE и А = DGF. Следовательно отображение Т из А в А₁, определяемое соотношением

является биекцией А на А₁, т.е. множества А и А₁ равномощны. Последнее означает, что все четыре множества в теореме равномощны.

Теорема 2. Пусть Х и У два множества такие, что Х, У и в У не менее двух элементов. Тогда множество всех функций, действующих из Х в У является множеством, мощность которого больше мощности множества Х.

Доказательство. Обозначим множество функций, действующих из Х в У через У^Х. Доказательство разобьем на две части. Сперва покажем, что существует инъекция множества Х на часть множества У^Х. Пусть у₁У, у₂У, у₁  у₂ и х₀Х. Построим функцию f[х₀] следующим образом: f[х₀](х₀) = у₁, а если х  х₀, то f[х₀] (х) = у₂. При таком построении различным элементам в Х соответствуют различные функции. Например, если х₁  х₀, то f[х₁](х₀) = у₂. Таким образом, получаем инъекцию из Х в У^X.

Покажем теперь, что не существует биекции между Х и У^X. Предположим противное, что g является биекцией из Х на У^X и g(x) = f^x У^Х. Покажем, что существует fУ^Х такое, что f  f^х для любого хХ. Пусть хХ и f^хУ^Х соответствующая функция. Определим f(х) = аУ из условия а  f^х(x). Такой элемент а в У обязательно найдется, т.к. в У не менее двух элементов. Таким образом построенная функция f не будет совпадать ни с одной функцией f . Следовательно g не может быть биекцией.

Теорема 3. Множество всех подмножеств произвольного непустого множества Х имеет мощность большую, чем мощность множества Х.

Доказательство. Положим У={0,1}. Рассмотрим множество У^Х. Если fУ^Х, то f разбивает Х на два множества: Х₀(f) = {xX: f(x)=0} и Х₁(f) = {xX: f(x) = 1}. Таким образом, каждому fУ^X соответствует множество Х₁(f). Наоборот, если Х₁ - некоторое подмножество из Х, то полагая

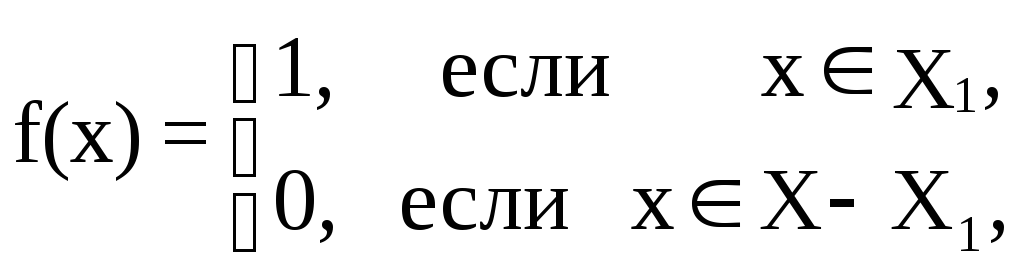
получим fУ^Х. Этим мы построили биекцию между множеством всех подмножеств множества Х и множеством У^Х. Следовательно они равномощны и по теореме 2 мощность множества Х меньше мощности множества всех подмножеств.

Задачи.

1. Пусть А и В произвольные конечные множества, card(А)=n, card(В)=m. Доказать, что общее число отображений из А в В равно n^m.

2. Пусть в условиях предыдущей задачи mn. Определить число биекций и инъекций из А в В.