Метод математической индукции

Во многих разделах математики приходится доказывать истинность утверждения, зависящего от , т.е. истинность высказыванияp(n) для nN (для любого nN p(n) верно).

Часто это удается доказать методом математической индукции.

В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены два условия:

1. Предложение p(n) истинно для n = 1.

2. Из предложения, что p(n) истинно для n = k (k - произвольное натуральное число) следует, что оно истинно для n = k + 1.

Под методом математической индукции понимают следующий способ доказательства

1. Проверяют истинность утверждения для n = 1 – база индукции.

2. Предполагают, что утверждение верно для n = k – индуктивное предположение.

3. Доказывают, что тогда оно верно и для n = k + 1 индуктивный переход.

Иногда предложение p(n) оказывается верным не для всех натуральных n, а начиная с некоторого для n = n₀. В этом случае в базе индукции проверяется истинность p(n) при n = n₀.

Пример 1. Пусть . Доказать, что

1. База индукции: при n = 1 по определению S₁ = 1 и по формуле получаем один результат. Утверждение верно.

2. Индуктивное предположение. Пусть n = k и .

3. Индуктивный переход. Пусть n = k + 1. Докажем, что .

Действительно, в силу индуктивного предположения

Преобразуем это выражение

Индуктивный переход доказан.

Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!

Пример 2. Доказать

.

1. База индукции. При n = 1, утверждение, очевидно, верно.

2. Индуктивное предположение. Пусть n = k и

3. Индуктивный переход. Пусть n = k + 1. Докажем:

Действительно, возведем правую сторону в квадрат как сумму двух чисел:

Используя индуктивное предположение и формулу суммы арифметической прогрессии: , получим

Пример 3. Доказать неравенство

для .

1. Базой индукции в этом случае является проверка истинности утверждения для , т.е. необходимо проверить неравенство. Для этого достаточно возвести неравенство в квадрат:или 63 < 64 – неравенство верно.

2. Пусть неравенство верно для , т.е.

.

3. Пусть , докажем:

.

Используем предположение индукции

Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть

Остается установить, что лишний множитель не превосходит единицы. Действительно,

.

Пример 4. Доказать, что при любом натуральном числооканчивается цифрой.

1. Наименьшее натуральное , с которого справедливо утверждение, равно..

2. Пусть при числооканчивается на. Это означает, что это число можно записать в виде, где– какое-то натуральное число. Тогда.

3. Пусть . Докажем, чтооканчивается на. Используя полученное представление, получим

Последнее число имеет ровно единиц.

Задачи.

1. Доказать, что при каждом верны равенства

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8) .

9) .

10).

2. Доказать, что при любом .

1. кратно .

2. кратно .

3. кратно .

4. кратно .

5. кратно .

6. кратно 19.

3. Доказать справедливость следующих неравенств для всех натуральных .

1. .

2. .

3. .

4. .

5. .

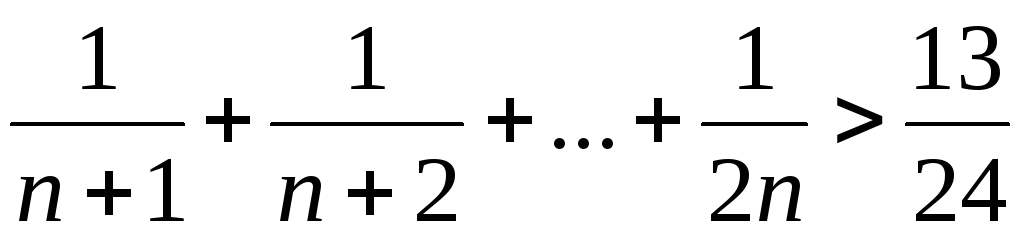4. Доказать, что при любом натуральном верно неравенство

1) . 2).

5. Доказать равенство для любого

1. ,

(в левой части содержится корней).

2. .

6. Пусть – произвольные неотрицательные числа, причем

.

Доказать, что .

7. Доказать неравенство Бернулли

,

8.Пусть – произвольные положительные числа, причем

. Доказать, что .