16. Совместная функция распределения двух случайных величин и её свойства. Совместное распределение двух дискретных случайных величин.

Функцией распределения случайного вектора или совместным распределением случайных величин называется функция, определенная равенством

,

где .

По известной многомерной функции можно найти распределение каждой из компонент .

Например, если - двумерная случайная величина, имеющая совместное распределение , то распределения компонент и вычисляются соответственно по формулам:

, .

В дальнейшем будем рассматривать двумерные случайные векторы.

Случайный вектор называется непрерывным случайным вектором, если существует такая неотрицательная функция , что для любого прямоугольника W  на плоскости вероятность события равна

.

Функция в этом случае называется совместной плотностью распределения.

Легко показать, что .

Если - совместная плотность распределения двумерного случайного вектора , то плотности распределения его компонент определяются равенствам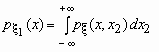и:

и .

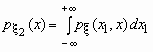Если - дискретный случайный вектор, то совместным распределением случайных величин и чаще всего называют таблицу вида

 

	y1	y2	...	ym
x1	p11	p12	...	p1m
x2	p12	p12	...	p2m
...	...	...	pij	...
xn	pn1	pn2	...	pnm

где и .

По этой таблице можно найти распределения и компонент x и h . Они вычисляются по формулам:

.

17. Абсолютно непрерывные совместные распределения двух случайных величин. Совместная плотность распределения, её свойства.

18. Условные плотности распределения.

Условной плотностью распределения случайной величины x при условии, что случайная величина h принимает значение h = y₀, называется функция переменной x, определяемая формулой

.

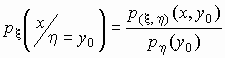Аналогично, условной плотностью распределения случайной величины h при условии, что случайная величина x принимает значение x = x₀, называется функция переменной y, определяемая формулой

.

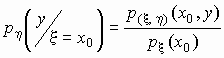19. Распределения n-мерных случайных векторов. Дискретные распределения, абсолютно непрерывные распределения.

Дискретные распределения

Если случайная величина дискретна, то есть её распределение однозначно задаётся функцией вероятности

,

то функция распределения этой случайной величины кусочно-постоянна и может быть записана как:

.

Эта функция непрерывна во всех точках , таких что , и имеет разрыв первого рода в точках .

Абсолютно непрерывные распределения

Распределение называется абсолютно непрерывным, если существует неотрицательная почти всюду (относительно меры Лебега) функция , такая что:

.

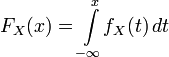Функция называется плотностью распределения. Известно, что функция абсолютно непрерывного распределения непрерывна, и, более того, если , то , и

.

20. Распределение функции от случайной величины. Примеры.