
- •Теория вероятностей.
- •Пространство элементарных исходов.
- •Вероятность на дискретном пространстве элементарных исходов.
- •Классическое определение вероятности
- •Сигма-алгебра событий.
- •Определение вероятности на общем пространстве элементарных исходов. Свойства вероятности.
- •Геометрические вероятности. Примеры.
- •Условная вероятность
- •Независимость событий в совокупности
- •Формула полной вероятности.
- •Последовательность испытаний Бернулли.
- •Теорема Пуассона.
- •Случайные величины. Определение. Функция распределения случайной величины и её свойства.
- •Дискретные случайные величины. Примеры распределения дискретных случайных величин.
- •Абсолютно непрерывные распределения случайных величин. Плотность распределения и её свойства.
- •Примеры абсолютно непрерывных распределений. Равномерное распределение
- •Совместная функция распределения двух случайных величин и её свойства. Совместное распределение двух дискретных случайных величин.
- •Абсолютно непрерывные совместные распределения двух случайных величин. Совместная плотность распределения, её свойства.
- •Условные плотности распределения.
- •Распределения n-мерных случайных векторов. Дискретные распределения, абсолютно непрерывные распределения.
- •Распределение функции от случайной величины. Примеры.
- •Независимость случайных величин.
- •Распределение суммы независимых случайных величин. Формула свертки.
- •Математическое ожидание случайных величин. Свойства математического ожидания. Примеры.
- •Дисперсия случайных величин. Свойства дисперсии. Примеры.
- •Ковариация. Свойства.
- •Коэффициент корреляции. Свойства.
- •Двумерное нормальное распределение и его параметры.
- •Неравенство Маркова. Неравенство Чебышева.
- •Сходимость по вероятности последовательности случайных величин. Свойства сходимости по вероятности.
- •Закон больших чисел.
- •Слабая сходимость последовательности случайных величин и её свойства.
- •Соотношения между слабой сходимостью случайных величин и сходимостью по вероятности.
- •Центральная предельная теорема. Различные формулировки центральной предельной теоремы.
Слабая сходимость последовательности случайных величин и её свойства.
Пусть
задана последовательность случайных
величин
,
задано некоторое распределение
с
функцией
распределения
![]() и
пусть
—
произвольная случайная
величина,
имеющая распределение
.
и
пусть
—
произвольная случайная
величина,
имеющая распределение
.
Определение.
Говорят,
что последовательность случайных
величин
сходится
слабо
или по
распределению
к случайной величине
и
пишут:
![]() ,
если для любого
такого,
что функция распределения
непрерывна
в точке
,
имеет место сходимость
,
если для любого
такого,
что функция распределения
непрерывна
в точке
,
имеет место сходимость
![]() при
.
при
.
Итак, слабая сходимость — это сходимость функций распределения во всех точках непрерывности предельной функции распределения.
Свойства:
Если , и функция распределения непрерывна в точках
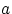 и
,
то
и
,
то
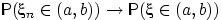 .
Наоборот, если во всех точках
и
непрерывности
функции распределения
имеет
место сходимость
,
то
.
.
Наоборот, если во всех точках
и
непрерывности
функции распределения
имеет
место сходимость
,
то
.Если , то .
Если
 ,
то
.
,
то
.
Соотношения между слабой сходимостью случайных величин и сходимостью по вероятности.
Центральная предельная теорема. Различные формулировки центральной предельной теоремы.
Классическая формулировка Ц.П.Т.
Пусть
![]() есть
бесконечная последовательность
независимых одинаково распределённых
случайных величин, имеющих конечное
математическое
ожидание и дисперсию.
Обозначим последние
есть
бесконечная последовательность
независимых одинаково распределённых
случайных величин, имеющих конечное
математическое
ожидание и дисперсию.
Обозначим последние
![]() и
и
![]() ,
соответственно. Пусть также
,
соответственно. Пусть также
![]() .
.
Тогда
![]() по
распределению при
по
распределению при
![]() ,
,
где
![]() —
нормальное
распределение с нулевым математическим
ожиданием и стандартным
отклонением, равным единице. Обозначив
символом
—
нормальное
распределение с нулевым математическим
ожиданием и стандартным
отклонением, равным единице. Обозначив
символом
![]() выборочное
среднее первых
выборочное
среднее первых
![]() величин,
то есть
величин,
то есть
![]() ,
мы можем переписать результат центральной
предельной теоремы в следующем виде:
,
мы можем переписать результат центральной
предельной теоремы в следующем виде:
![]() по
распределению при
.
по
распределению при
.
Скорость сходимости можно оценить с помощью неравенства Берри-Эссеена.
Замечания
Неформально говоря, классическая центральная предельная теорема утверждает, что сумма независимых одинаково распределённых случайных величин имеет распределение, близкое к
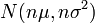 .
Эквивалентно,
имеет
распределение близкое к
.
Эквивалентно,
имеет
распределение близкое к
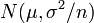 .
.Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив
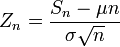 ,
получаем
,
получаем
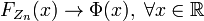 ,
где
,
где
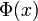 —
функция распределения стандартного
нормального распределения.
—
функция распределения стандартного
нормального распределения.Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).
Вообще говоря, из сходимости функций распределения не вытекает сходимость плотностей. Тем не менее в данном классическом случае имеет место.
Локальная Ц.П.Т.
В
предположениях классической формулировки,
допустим в дополнение, что распределение
случайных величин
![]() абсолютно
непрерывно, то есть оно имеет плотность.
Тогда распределение
абсолютно
непрерывно, то есть оно имеет плотность.
Тогда распределение
![]() также
абсолютно непрерывно, и более того,
также
абсолютно непрерывно, и более того,
![]() при
,
при
,
где
![]() -
плотность случайной величины
,
а в правой части стоит плотность
стандартного нормального распределения.
-
плотность случайной величины
,
а в правой части стоит плотность
стандартного нормального распределения.
Ц.П.Т. Линдеберга
Пусть
независимые случайные величины
определены
на одном и том же вероятностном
пространстве и имеют конечные
математические
ожидания и дисперсии:
![]() .
Как и прежде построим частичные суммы
.
Тогда в частности,
.
Как и прежде построим частичные суммы
.
Тогда в частности,
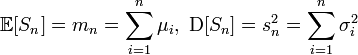 .
Наконец, пусть выполняется условие
Линдеберга:
.
Наконец, пусть выполняется условие
Линдеберга:
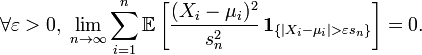
Тогда
![]() по
распределению при
по
распределению при
Ц.П.Т. Ляпунова
Пусть
выполнены базовые предположения Ц.П.Т.
Линдеберга. Пусть случайные величины
![]() имеют
конечный третий
момент. Тогда определена последовательность
имеют
конечный третий
момент. Тогда определена последовательность
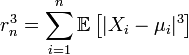 .
Если предел
.
Если предел
![]() (условие
Ляпунова),
(условие
Ляпунова),
то
по распределению при .
Пример. Монета подбрасывается 10000 раз. Оценим вероятность того, что частота выпадения герба отличается от половины на одну сотую или более.
Решение.
Требуется
найти
![]() ,
где
,
где
![]() ,
,
![]() —
число выпадений герба, а
—
число выпадений герба, а
![]() —
независимые
случайные
величины, имеющие одно и то же
распределение
Бернулли с параметром 1/2. Вычислим
вероятность дополнительного
события. Домножим обе части неравенства
под знаком вероятности на
—
независимые
случайные
величины, имеющие одно и то же
распределение
Бернулли с параметром 1/2. Вычислим
вероятность дополнительного
события. Домножим обе части неравенства
под знаком вероятности на
![]() и
поделим на корень из дисперсии
и
поделим на корень из дисперсии
![]() .
.

Искомая вероятность примерно равна 0,0456:
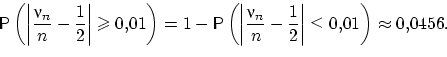
Центральной предельной теоремой пользуются для приближённого вычисления вероятностей, связанных с суммами большого числа независимых и одинаково распределённых величин. При этом распределение центрированной и нормированной суммы заменяют на стандартное нормальное распределение.
Пы. Сы.
Дискретные распределения
Математическое
ожидание случайной величины, которая
может принимать значения x1,
x2,
..., xk
с вероятностями p1,
p2,
..., pk:
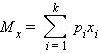
|
Дисперсия
такой величины:
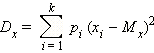
|
Среднеквадратичное
отклонение:
![]()
|
Геометрическое
распределение:
![]()
|
![]()
![]()
|
|
Биномиальное
распределение:
![]()
|
M = N p |
D = N p (1 – p) |
Распределение
Пуассона:
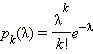
|
M = λ |
D = λ |
Непрерывные распределения
p (dx) = φ (x) dx |
Вероятность
попадания случайной величины в промежуток
[x1; x2]:
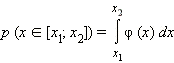
|
Нормировка
плотности вероятности:

|
Математическое
ожидание:
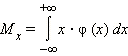
|
Дисперсия:
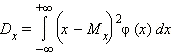
|
Постоянное
распределение:
![]()
![]()
|
![]()
|
![]()
|
Показательное
распределение:
![]()
|
![]()
|
![]()
|
Нормальное
распределение:
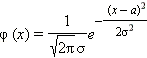
|
Mx = a |
Dx = σ2 |
Логарифмически-нормальное
распределение:
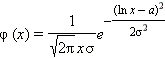
|
![]()
|
![]()
|
