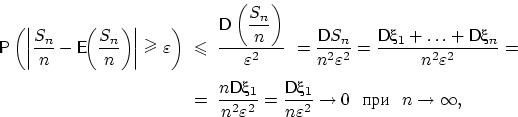30. Закон больших чисел.

Говорят, что последовательность случайных величин с конечными первыми моментами удовлетворяет закону больших чисел (ЗБЧ), если

(1)

Законами больших чисел принято называть утверждения о том, при каких условиях последовательность случайных величин удовлетворяет закону больших чисел, т.е. обладает свойством (1).

Выясним сначала, когда выполнен ЗБЧ для последовательности независимых и одинаково распределённых случайных величин.

Теорема (ЗБЧ Чебышёва). Для любой последовательности попарно независимых и одинаково распределённых случайных величин с конечным вторым моментом имеет место сходимость:

(2)

ЗБЧ утверждает, что среднее арифметическое большого числа случайных слагаемых «стабилизируется» с ростом этого числа. Как бы сильно каждая случайная величина не отклонялась от своего среднего значения, при суммировании эти отклонения «взаимно гасятся», так что среднее арифметическое приближается к постоянной величине.

В дальнейшем мы увидим, что требование конечности второго момента (или дисперсии) связано исключительно со способом доказательства, и что утверждение останется верным, если требовать существования только первого момента.

Доказательство.

Обозначим через сумму первых случайных величин. Из линейности математического ожидания получим:

Пусть . Воспользуемся неравенством Чебышёва:

(3)

так как . Заметим, что дисперсия суммы превратилась в сумму дисперсий в силу попарной независимости слагаемых, из-за которой все ковариации в свойстве 14 обратились в нуль при . Сумма же дисперсий слагаемых равняется из-за их одинаковой распределённости.

Замечание. Мы не только доказали сходимость, но и получили оценку для вероятности среднему арифметическому любого числа попарно независимых и одинаково распределённых величин отличаться от более, чем на заданное  :

(4)

Легко видеть, что попарную независимость слагаемых в ЗБЧ Чебышёва можно заменить их попарной некоррелированностью, ничего не меняя в доказательстве. ЗБЧ может выполняться и для последовательности зависимых и разнораспределённых слагаемых. Предлагаю читателям, проследив за равенствами и неравенствами (3), получить доказательство следующего утверждения, предлагающего достаточные условия выполнения ЗБЧ для последовательности произвольных случайных величин.

Теорема (ЗБЧ Маркова). Последовательность случайных величин с конечными вторыми моментами удовлетворяет ЗБЧ при выполнении любого из следующих условий:

1. если , т.е. если 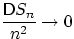при ;

2. если независимы и 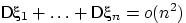  (т.е. если    )

3. если независимы, одинаково распределены и имеют конечную дисперсию (ЗБЧ Чебышёва).

Теорема Маркова утверждает, что ЗБЧ выполнен, если дисперсия суммы слагаемых растёт не слишком быстро с ростом .

Сильная зависимость слагаемых приводит обычно к невыполнению ЗБЧ. Если, например, и , то , и свойство (2) не выполнено (убедиться!). В этом случае ; для одинаково распределённых слагаемых дисперсия суммы быстрее расти не может.

Следующее утверждение мы докажем чуть позже. Сравните его условия с условиями ЗБЧ Чебышёва.

Теорема (ЗБЧ Хинчина). Для любой последовательности независимых (в совокупности) и одинаково распределённых случайных величин с конечным первым моментом имеет место сходимость:

Более того, в условиях теоремы имеет место и сходимость п. н. последовательности к . Это утверждение называется усиленным законом больших чисел (УЗБЧ) Колмогорова, и его мы доказывать не будем.

Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Я. Бернулли. В отличие от ЗБЧ Чебышёва, описывающего предельное поведение среднего арифметического случайных величин с произвольными распределениями, ЗБЧ Бернулли имеет дело лишь со схемой Бернулли.

Теорема (ЗБЧ Бернулли). Пусть событие может произойти в любом из независимых испытаний с одной и той же вероятностью , и пусть — число осуществлений события в испытаниях. Тогда . При этом для любого

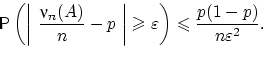
Доказательство. Заметим, что есть сумма независимых, одинаково распределённых случайных величин, имеющих распределение Бернулли с параметром (индикаторов того, что в соответствующем испытании произошло ): , где

и , . Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством (4).