28)Экономическая интерпретация числа е

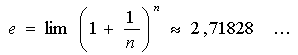
Способы определения

Число e может быть определено несколькими способами.

Через предел:

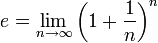(второй замечательный предел) .

Как сумма ряда:

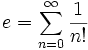или .

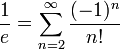Как единственное число a, для кот. выполняется

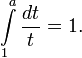
Как единственное положительное число a, для кот. верно

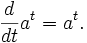
Свойства

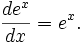Данное свойство играет важную роль в решении дифференциальных уравнений.Единственным решением дифференциального уравнения 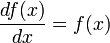явл. функ. , где c - произвольная константа.

29)Функции и отображения их области опред. И знач.

1.Функ. — это правило, согласно кот. каждому элементу из множества ставится в соответствие единственный элемент из множества . При этом говорят, что функ. задана на множестве , или что отображает в .

Если элементу сопоставлен элемент , то говорят, что элемент находится в функциональной зависимости от элемента . При этом переменная наз. аргументом функции или независимой переменной, множество наз. областью задания или областью определения функции, а элемент , соответствующий конкретному элементу — частным значением функ. в точке . Множество всех возможных частных значений функ. наз. её областью значений или областью изменения.

Если задана функция , кот. определена на множестве и принимает значения в множестве , то есть, функция отображает множество в , то

область определения функ. (множество ) обозначается

область значений функ. (множество ) обозначается ( )

основные элементарные функ.

1.постоянная ;

2.степенная , задано;

3показательная ;

4.логарифмическая ;

5.тригонометрические  ;

6.обратные тригонометрические ;

свойства основных элементарных функ. по схеме:

1.область определения функ.;

2.поведение функ. на границах области определения, вертикальные асимптоты.4.проверка на четность и нечетность;5.область значений функции;6.промежутки возрастания и убывания, точки экстремума;

7.промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба 8.наклонные и горизонтальные асимптоты;9.особые точки функ;10.особые свойства некоторых функ. (напр, наименьший положительный период у тригонометрических функций).

Понятие сложной функ.

Пусть функ. z = f(x,y) определена в некот. окрестности точки (x₀, y₀) . Пусть ее аргументы x и y в свою очередь явл. функциями x = x(t) , y = y(t) и определены в некоторой окрестности точки t₀ , причем x(t₀) = x₀ , y(t₀) = y₀ .

Тогда в окрестности точки t₀ определена сложная функ. аргумента t Z = f(x(t), y(t)).

Аналогично определяется сложные функции любого числа переменных.

Напр., если x и y — функции 2–х переменных: x = x(u,v) и y = y(u,v) , то функция z = f(x,y) явл. сложной функцией двух переменных u и v : Z = f(x(u,v), y(u,v)).

Функция одной переменной. Определение предела функ. в точке по Коши. Число b наз. пределом функ. у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа  сущ. такое положительное число , что при всех х ≠ а, таких, что |x – a | < , выполняется неравенство | f(x) – a | <  .

Указанный предел обозначается так:

Геометрически сущю предела функ. в точке по Коши означает, что для любого числа  > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2 > 0, высотой 2 и центром в точке (а; b), что все точки графика данной функ. на интервале (а–; а + ), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике – см. рис.:

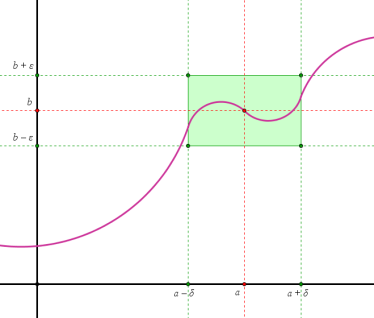
30) Функ. одной переменной. Определение предела функ. в точке по Коши.Число b наз. пределом функ. у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e сущ. такое положительное число d,что при всех х≠а, таких, что |x – a | < d, выполняется неравенство | f(x) – a | < e .

Определение предела функции в точке по Гейне. Число b наз. пределом функ. у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {x_n}, сходящейся к а (стремящейся к а, имеющей пределом число а), причем ни при каком значении n х_n ≠ а, последовательность {y_n = f(x_n)} сходится к b.

Данные определения предполагают, что функция у = f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а.

Определения предела функ. в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму.

Указанный предел обозначается так:

Геометрически существование предела функ. в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функ. на интервале (а– d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике – см. рис.:

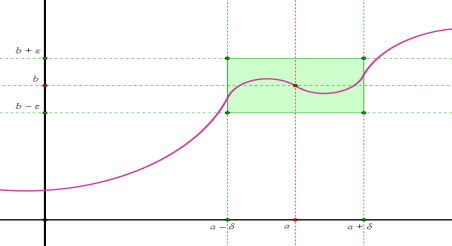
ТЕОРЕМА 1. Предел суммы двух функ.при x стремящемся к a равен сумме пределов этих функ.

ТЕОРЕМА 2. Предел произведения двух функ. при x стремящемся к a равен произведению пределов этих функ.

ТЕОРЕМА 3. Предел частного двух функ. при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля Теоремы:

1)Предел суммы двух функ. равен сумме их пределов: .

Доказательство:

Пусть  , . Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать:  и  . Следовательно,  , где  - бесконечно малая функция .Тогда по теореме о связи функ., её предела и бесконечно малой функ. можно записать  , или  .

2)Предел произведения двух функций равен произведению их пределов: .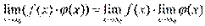

Доказательство:

Пусть  , . Тогда  и  . Следовательно

,

.

Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда  , т.е.  .

2)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен: .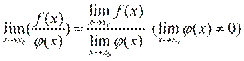

Доказательство:

Пусть  , . Тогда  и  . Тогда  . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.

Поэтому  , т.е.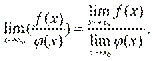 

о пределе сложной функции

Если сущ.конечный предел

а функция f(u) непрерывна в точке  , то

Для непрерывных функ. символы предела и функ. можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функ.

31) Предел ф-ции 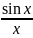d точке x=0,сущ.и равен 1

=1 - это первый замеч. предел.

Предел ф-ции f(x) = (1+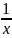 )в степени x… при x →∞ сущ. и равен e…

(1+ )в степени x=е --это второй замеч. предел