57)Интегрирование тригонометрических функций

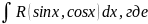
Интегралы вида 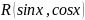-рациональная функ.от 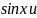cosx, приводятся к интегралам от рац.функций с помощью универсальной тригон.подстановки tg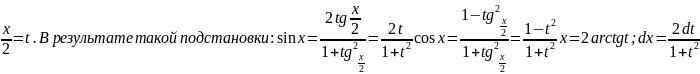

1)Если R(sinx,cosx)-нечётная функ.относительно sinx,т.е.если R(-sinx,cosx)=- R(sinx,cosx),то интеграл рационализируется подстановкой cosx=t 2) Если R(sinx,cosx)-нечётная функ.относительно cosx,т.е.если R(sinx,-cosx)=- R(sinx,cosx),то интеграл рационализируется подстановкой sinx=t 3) Если R(sinx,cosx)-чётная функ.относительно sinx и cosx,т.е.если R(-sinx,-cosx)= R(sinx,cosx),то применяется подстановка tgx=t

При вычислении интегралов 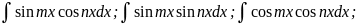используются формулы 1) 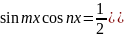2)

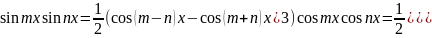
58)Определенный интеграл.

Если сущ.конечный предел интегральной суммы при n→∞, Δх →0 независимо от способа разбиения, независимо от выбора точек 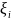, то этот предел наз. определённым интегралом данной функ.,а функ. - интегрируемой

Условие интегрируемости функ.

Если этот предел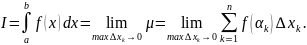

Сущ. ,то ф-ция наз. интегрируемой на [a;b].

59.)Основные свойства определённого интеграла

1. 

2. 

3. ,

4. 

5. 

6. 

7. 

8. 

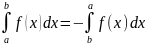
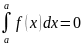
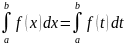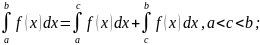
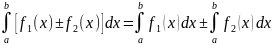
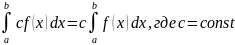
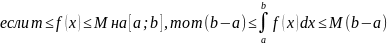
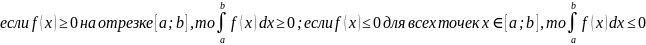
9. Если

10. 

11. 

12. 

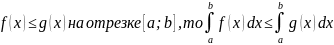
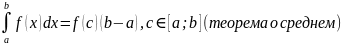
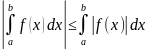
60.) Если функ. F(x) – какая- либо первообразная от непрерывной функ. f(x), то 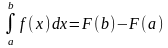это выражение известно под назв. формулы Ньютона – Лейбница.Доказ.: Пусть F(x)–первообразная функ.ю.Б f(x).Тогда в соответствии с приведенной выше теоремой, функция 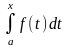- первообразная функция от f(x).Но т.к.функ.может иметь бесконечно много первообразных, кот. будут отличаться друг от друга только на какое – то постоянное число С, то 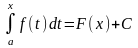при соответствующем выборе С это равенство справедливо для любого х, т.е. 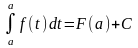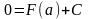при х 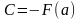= а: Тогда 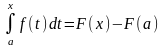.А при х = b: 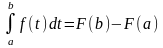Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

61.)Применение определённого интеграла для вычисления площадей фигур, длин дуг плоских кривых и объёмов тел.

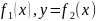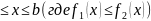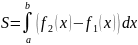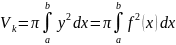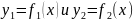
Площадь криволинейной трапеции. Пусть плоская фигура предст. собой криволинейную трапецию, ограниченную непрерывными кривыми y= , a и двумя отрезками прямых x=a, x=b.Тогда площадь фигуры вычисляется по формуле .Если криволинейная трапеция, ограниченная кривой y=f(x) и прямыми y=0, x=a, x=b, вращается вокруг оси Ох, то объём тела вращения вычис. по форм. .Если фигура, ограниченная кривыми 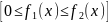и прямыми x=a, x=b, вращается вокруг оси Ох, то объём тела вращения находится по форм.

62.)Несобственные интегралы

Несобственными интегралами наз. интегралы с бесконечными пределами и интегралы от неограниченных функций. Пусть функция f(x) непрерывна на промежутке 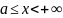, тогда она непрерывна на любом отрезке [a;b], 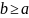, а следовательно, сущ. интеграл. Несобственный интеграл от функции f(x) в пределах от 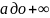определяется равенством

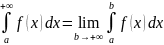
Если этот предел сущ. и конечен, то несобственный интеграл наз. сходящимся; если же предел не сущ. или равен бесконечности – расходящимся.

63) .Обыкновенным дифференциальным ур-ем(ОДУ) называют ур-ие,связывающее независимую переем X меняющуюся на некот интервале x О неизвестную ф-ию y(x) и её производную , .

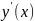В общем виде ОДУ можно записать так: F(x,y,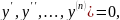 где F-известная ф-ия от (n+1)-переменных.

Порядком ДУ назыв max порядок производной неизв ф-ии входящей в ур-е.

Решением ДУ назыв ф-ия y=φ(x) такая,что при подстановке в данное ур-е получается верное тождество.

Т.о. ОДУ имеет бесконечно много решений.

График решения ДУ назыв интегральной кривой.

Решение ДУ содержащего const С назыв общим решением ДУ. Чтобы выделить единств решение необходимо наложить дополнит усл-е y(x₀)=y₀, кот назыв условием Коши.

Задача Коши(задача с начальным усл-ем). Пусть ф-ия а(чбн) определена в некот области D. (x₀,y₀)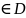 . Требуется найти реш-е ур-я F(x,y,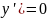 , удовлетворяющее усл-ю y(x₀)=y₀

64) Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p(x) и h(y) − непрерывные функции.  Рассматривая производную y' как отношение дифференциалов  , перенесем dx в правую часть и разделим уравнение на h(y):

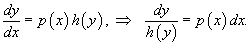
Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.  Обозначив 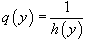 , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования.  Вычисляя интегралы, получаем выражение

описывающее общее решение уравнения с разделяющимися переменными.

определение однородного дифференциального уравнения

Дифференциальное уравнение первого порядка

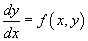
Наз. однородным, если правая часть удовлетворяет соотношению

для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:

Однородное дифференциальное уравнение можно также записать в виде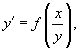

или через дифференциалы:

где P(x,y) и Q(x,y) − однородные функ. одинакового порядка.

65)Линейные ДУ I порядка. называется уравнение вида у΄+р(х)у=f(x),где р(х) и (х)-заданные непрерывные функции.Решение линейного уравнеия сводиться к решению дифференциальных уравнений с разделяющимеся переменными относительно каждой из вспомогательной функции.