23)Решение системы линейных уравнений матричным методом

Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда слу можно записать в матричной форме AX=B. Умножив это матричное уравнение на A^-1, получим A^-1AX= A^-1B, откуда EX=X=A^-1B. Следовательно, матрица-решение X легко находится как произведение A^-1 и B.

2 тип уравнения: Х*А=В,следовательно Х=В*А^-1 ;3 тип уравнения: А*Х*В=С,следоват. Х= A^-1 * С*В^-1

24) Метод Гаусса.

Решение систем линейных уравнений методом Гаусса

Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.

Пусть дана система уравнений

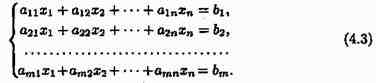
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид где

Коэффициенты aii называются главными элементами системы.

На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

25) Теорема Кронекера – Капелли

Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. R(A) = r(A\ B).

Док-во.1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А^* не изменяют ранга.

2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, т.е верна запись, приведенная выше.

Рангом матрицы А называется наибольший из порядков её миноров не равных нулю.

Базисным минором называется любой из миноров матрицы А, порядок которого равен r(A).

Теорема 1. При элементарных преобразованиях ранг матрицы не изменяется.

Теорема 2. Ранг ступеньчатой матрицы равен количеству её не нулевых строк.

26) Комплексным числом Z называют упорядоченную пару Z= (xy) действительных чисел .

Формы представления комплексных чисел

Тригонометрическая форма комплексного числа. Формула Муавра

 слева у нас алгебраическая форма числа, справа тригонометрическая форма числа.

r - модуль комплексного числа z.

 - главный аргумент комплексного числа z.

Алгебраическая форма комплексного числа

 Комплексным числом называется пара действительных чисел (x,y). Причем комплексное число z = x + i*y, где i - мнимая единица. Данное определение и задает представление комплексного числа в алгебраической форме. Введем ещё несколько определений, в частности поясним понятие аргумента и модуля комплексного числа. 

Действия над комплексными числами

• Сравнение

 означает, что   и   (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

• Вычитание

• Умножение

• Деление

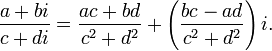
Формула Эйлера утверждает, что для любого вещественного числа  выполнено следующее равенство:

,

где   — основание натурального логарифма,

i— мнимая единица.

При помощи формулы Эйлера можно определить функции   и   следующим образом:

,

.

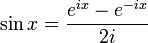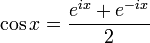27) Числовые последовательности предст. собой бесконечные упорядоченные множества чисел.

Саму последовательность обозначают , общий член последовательности обозначают . Числа наз. членами последовательности: — первый член последовательности, — второй член последовательности, — -ый член последовательности и т.д.

Бесконечно малой последовательностью наз. такая последовательность, что для сколь угодно малой окрестности нуля, вне окрестности будет только счетное число элементов последовательности, а в самой окрестности бесконечное число элементов последовательности.

Последовательность наз. бесконечно малой, если . Напр., последовательность чисел  — бесконечно малая.

Функ. наз. бесконечно малой в окрестности точки , если .

Функ. наз. бесконечно малой на бесконечности, если либо .

Также бесконечно малой явл. функ., предст. собой разность функ. и её предела, то есть если , то , .

Бесконечно большой последовательностью наз. такая последовательность, что для сколь угодно малой окрестности нуля, вне окрестности будет бесконечное число элементов последовательности , а в самой окрестности только счетное число элементов последовательности.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака . То есть, напр., функ. , неограниченная с обеих сторон, не явл. бесконечно большой при .

Последовательность наз. бесконечно большой, если .

Функ. наз. бесконечно большой в окрестности точки , если .

Функ. наз. бесконечно большой на бесконечности, если либо .

Постоянное число а наз. пределом последовательности {x_n}, если для любого сколь угодно малого положительного числа ε > 0 сущ. номер N, что все значения x_n, у кот. n>N, удовлетворяют неравенству

                                                                               |x_n - a| < ε.   Монотонная последовательность — последовательность , удовлетворяющая одному из след. условий:

1. для люб. номера 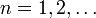выполняется неравенство 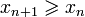(неубывающая последовательность),

2. для люб. номера выполняется неравенство 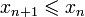(невозрастающая последовательность).

Среди монотонных последовательностей выделяются строго монотонные последовательности, удовлетворяющие одному из след. условий:

1. для люб. номера выполняется неравенство x_{n + 1} > x_n (возрастающая последовательность);

2. для люб. номера выполняется неравенство x_{n + 1} < x_n (убывающая последовательность).