26. Дискретная двухточечная краевая задача. Априорная оценка решения разностной схемы (без доказательства).

Двухточечная краевая задача- это задача отыскания решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений на отрезке , в которой дополнительные условия накладываются в двух точках a и b- краях отрезка.

Смысл построения разностной схемы заключается в дискретизации краевой задачи, т.е. замене области непрерывного изменения аргумента сеткой- конечным набором точек.

-в результате дифференциальное уравнение оказалось его дискретным аналогом – разностным уравнением.

Обозначим : ,запишем систему сеточных ур-ий в следующем виде:

(1)

(2)-эту дискретную задачу принято называть разностной схемой.

Теорема

Для решения разностной схемы :

справедлива оценка:

Лемма

Для решения разностной схемы :

справедлива оценка:

Теорема

Для решения разностной схемы (1),(2) справедлива априорная оценка :

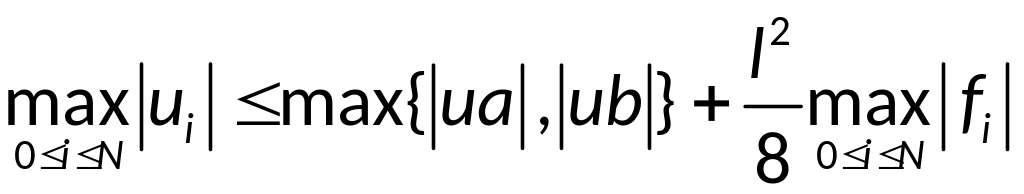
27. Дискретная двухточечная краевая задача. Устойчивость разностной схемы.

Двухточечная краевая задача- это задача отыскания решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений на отрезке , в которой дополнительные условия накладываются в двух точках a и b- краях отрезка.

Смысл построения разностной схемы заключается в дискретизации краевой задачи, т.е. замене области непрерывного изменения аргумента сеткой- конечным набором точек.

-в результате дифференциальное уравнение оказалось его дискретным аналогом – разностным уравнением.

Обозначим : ,запишем систему сеточных ур-ий в следующем виде:

(1)

(2)-эту дискретную задачу принято называть разностной схемой.

Устойчивость: Пусть - решение разностной схемы (1),(2), а - решение разностной схемы:

, где

Назовем разностную схему устойчивой, если при любых , , справедлива оценка:

(3)

Теорема

Для разностной схемы (1),(2) справедлива оценка (3) с постоянной К= .

28. Дискретная двухточечная краевая задача. Аппроксимация и сходимость разностной схемы.

Двухточечная краевая задача- это задача отыскания решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений на отрезке , в которой дополнительные условия накладываются в двух точках a и b- краях отрезка.

Смысл построения разностной схемы заключается в дискретизации краевой задачи, т.е. замене области непрерывного изменения аргумента сеткой- конечным набором точек.

-в результате дифференциальное уравнение оказалось его дискретным аналогом – разностным уравнением.

Обозначим : ,запишем систему сеточных ур-ий в следующем виде:

(1)

(2)-эту дискретную задачу принято называть разностной схемой.

Аппроксимация : Пусть -решение дифференциального уравнения . Назовем сеточную функцию -погрешностью аппроксимации разностного уравнения (1),справедливо равенство , означающее, что функция удовлетворяет разностному уравнению(1) с точностью до погрешности аппроксимации. Говорят, что разностное уравнение (1) аппроксимирует дифференциальное уравнение , если при , и аппроксимирует его с m-м порядком, если справедлива оценка

Лемма

Пусть коэф. q и f дважды непрерывно дифференцируемы на отрезке . Тогда разностное уравнение аппроксимирует дифференциальное уравнение со вторым порядком, причем справедлива оценка 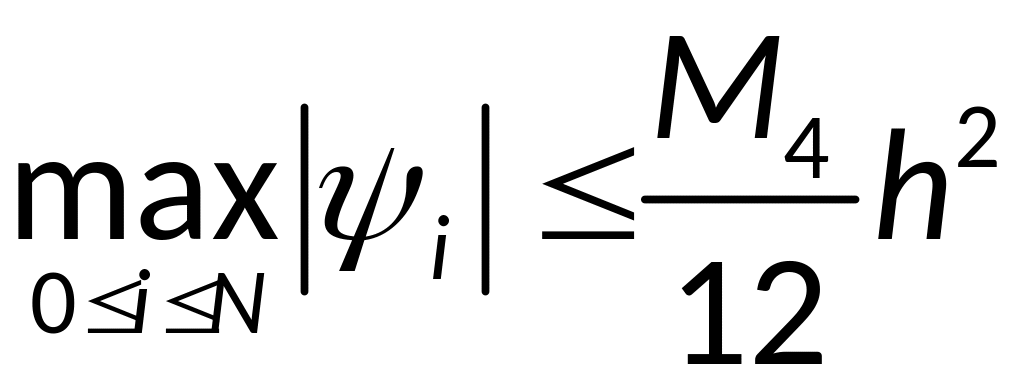(2),

Док-во : В силу определения погрешности аппроксимации имеем 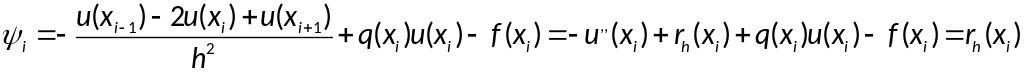,где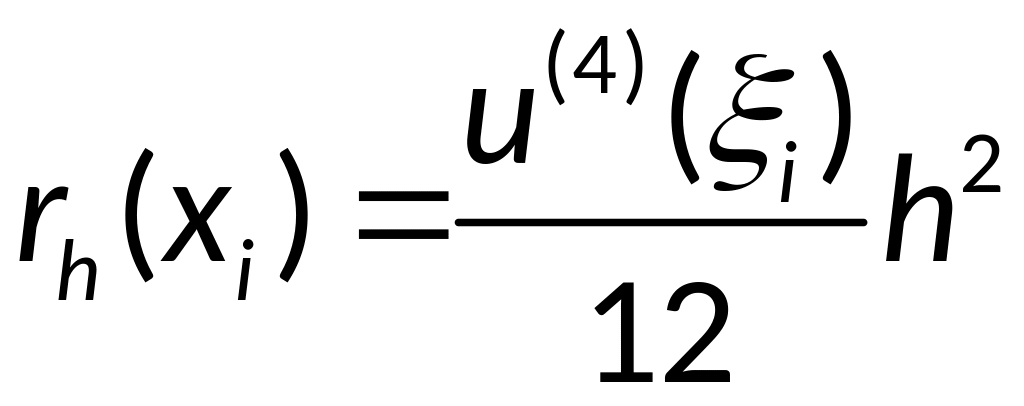 -погрешность аппроксимации производной ее разностным аналогом.

Сходимость : Пусть -решение краевой задачи, а -решение соответствующей разностной схемы. Назовем погрешностью разностной схемы сеточную функцию , принимающую значения в узлах сетки. Будем говорить, что разностная схема сходится при , если при , и сходится с m-м порядком точности, если для погрешности справедлива оценка .

Теорема

Пусть коэф. q и f дважды непрерывно дифференцируемы на отрезке . Тогда для погрешности разностной схемы справедлива оценка , где .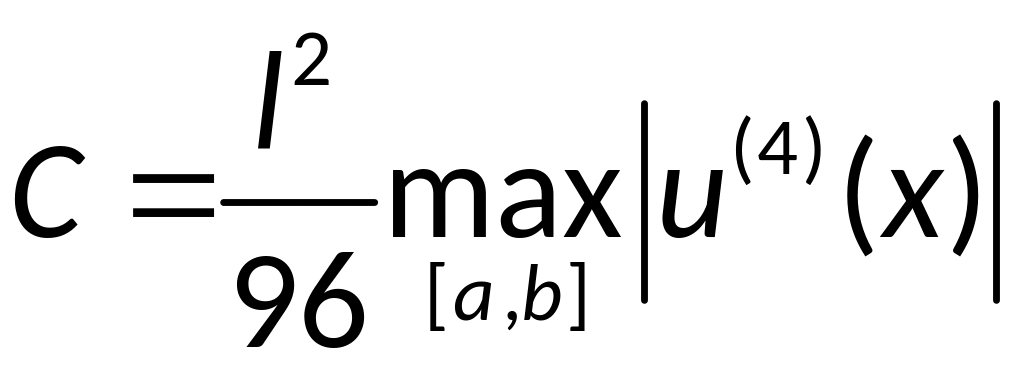

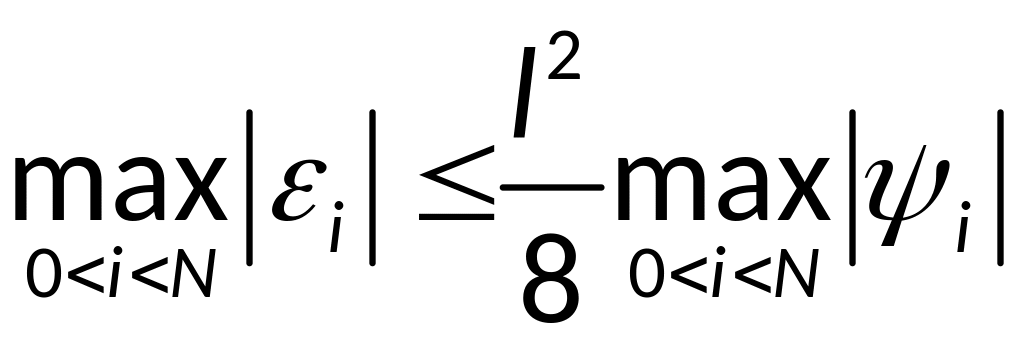Док-во : Введем сеточную ф-ию ,значения которой в узлах сетки совпадают с точными значениями решения краевой задачи, т.е. .Равенство означает, что можно рассматривать как решение разностной схемы . Справедлива оценка (3). Учитывая теперь неравенство(2), из (3) получаем оценку.