
- •Численное интегрирование: вывод формулы прямоугольников и оценки погрешности.
- •Численное интегрирование: вывод формулы трапеций и оценки погрешности.
- •Численное интегрирование: формула Симпсона и оценка погрешности.
- •Правило Рунге оценки погрешностей. Уточнение по Рунге.
- •Численное дифференцирование. Вычисление первой и второй производной, оценки погрешности.
- •Задача Коши для дифференциального уравнения первого порядка: постановка задачи, её разрешимость, устойчивость на конечном отрезке.
- •Задача Коши для дифференциального уравнения первого порядка: устойчивость по правой части и на неограниченном промежутке.
- •Численные методы решения задачи Коши. Основные понятия и определения: дискретная задача Коши, явные и неявные методы, устойчивость, аппроксимация, сходимость.
- •Численные методы решения задачи Коши. Метод разложения в ряд Тейлора.
- •Численные методы решения задачи Коши. Метод Эйлера, его геометрическая интерпретация, оценка погрешности метода Эйлера.
- •13.Численные методы решения задачи Коши: модификации метода Эйлера второго порядка точности, геометрическая интерпретация, оценка погрешности методов.
- •14. Численные методы решения задачи Коши: методы Рунге–Кутты. Идея построения расчетных формул. Метод Рунге-Кутты 4-го порядка точности.
- •16. Явные одношаговые методы. Локальная и глобальная погрешности. Оценка погрешности по правилу Рунге.
- •17. Аппроксимация, устойчивость и сходимость явных методов решения задачи Коши.
- •15. Сходимость метода Эйлера.
- •18. Решение задачи Коши для систем дифференциальных уравнений.
- •19.Решение задачи Коши для уравнения m-го порядка.
- •20. Многошаговые методы. Вывод формул явного метода Адамса-Башфорта. Порядок аппроксимации метода.
- •21. Многошаговые методы. Вывод формул неявного метода Адамса-Моултона. Порядок аппроксимации метода.
- •22. Устойчивость численных методов. Понятие нуль-устойчивости.
- •23. Жесткие задачи: понятие о жестких задачах, жесткие системы дифференциальных уравнений. Методы их решения.
- •24. Постановка двухточечной краевой задачи. Основные теоремы (без доказательств) о разрешимости и устойчивости дифференциальной задачи.
- •25. Дискретная двухточечная краевая задача. Теорема о существовании решения разностной схемы.
- •26. Дискретная двухточечная краевая задача. Априорная оценка решения разностной схемы (без доказательства).
- •27. Дискретная двухточечная краевая задача. Устойчивость разностной схемы.
- •28. Дискретная двухточечная краевая задача. Аппроксимация и сходимость разностной схемы.
- •29. Решение сеточных уравнений методом прогонки. Правило Рунге оценки погрешности.
- •30. Применение метода конечных разностей при решении двухточечной краевой задачи в случае переменного коэффициента теплопроводности.
- •31. Метод баланса построения разностных схем для решения двухточечной краевой задачи.
- •32. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: построение явной схемы и оценка погрешности.
- •33. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: условная устойчивость явной схемы.
- •34. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: неявная схема, абсолютная устойчивость неявной схемы.
- •35.Метод переменных направлений решения двумерной начально-краевой задачи для уравнений теплопроводности.
- •40. Метод конечных разностей решения задачи Дирихле для уравнения Пуассона. Итерационные методы решения сеточных уравнений: метод Зейделя.
Численное дифференцирование. Вычисление первой и второй производной, оценки погрешности.
Применяется, когда функцию невозможно продифференцировать аналитически. Например, функция задана таблицей. Кроме того, формулы численного дифференцирования широко используются при разработке вычислительных методов решения различных задач.
Исходя из определения
первой производной:
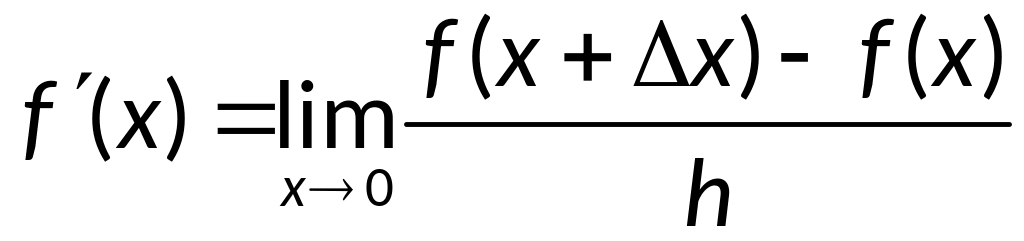
 - левая разностная
производная
- левая разностная
производная
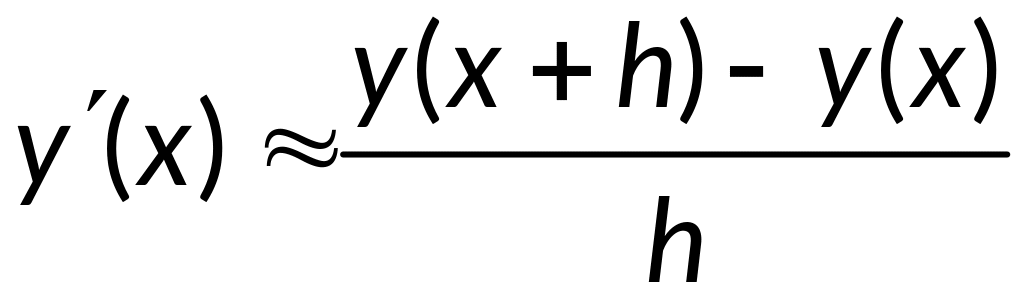 - правая разностная
производная
- правая разностная
производная
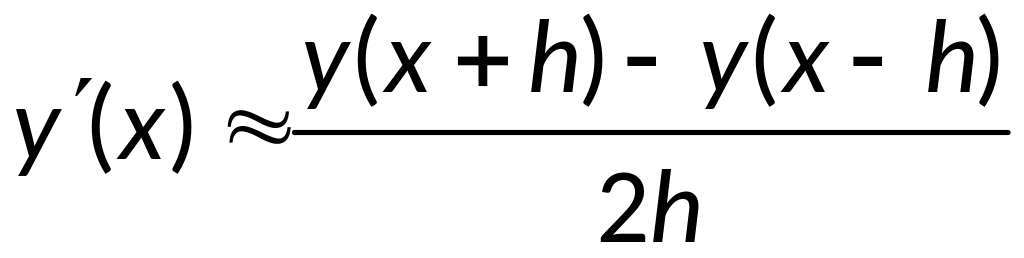 - центральная
разностная производная
- центральная
разностная производная
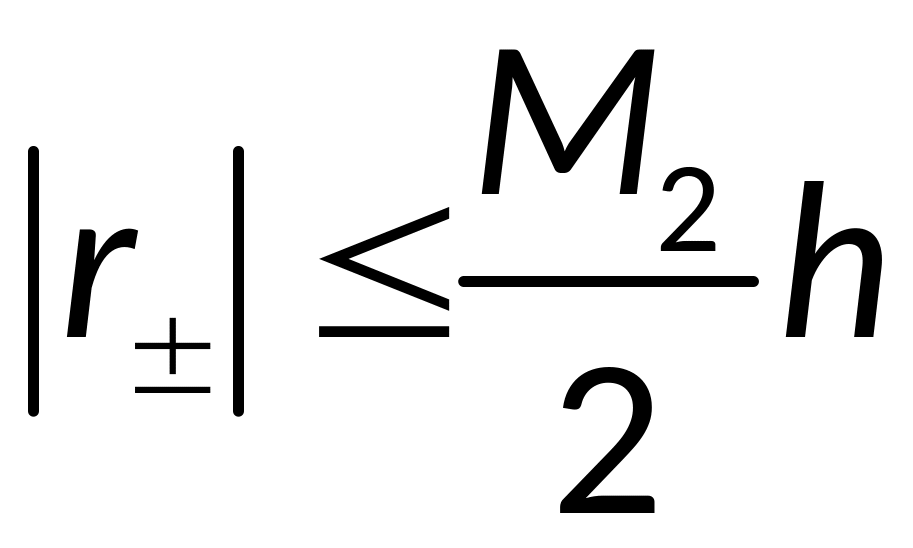 - погрешность
аппроксимации (1-й порядок точности)
- погрешность
аппроксимации (1-й порядок точности)
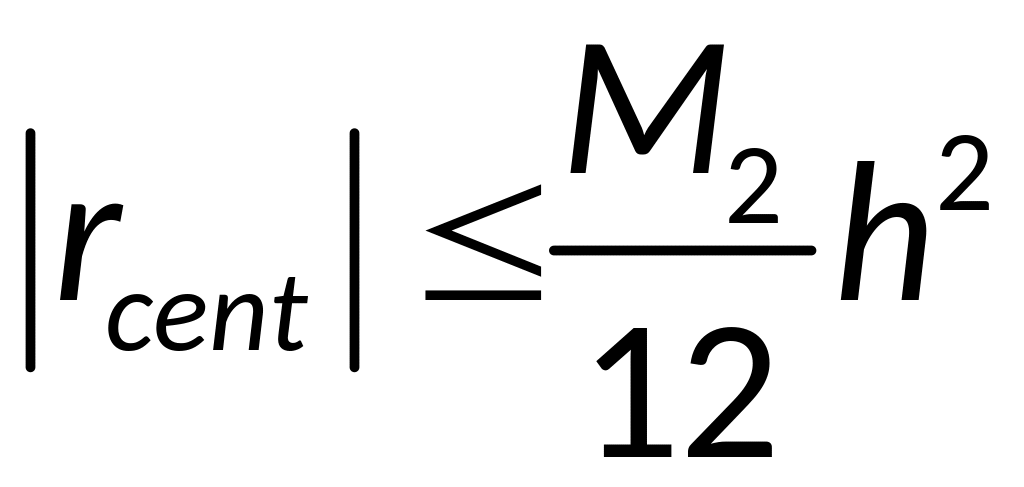 - погрешность
аппроксимации (2-й порядок точности)
- погрешность
аппроксимации (2-й порядок точности)
Вывод погрешности:
по формуле Тейлора:
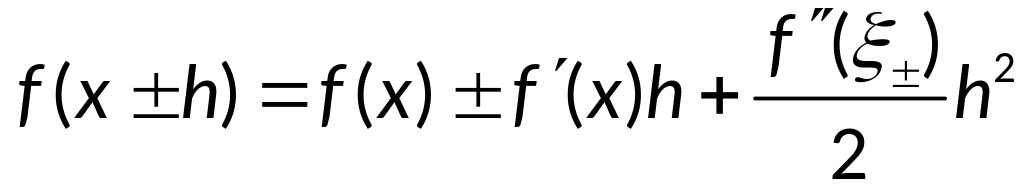
![]() - некоторые точки,
расположенные на интервалах (x,
x+h)
и (x-h,
x)
соответственно.
- некоторые точки,
расположенные на интервалах (x,
x+h)
и (x-h,
x)
соответственно.
Подставляя
разложения в
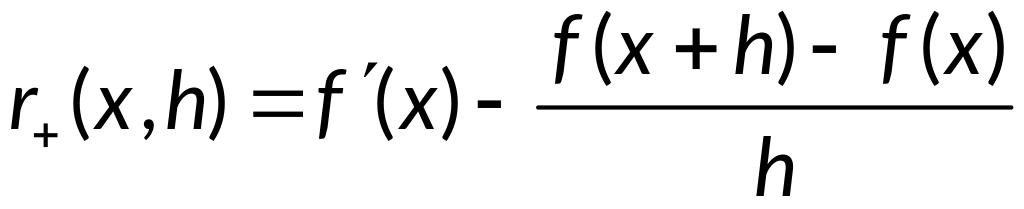 ,
,
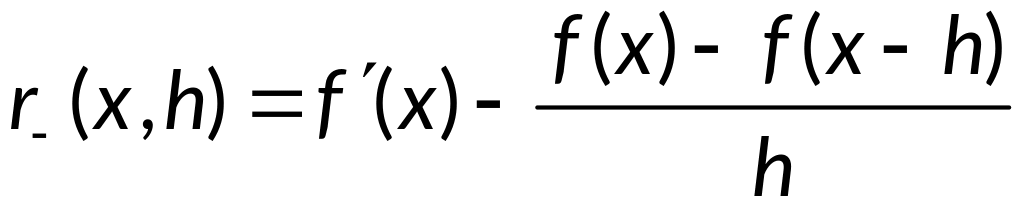
получаем:
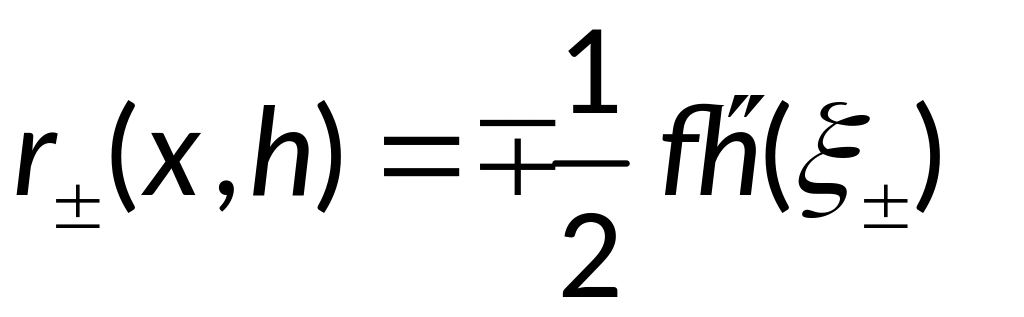 .
.
Для центральной разностной производной надо разложить в ряд до 3-й производной.
 ,
,
![]() - интерполирование
вперёд.
- интерполирование
вперёд.
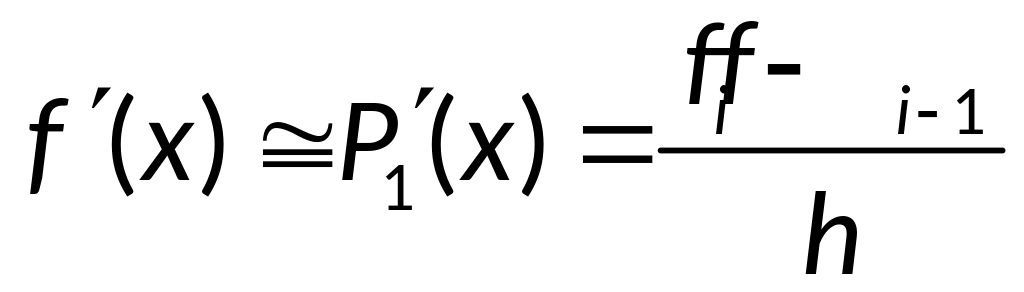
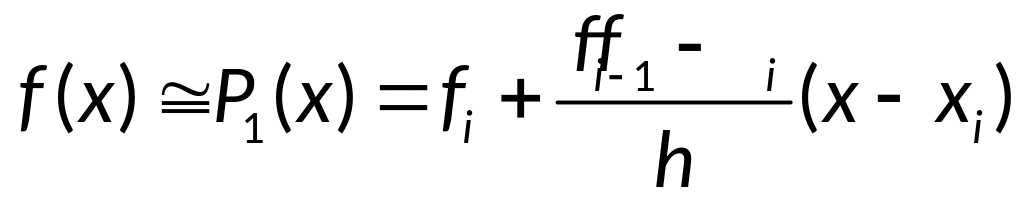 - интерполирование
назад.
- интерполирование
назад.
Используя 3 узла интерполяции, возьмём многочлен 2-й степени от x:
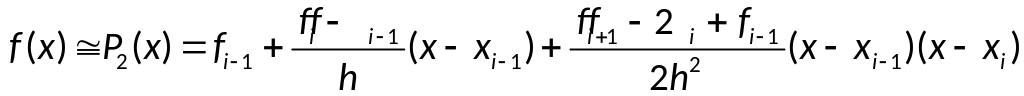
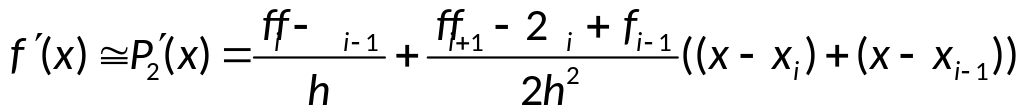
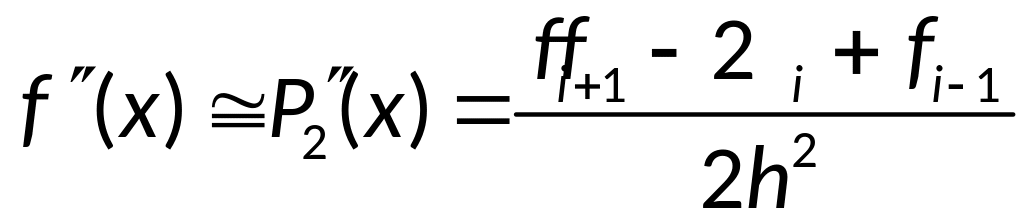
Подставляя в первую
производную
![]() ,
можно получить формулы второго порядка
точности для вычисления 1-й производной.
,
можно получить формулы второго порядка
точности для вычисления 1-й производной.
Задача Коши для дифференциального уравнения первого порядка: постановка задачи, её разрешимость, устойчивость на конечном отрезке.
Часто приходится иметь дело с процессами, характеристики которых непрерывным образом меняются со временем t. Соответствующие явления подчиняются физическим законам, которые формулируются в виде дифференциальных уравнений. Задача Коши (начальная задача) – описывает развитие процессов во времени. Начальные условия считаются известными.
Постановка задачи: требуется найти функцию y(t), при t>t0, дифф. ур-я первого порядка, графиком которой будет являться интегральная кривая.
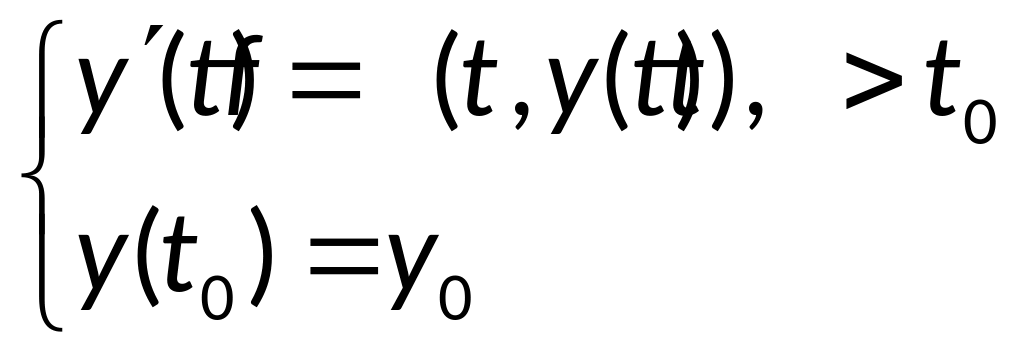
Разрешимость
задачи Коши: Пусть ПТ
– множество точек (t,y),
удовлетворяющих условию
![]() ,
,
![]() ;
это множество будем называть полосой.
;
это множество будем называть полосой.
Теорема:
Пусть функция f(t,y)
определена и непрерывна в полосе ПТ.
Предположим, что она удовлетворяет
условию Липшица
![]() для всех
и произвольных
для всех
и произвольных
![]() ,
где L
– некоторая постоянная (постоянная
Липшица).
,
где L
– некоторая постоянная (постоянная
Липшица).
Тогда для каждого начального значения y0 существует единственное решение y(t) задачи Коши, определённое на отрезке [t0,T].
Замечание: для
дифференцируемых по y
функций f
условие Липшица выполняется тогда и
только тогда, когда для всех
![]() справедливо равенство:
справедливо равенство:
![]() .
.
Теорема: Пусть функция f непрерывно дифференцируема m раз в полосе ПТ. Тогда если функция y является на отрезке [t0,T] решением задачи Коши, то она непрерывно дифференцируема m+1 раз на этом отрезке.
Устойчивость на
конечном отрезке: Пусть
![]() - возмущённое начальное значение,
- возмущённое начальное значение,
![]() - его погрешность, а
- его погрешность, а
![]() - решение задачи Коши:
- решение задачи Коши:
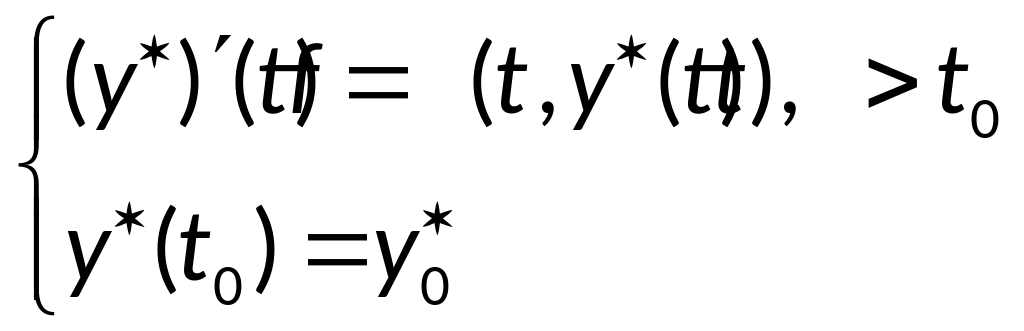
Вычтем из обычного
уравнения возмущённое, и воспользуемся
формулой конечных приращений Лагранжа:
![]() ,
,
![]() ,
где
,
где
![]() - некоторое промежуточное между
- некоторое промежуточное между
![]() и
значение.
и
значение.
Получим, что
погрешность
![]() удовлетворяет
удовлетворяет
![]() и
и
![]() .
.
Решение выражается
формулой:
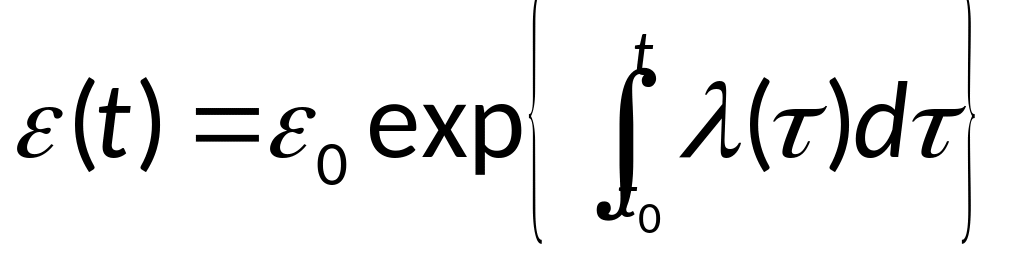 .
.
Т.о. величина
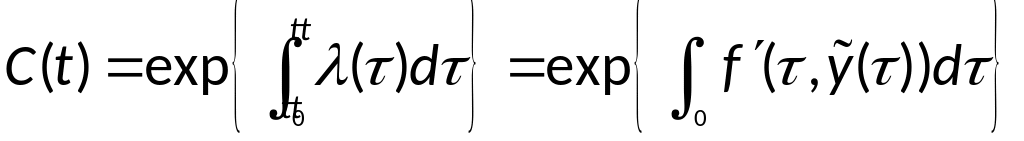 играет в задаче Коши роль коэффициента
роста погрешности.
играет в задаче Коши роль коэффициента
роста погрешности.
![]() - окажется
ограниченным, если задача решается на
конечном отрезке [t0,T].
- окажется
ограниченным, если задача решается на
конечном отрезке [t0,T].
![]()
![]() для всех
,
где
для всех
,
где
 при
при
![]() справедлива оценка:
справедлива оценка:
![]()
Выражающая устойчивость на конечном отрезке [t0,T].
