9. Задача Коши для дифференциального уравнения первого порядка: устойчивость по правой части и на неограниченном промежутке.

Часто приходится иметь дело с процессами, характеристики которых непрерывным образом меняются со временем t. Соответствующие явления подчиняются физическим законам, которые формулируются в виде дифференциальных уравнений. Задача Коши (начальная задача) – описывает развитие процессов во времени. Начальные условия считаются известными.

Постановка задачи: требуется найти функцию y(t), при t>t₀, дифф. ур-я первого порядка, графиком которой будет являться интегральная кривая.

Устойчивость по правой части: Будет ли решение задачи Коши устойчивым не только к погрешности начального значения, но и к погрешностям задания правой части уравнения?

Теорема: Пусть выполнены условия теоремы о разрешимости задачи Коши. И пусть y(t) – решение задачи, а - решение возмущённой задачи:

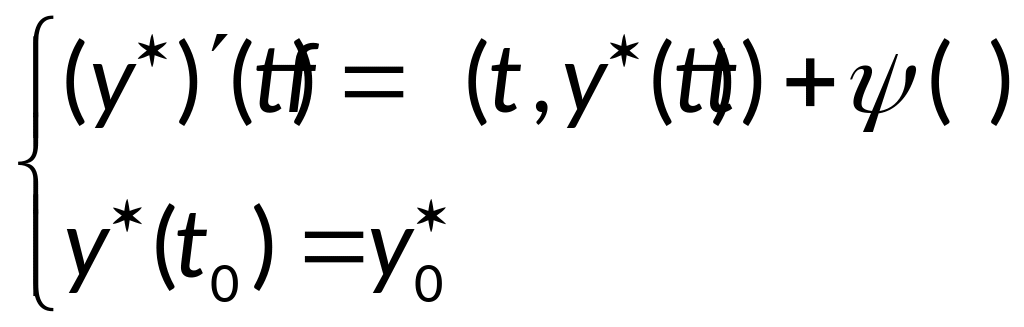
Тогда справедлива оценка: 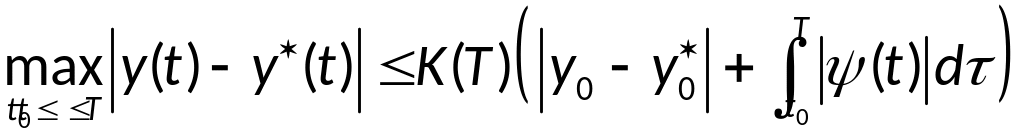, выражающая устойчивость на конечном отрезке [t₀,T] решения задачи Коши по начальным значениям и правой части. .

Устойчивость на неограниченном промежутке: Входящая в неравенство выше величина К(T) может неограниченно расти с ростом T, это означает, что допускается неограниченный при рост погрешностей. Т.е. при больших Т такая задача является плохо обусловленной.

Для того, что обусловленность задачи Коши не ухудшалась с ростом Т, достаточно потребовать, чтобы правая часть уравнения удовлетворяла неравенству для всех и произвольных y.

, где постоянная К не зависит от Т.

Если дополнительно известно, что при , то решение y(t) называют асимптотически устойчивым.

9. Численные методы решения задачи Коши. Основные понятия и определения: дискретная задача Коши, явные и неявные методы, устойчивость, аппроксимация, сходимость.

Первым этапом на пути построения численного метода решения задачи Коши состоит в замене отрезка [t₀,T] – области непрерывного изменения аргумента t – множеством , которое состоит из конечного числа точек t₀<t₁<…<t_N=T и называется сеткой. Сами точки t_n – называются узлами сетки, а величина h_n=t_n-t_n-1 – шагом сетки.

Сеточные функции – такие функции, которые определены лишь в узлах сетки.

Дискретная задача Коши: составление системы уравнений, решая которую можно последовательно находить значения сеточной функции , играющие роль приближений к значениям решения задачи Коши в узлах сетки .

- к-шаговый неявный метод (дискретное ур.).

- стартовые точки, которые необходимо задать.

Эту задачу будем называть дискретной задачей Коши.

При к=1 получаем: 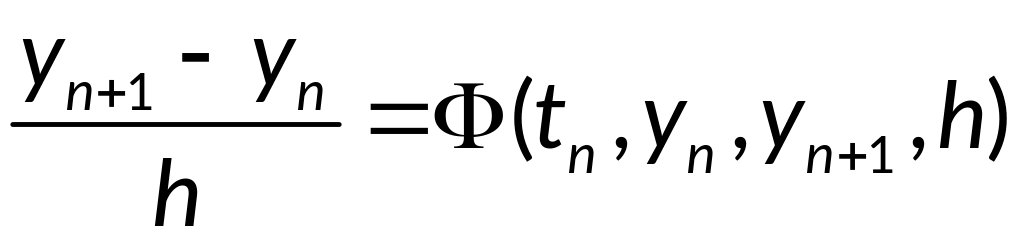- одношаговый метод.

Явные и неявные методы: методы, в которых функция не зависит от при вычислении значения называют явными. Методы, в которых функция зависит от , называют неявными.

Устойчивость: Опр. численный метод называют устойчивым, если выполняется следующее неравенство: , - возмущённая задача.

Опр. Будем называть многочлен - многочленом устойчивости численного метода, а уравнение - характеристическим уравнением метода.

Опр. Будем говорить, что выполнено корневое условие, если все корни многочлена устойчивости лежат внутри или на границе единичного круга комплексной плоскости и на границе круга нет кратных корней.

Опр. Метод называется абсолютно устойчивым при данном значении z, если все корни полинома устойчивости удовлетворяют корневому условию. Множество точек z комплексной плоскости, для которого метод является абсолютно устойчивым называют областью устойчивости метода. .

Опр. Численный метод называется А-устойчивым, если область абсолютной устойчивости включает в себя левую часть комплексной плоскости ReZ<0.

Аппроксимация + устойчивость = сходимость метода.

Опр. Пусть - собственные числа матрицы А, . Числом жёсткости называется величина 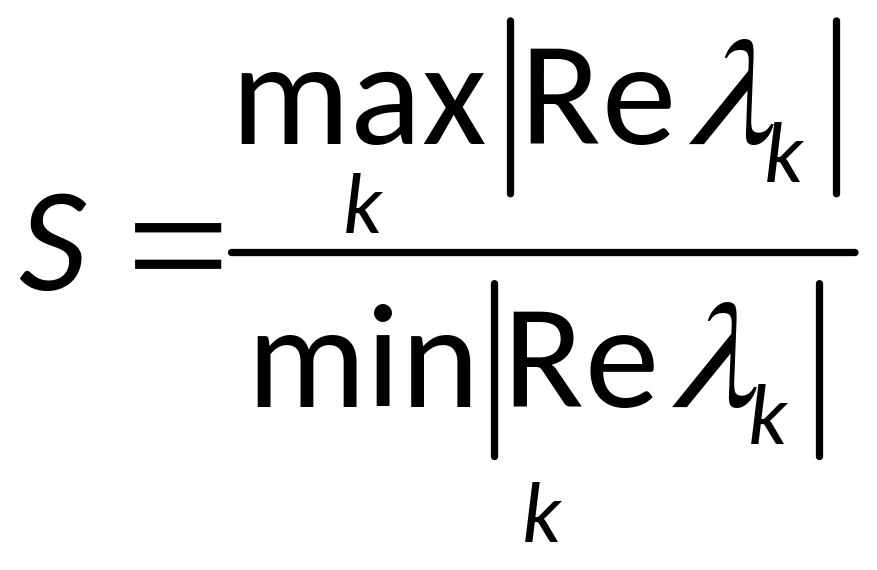, - жёсткая задача.

Разность называется локальной погрешностью метода (на шаге), то есть это погрешность, которую допускает за один шаг метод, стартовавший с точного решения.

Аппроксимация: Пусть y(t) – решение задачи Коши. Назовём сеточную функцию погрешностью аппроксимации. Говорят, что дискретное уравнение аппроксимирует дифференциальное уравнение, если при , и аппроксимирует его с р-ым порядком, если справедлива оценка: , .

Сходимость: Пусть y(t) – решение задачи Коши. Сеточную функцию в узлах - будем называть глобальной погрешностью. - мера абсолютной погрешности метода.

Численный метод решения задачи Коши называют сходящимся, если для него при . Принято говорить, что метод сходится с р-ым порядком точности, если для погрешности справедлива оценка: , .