32. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: построение явной схемы и оценка погрешности.

Постановка задачи:

найти U(x,t)

(1)

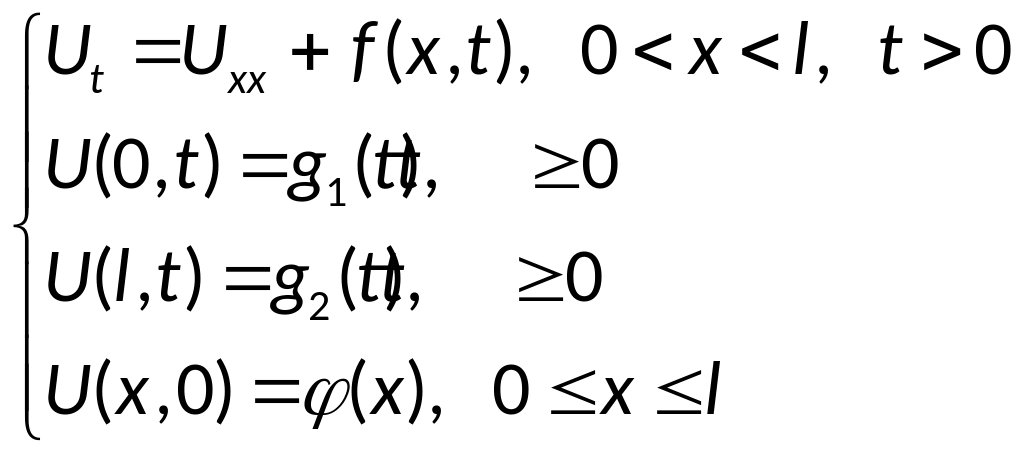
Функция U(x,t) имеет смысл температуры, а задача (1) описывает процесс теплопроводности в стержне длины l.

, - температура в концах стержня (ГУ 1-го рода)

- начальная температура

Дискретизация задачи (1):

; ;

; ;

- сетка узлов

Множество узлов , ,…, (2)

Называется j-ым слоем.

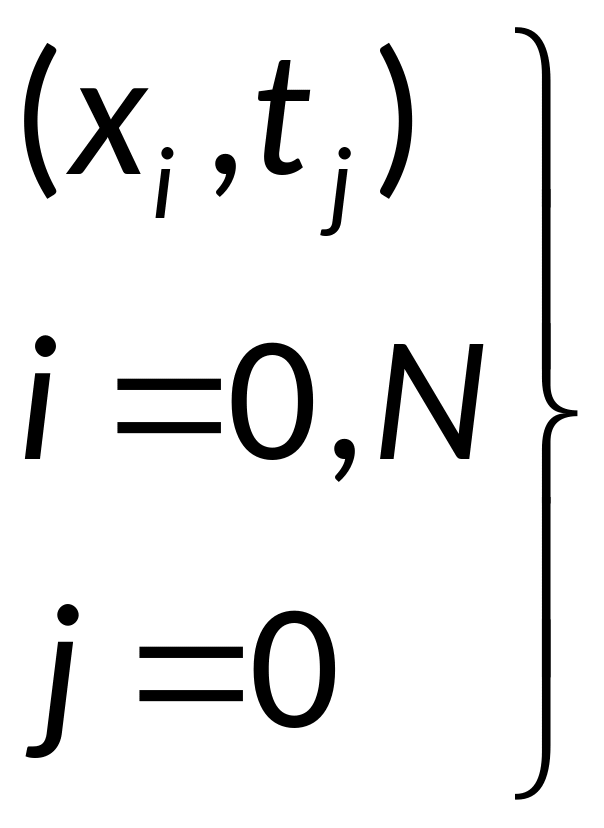- граничные узлы

- дискретное множество точек, представленное матрицей

Пострим разностную схему методом конечных разностей:

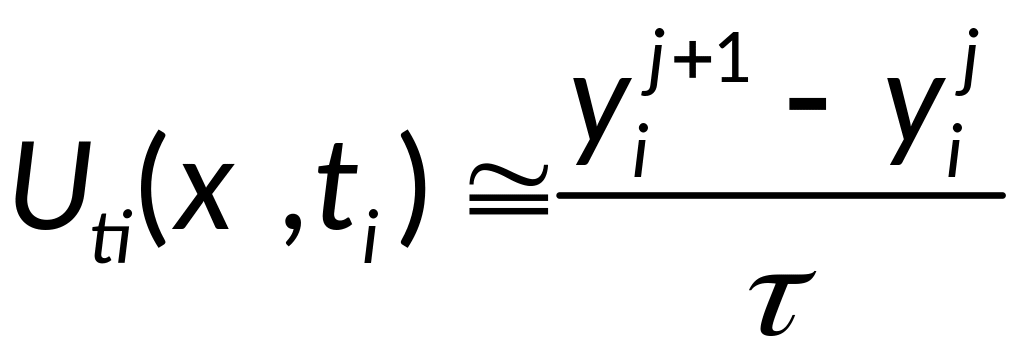- правая разностная аппроксимация

Явная разностная схема для уравнения теплопроводности:

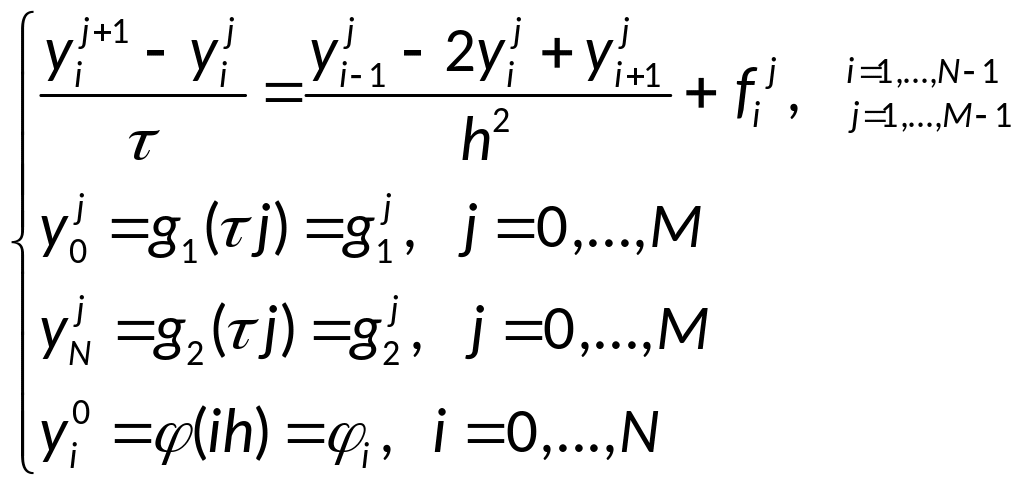
Разностная схема (2) называется явной, так как решение неизвестной находится по явной формуле, используя следующий четырёхточечный шаблон (смотри картинку).

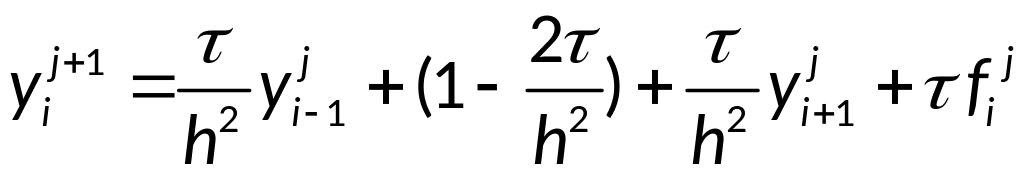; - коэффициент

33. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: условная устойчивость явной схемы.

Рассмотрим основное уравнение разностной схемы:

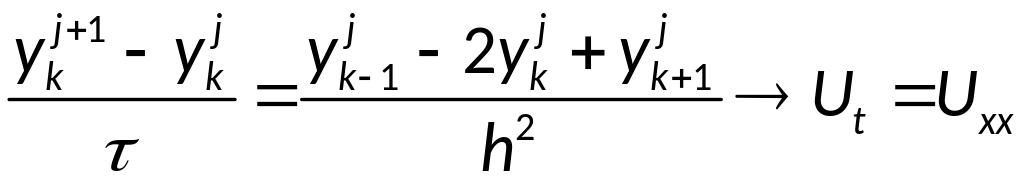
Предположим, что решение задачи можно представить в виде:

, где

i – мнимая единица

k – индекс точки

h – шаг

p – константа

q>1 – погрешность растёт неустойчивость

q 1 – погрешность не растёт устойчивость

Воспользуемся формулами: ; ; ;

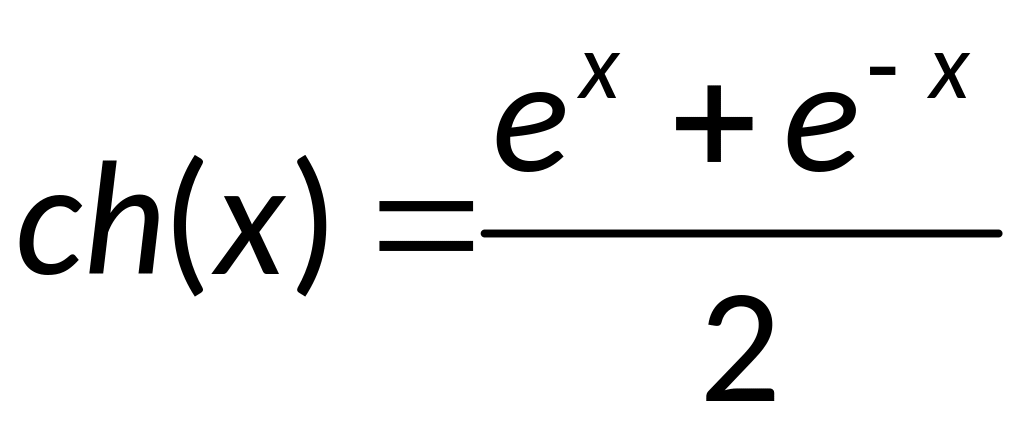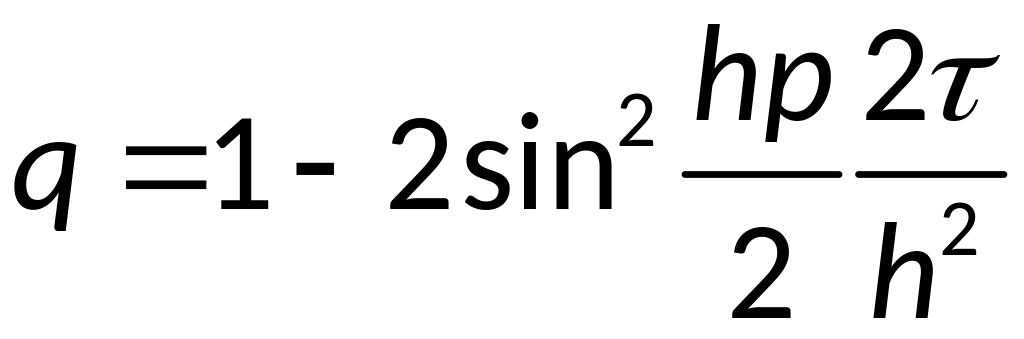
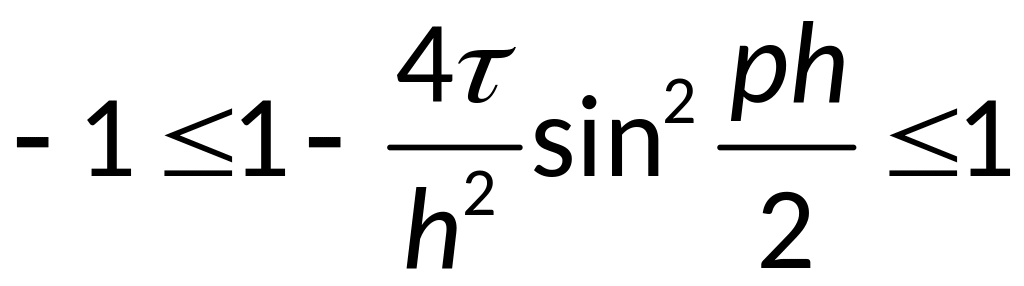
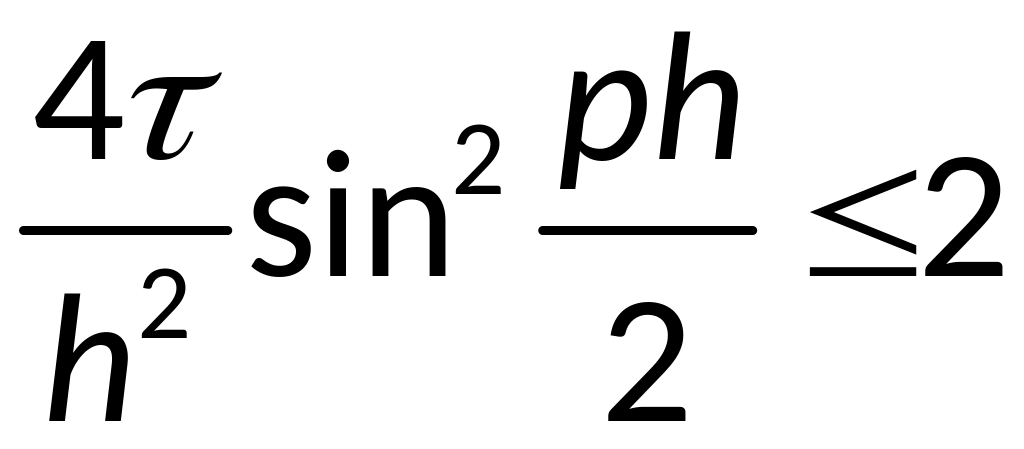
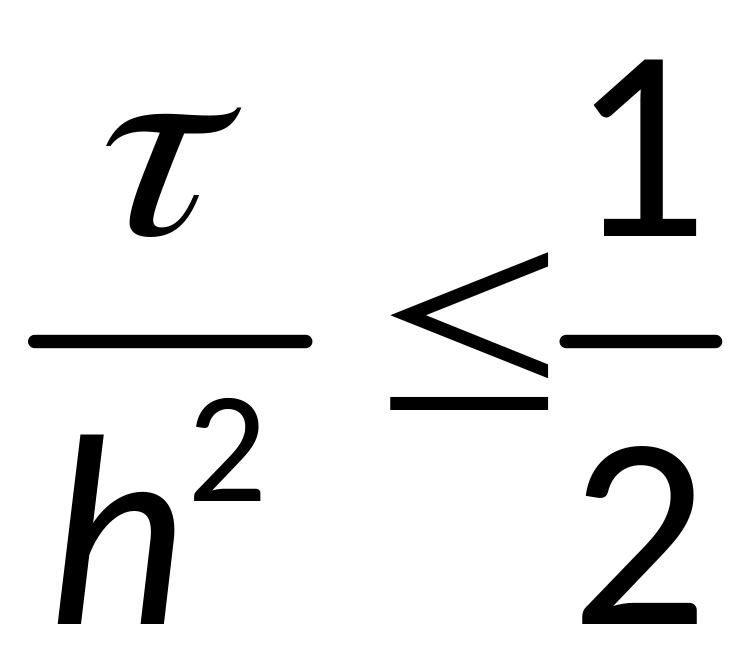- условие явной разностной схемы

34. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: неявная схема, абсолютная устойчивость неявной схемы.

(1)

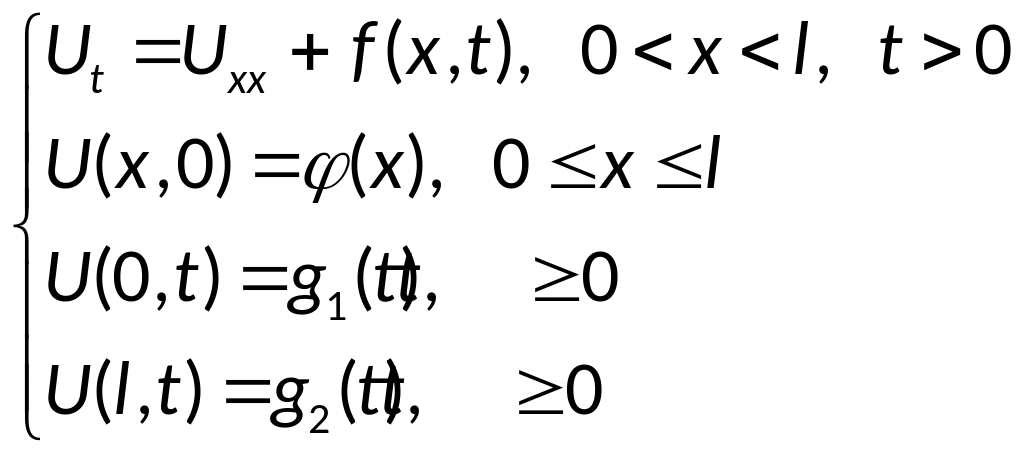
; - условия согласования

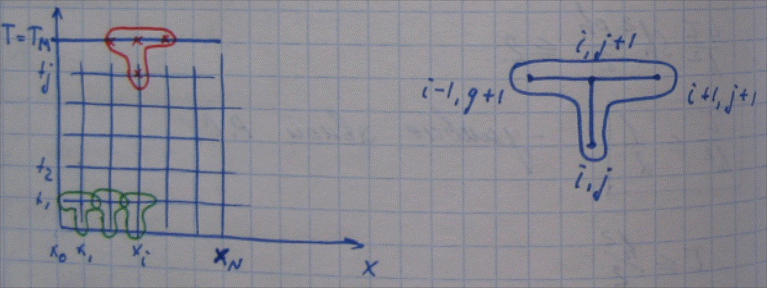
Посредством метода конечных разностей, строим неявную разностную схему:

(2)

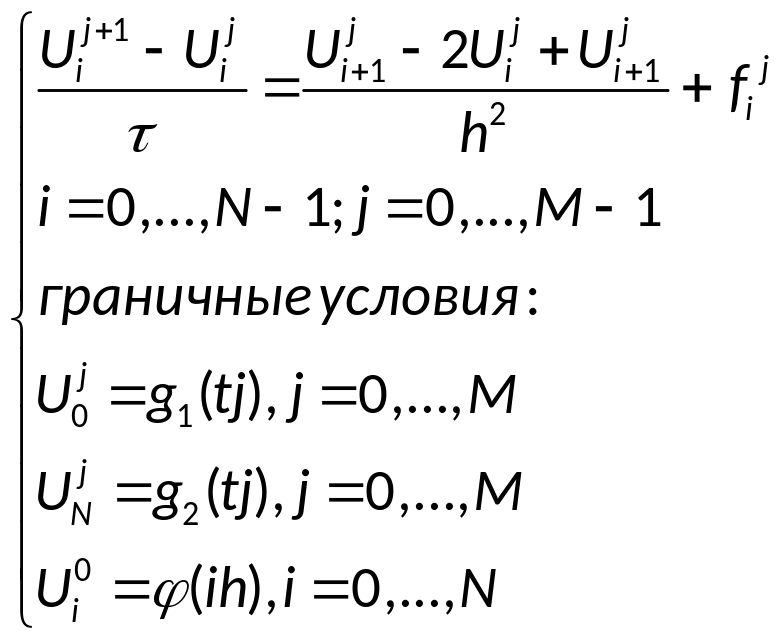
Для каждой точки напишем систему уравнений:

AU=F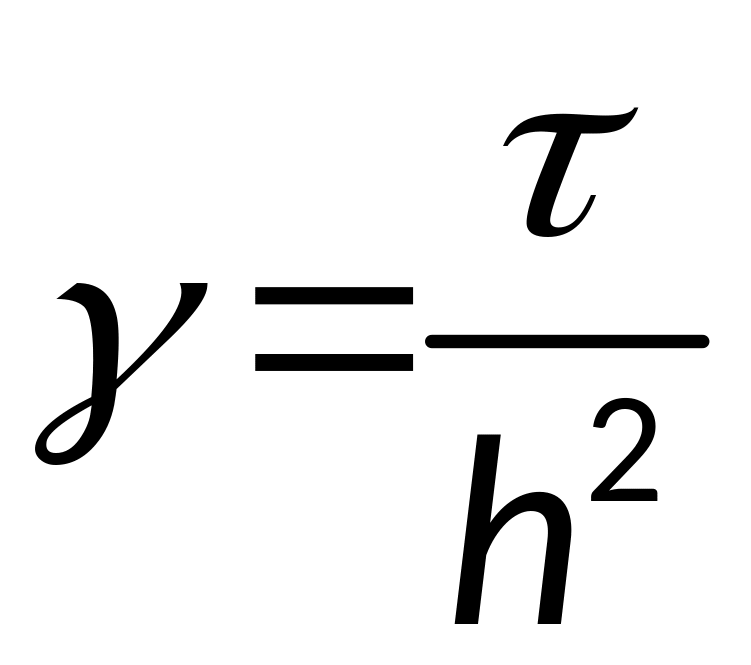

Однопараметрическое семейство разностных схем имеет вид:

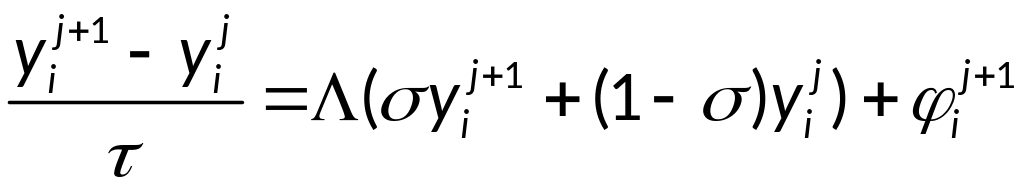, где

σ – произвольный вещественный параметр (вес верхнего слоя );

;

при σ=0 получаем явную разностную схему;

при σ≠0 получаем неявную разностную схему;

Рассмотрим неявную разностную схему при σ=1

и выпишем СЛАУ в традиционном виде:

Алгоритм решения задачи:

1. Решением задачи является

2. Первоначально заполняются начальный слой и граничные слои

3. Для каждого слоя j будем формировать правую часть F.

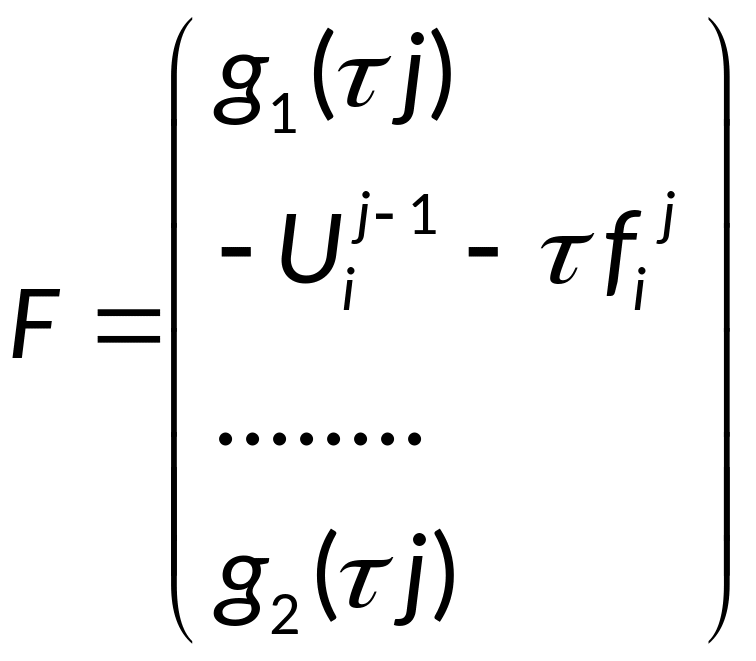
4. Решаем систему Ay=F

5. Обработка результатов

- исследование сходимости

- построение графиков

Аналитическое решение имеет вид:

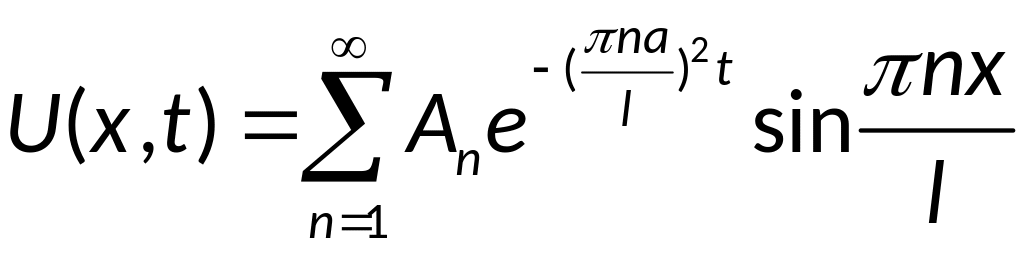, где A_n находится в виде:

Доказательство устойчивости неявной разностной схемы:

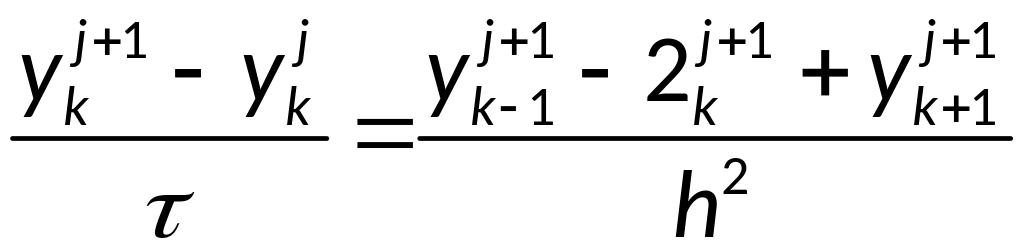
, - схема неустойчива

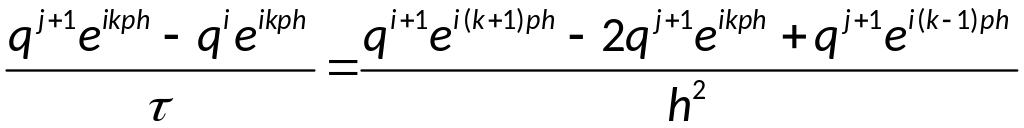
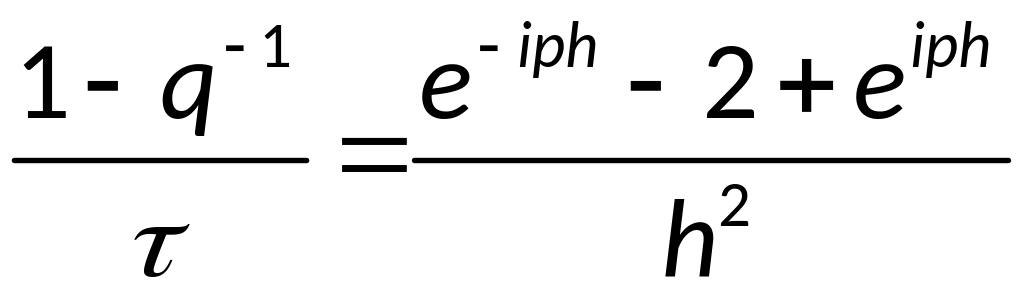
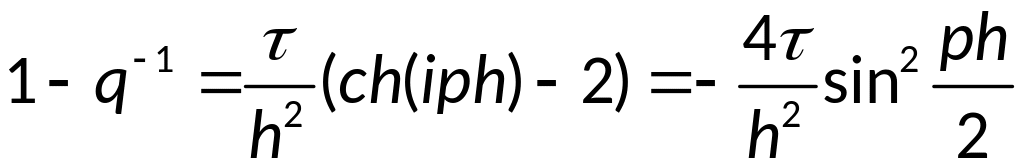
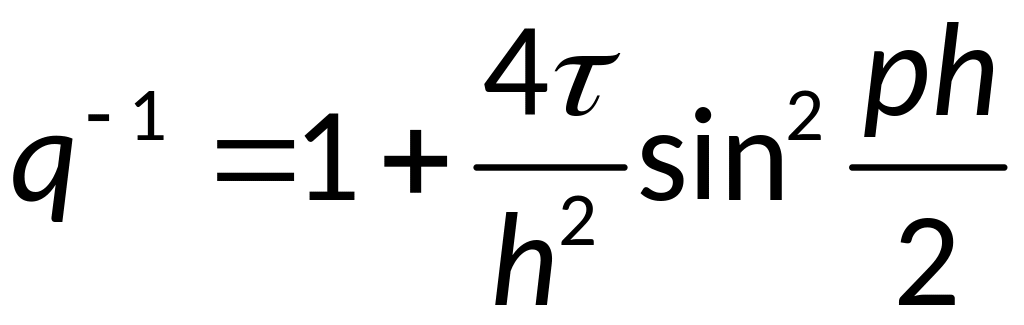
, схема является абсолютно устойчивой

35.Метод переменных направлений решения двумерной начально-краевой задачи для уравнений теплопроводности.

Будем рассматривать поставленную задачу – нагревание мембраны:

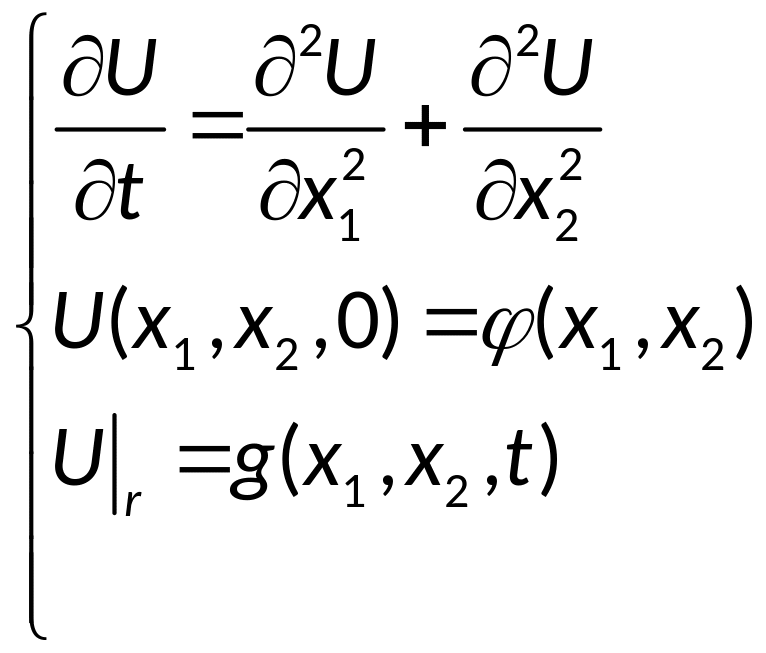
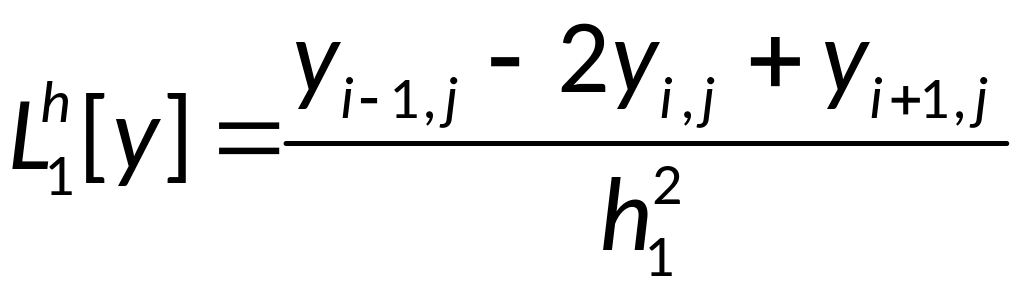- разностный оператор

Операторная запись разностной схемы:

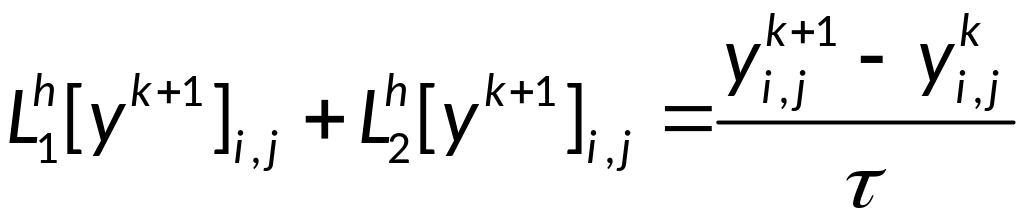
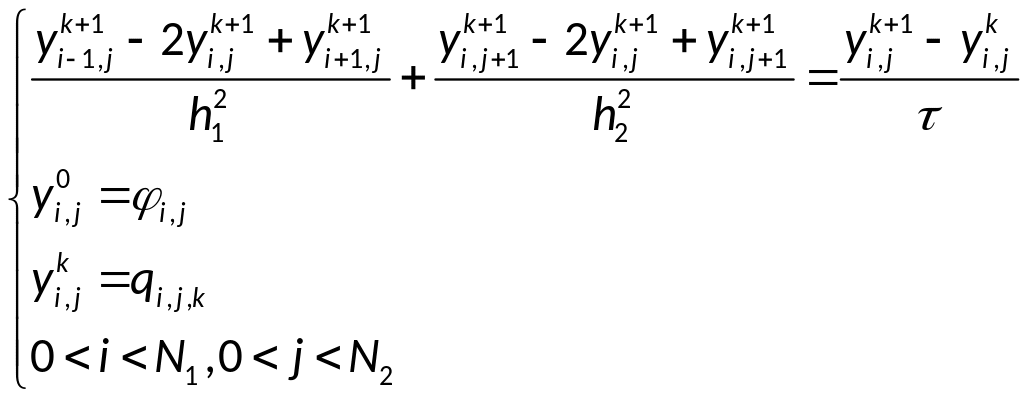
Будем реализовывать разностную схему в два этапа, введя половинный слой по времени:

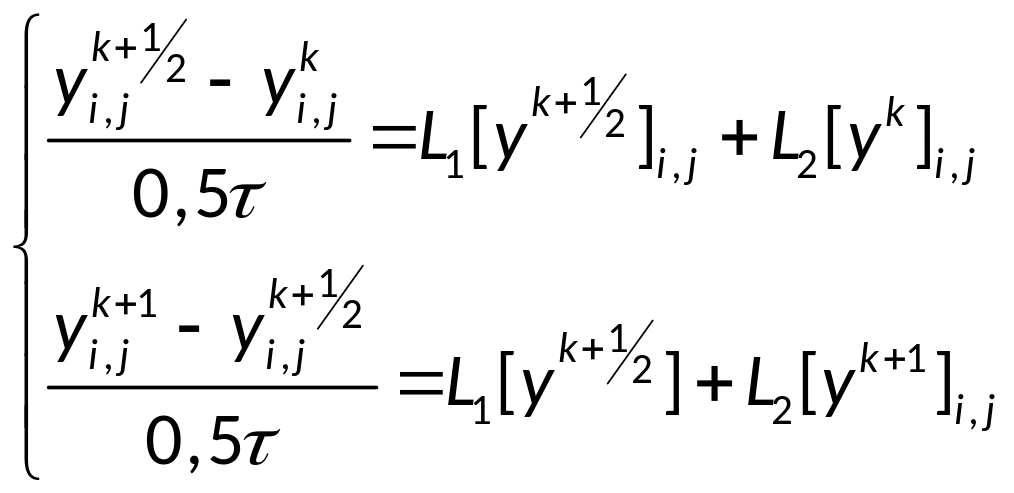
Первое уравнение:

При каждом фиксированном j выполняется прогонка по направлению x₁. Общее число арифметическиех действий

Разностные схемы в которых число арифметических действий N равно числу узлов на слое – называются экономичными. Метод переменных направлений является экономичной разностной схемой.

Другой способ решения этой задачи – применение локально-одномерных задач.

Локально-одномерная схема (трёхмерная и большее число пространственных измерений)

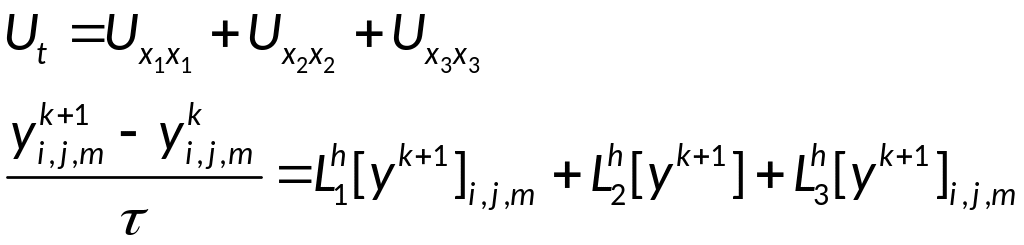
Локально-одномерная схема:

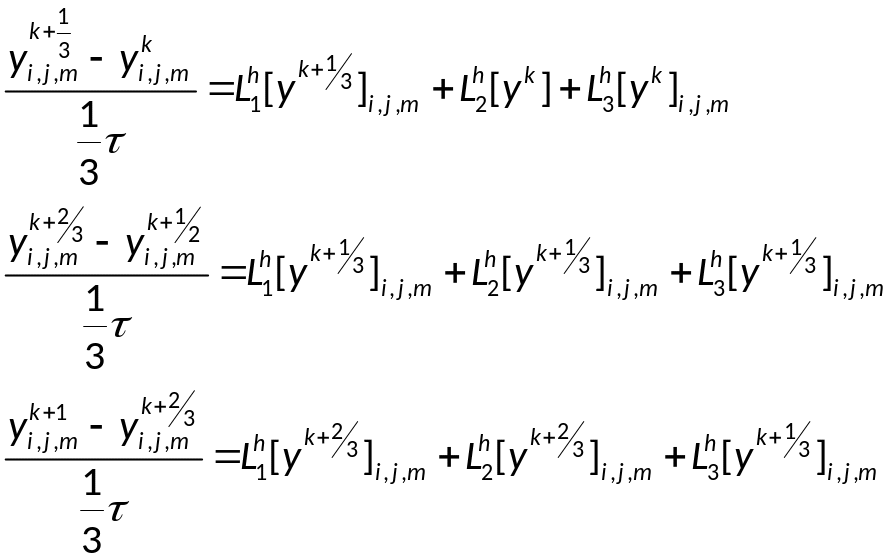
36. Метод конечных разностей решения начально-краевой задачи для уравнения колебаний струны: схема крест, порядок аппроксимации.

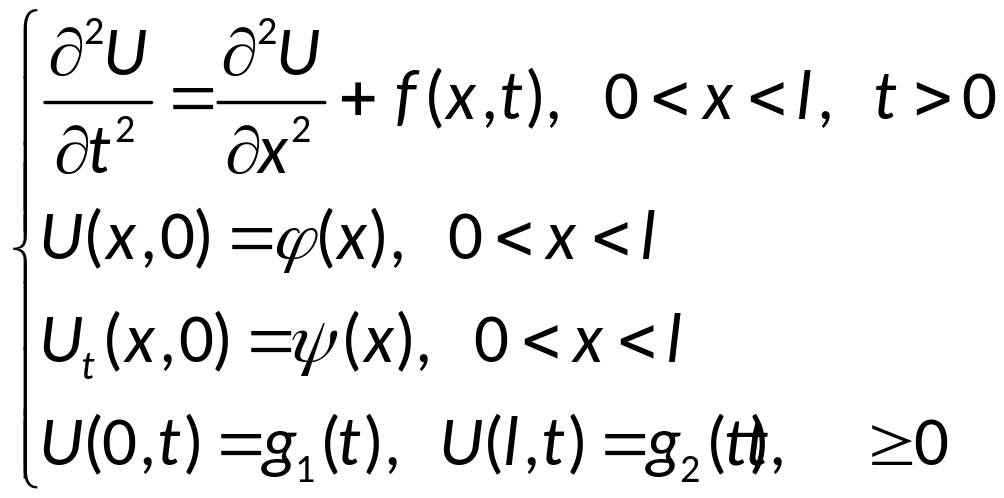
Условие согласования:

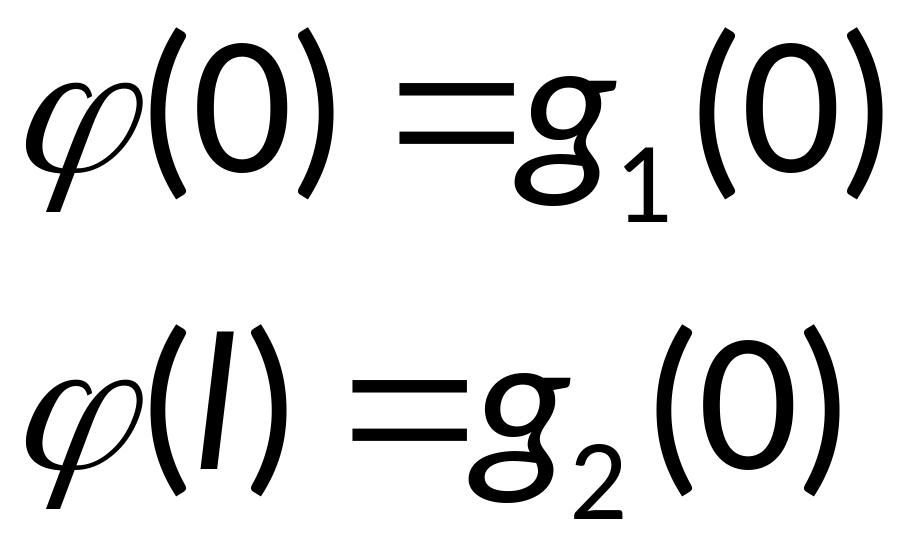
Это уравнение написано на пяти-точечном шаблоне. Необходимо вычислить значения на слое Очевидно, что находится из условия

находим из условия

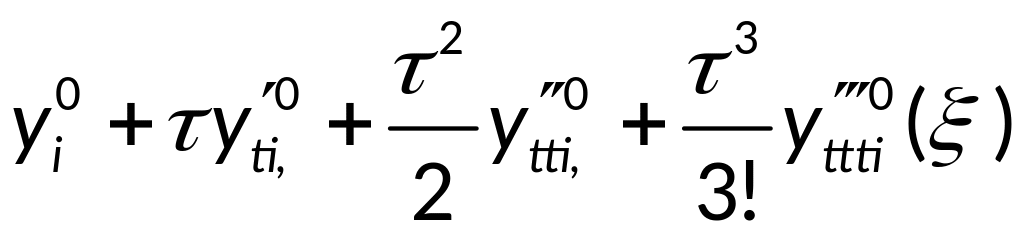
Тогда аппроксимация примет вид:

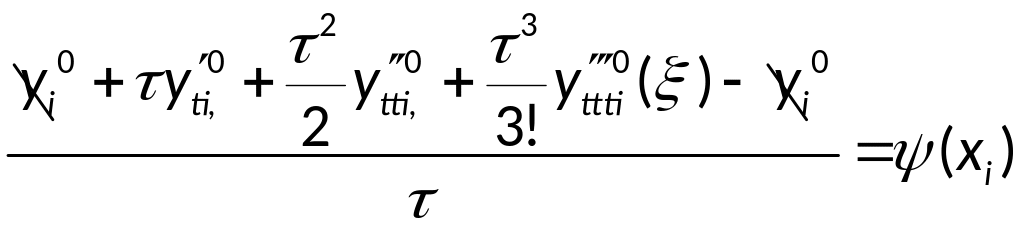
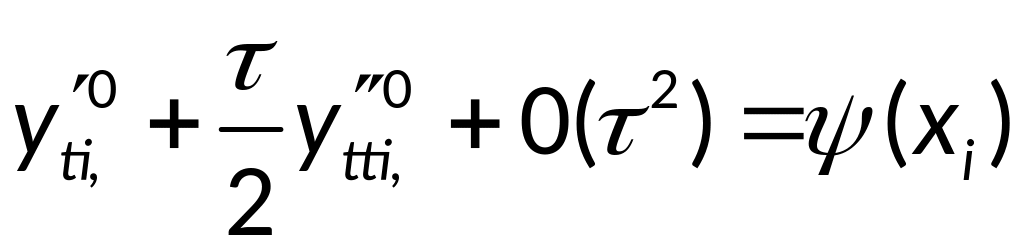
Алгоритм и разностная схема для уравнения колебаний:

1.

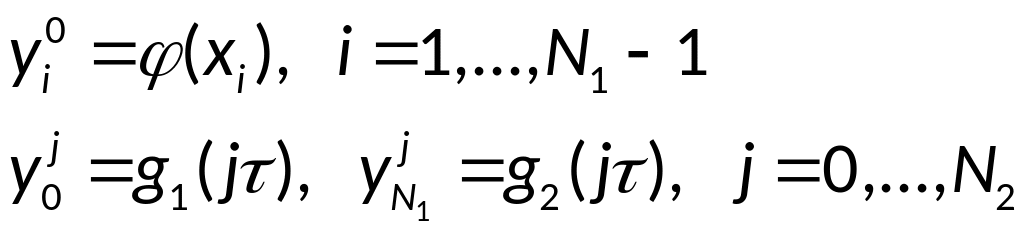
2. Значения на первом слое:

3.

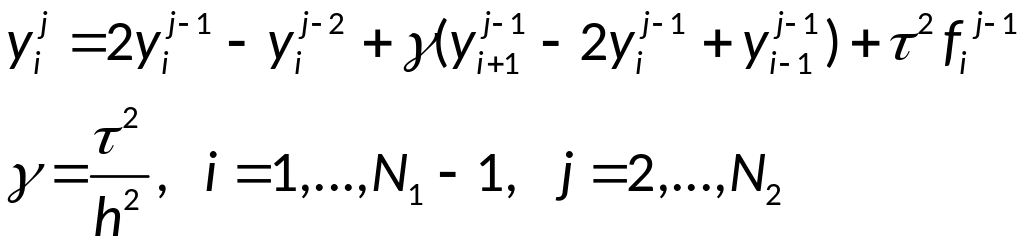
37.Метод конечных разностей решения начально-краевой задачи для уравнения колебаний струны: условная устойчивость схемы.

Докажем, что схема является условно-устойчивой, методом гармоник:

для этого рассмотрим разностную схему для одного уравнения:

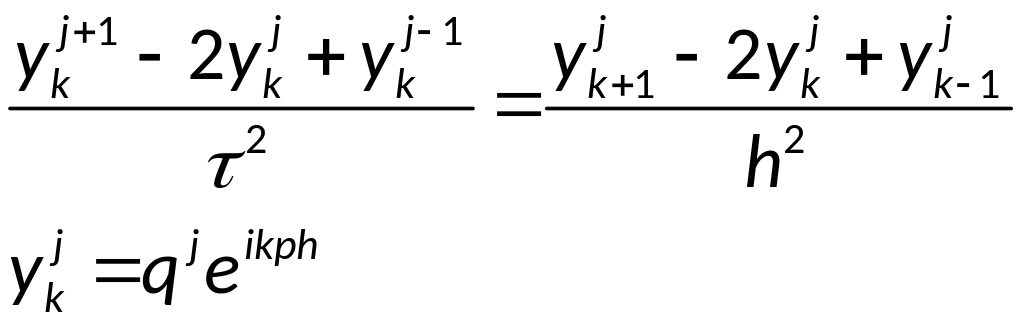
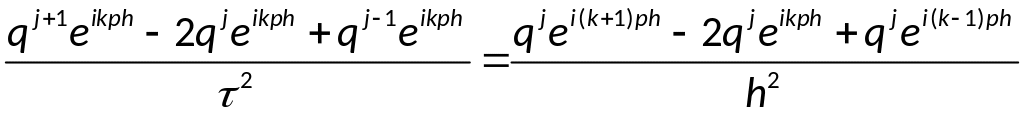
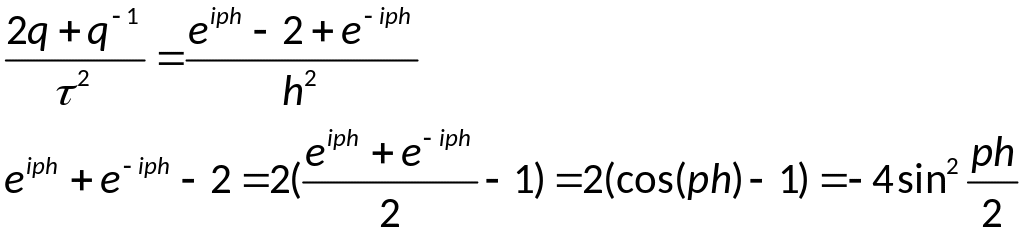
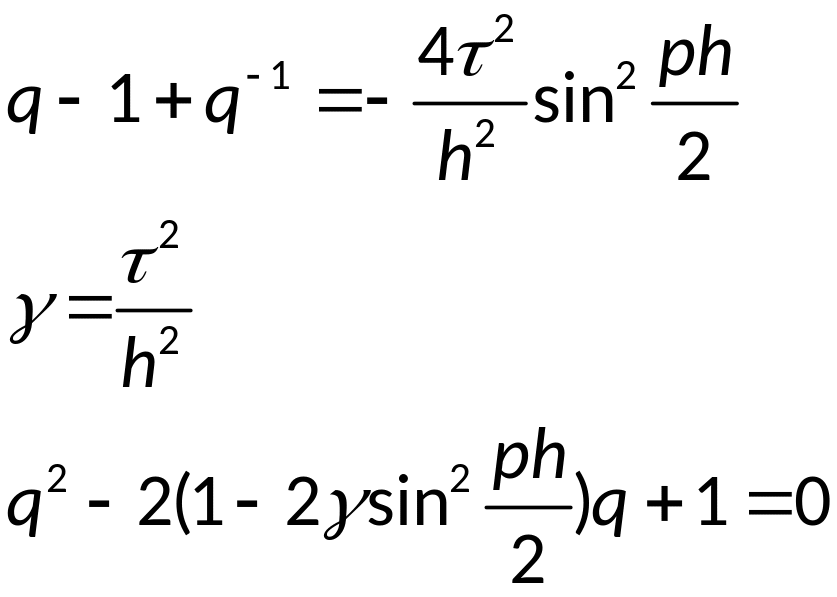
По теореме Виета:

38. Метод конечных разностей решения задачи Дирихле для уравнения Пуассона. Порядок аппроксимации схемы.

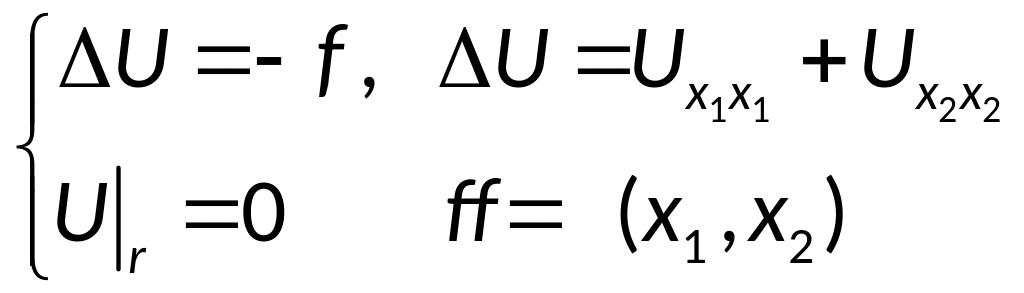
Разностная схема выглядит следующим образом:

Разностное уравнение – аппроксимация исходного дифференциального уравнения:

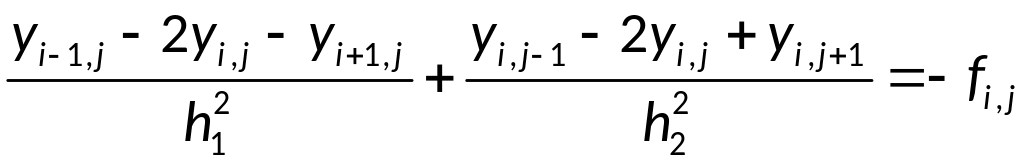
Дальнейшее разложение элементов уравнения в ряд Тейлора даст нам искомый порядок аппроксимации (будем рассматривать случай ).

39. Метод конечных разностей решения задачи Дирихле для уравнения Пуассона. Итерационные методы решения сеточных уравнений: простой итерации.

Задача Дирихле для уравнения Пуассона определяется, как задача нахождения , удовлетворяющей в области определения D уравнению:

и (f и g задаются в задаче). Подобная модель может применяться для описания установившегося течения жидкости, стационарных тепловых полей, процессов теплопередачи с внутренними источниками тепла и деформации упругих пластин.

Одним из наиболее распространенных подходов к численному решению дифференциальных уравнений является метод конечных разностей (метод сеток). Следуя этому подходу, область решения D можно представить в виде дискретного (как правило, равномерного) набора (сетки) точек (узлов). Так, например, прямоугольная сетка в области D может быть задана в виде пятиточечного шаблона.

Разностная схема выглядит следующим образом:

Разностное уравнение-аппроксимация исходного дифференциального уравнения:

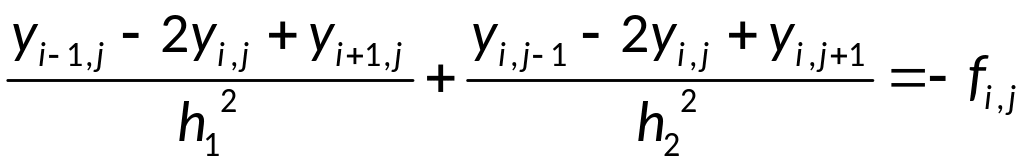
Простой итерации:

Расчетная формула метода простой итерации: